Diabolique

° Carré diabolique. – Nom donné par Édouard Lucas (1842-1891) à un carré magique d'ordre n ayant une propriété additionnelle, c'est-à-dire que la somme des n nombres de chaque diagonale brisée est aussi égale à la densité. Un tel carré demeure magique quand on permute les rectangles obtenus en le coupant par une droite parallèle aux côtés. Le seul carré magique normal d'ordre 3 n'est pas diabolique. 

Il existe 48 carrés diaboliques normaux d'ordre 4. On peut partager ces carrés en trois classes de 16 carrés chacun en tenant compte du fait que chaque rangée de quatre éléments est composée ou non d’un élément de chacun des quatre quadruplets : (1, 2, 3, 4), (5, 6, 7, 8), (9, 10, 11, 12), (13, 14, 15, 16).

La liste des carrés diaboliques est donnée ci-dessous et partagée en trois classes. Les numéros sont ceux attribués par Frénicle.

Ö Classe 1

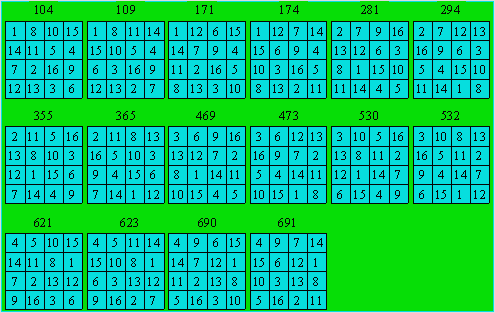
On retrouve les mêmes rangées dans des positions différentes. Par exemple, huit carrés ont le quadruplet (1, 8, 10, 15) sur une ligne ou dans une colonne. De même, huit carrés ont le quadruplet (1, 8, 11, 14) sur une ligne ou dans une colonne.

Ö Classe 2

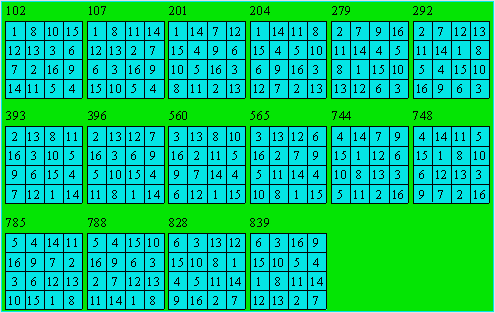
Les six premiers carrés ont une diagonale (1, 4, 13, 16), les quatre suivants (2, 3, 14, 15), les six derniers (5, 8, 9, 12).

Ö Classe 3

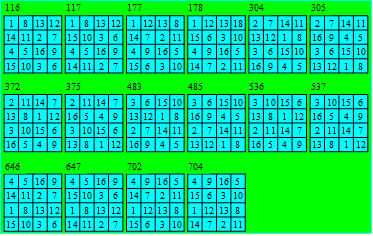
Les lignes de chaque carré contiennent les quadruplets suivants : (1, 8, 12, 13), (2, 7, 11, 14), (3, 6, 10, 15), (4, 5, 9, 16). Le troisième quadruplet est formé par quatre nombres triangulaires successifs ; le quatrième a trois carrés successifs. Les colonnes contiennent : (1, 4, 14, 15), (2, 3, 13, 16), (5, 8, 10, 11), (6, 7, 9, 12).

Il existe 3 600 carrés diaboliques d'ordre 5, aucun d'ordre 6 et 38 102 400 d'ordre 7, sans compter dans chacun des cas les carrés obtenus par rotation ou par symétrie. Il n'y a pas de carré diabolique d'ordre impairement pair, c'est-à-dire d'ordre (4n + 2). 

Les 3600 carrés diaboliques d'ordre 5 peuvent être formés à partir d'un seul carré de base illustré à gauche ci-dessous. Les majuscules peuvent prendre les valeurs 1, 2, 3, 4 et 5 ; les minuscules, 0, 5, 10, 15 et 20 ou inversement. Un carré diabolique d'ordre 5 est illustré à droite. Dans ce cas, A = 0, B = 15, C = 5, D = 20, E = 10, a = 3, b = 5, c = 2, d = 4 et e = 1.

Dans un carré diabolique normal d'ordre 5, la somme des éléments de chacune des huit diagonales brisées est égale à 65. Au total, il y a 20 rangées de même somme. Dans le carré de base, les lettres peuvent être permutées pour permettre d'autres carrés équivalents. 

Cet algorithme de construction de carrés diabolique peut s'appliquer à tous les carrés d'ordre impair avec des adaptations lorsque n n'est pas premier. Lorsque n est égal à 7, il existe six carrés de base. La disposition de nombres dans un carré diabolique a permis d'établir le principe arithmétique de la géométrie du tissage. 

Un carré magique d'ordre n est dit semi-diabolique lorsque la somme des n nombres d’au moins une et au plus (n - 1) diagonales brisées par rapport à chacune des deux diagonales principales est égale à la densité. 

Un carré magique n'étant ni diabolique ni semi-diabolique est dit simple. 

© Charles-É. Jean