|
|
|
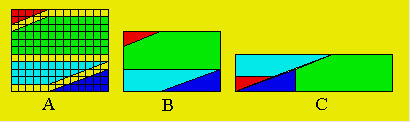
° Rectangle de Langman. – Ensemble de quatre pièces créé par Langman qui, une fois assemblées, peuvent former un rectangle 8 ×13. Les pièces sont représentées en A et le rectangle en B. L’aire de ce rectangle est de 104 unités carrées. En agençant les pièces comme en C, un rectangle 5 × 21 peut être formé. L’aire de ce rectangle semble être de 105 unités carrées. Le long de la droite oblique, il y a une perte d’une unité carrée : ce qui explique l’excès d’une unité carrée dans le rectangle de droite.
Ce phénomène se produit quand les mesures des côtés des polygones sont des nombres de Fibonacci. Les côtés de l’angle droit des deux triangles sont 2 et 5, puis 3 et 8. Les côtés de l’angle droit du pentagone sont 8, 5 et 13 et ceux du quadrilatère 13, 3 et 5. Le rectangle de Langman appartient à la classe des récréations de construction. Voir aussi : Carré de Curry, Rectangle de Curry, Rectangle de Hooper, Triangle de Curry © Charles-É. Jean
|
