|
Pentagonal
°
Nombre gnomonique
pentagonal. – Nombre qui est représenté par le gnomon
d'un
pentagone régulier. Tout nombre de rang n de cette classe, en excluant
1, est un multiple de 3 auquel on additionne 1. Le terme général est (3n
- 2).
Les quatre plus petits gnomoniques pentagonaux peuvent être représentés
ainsi :
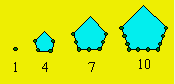
Un nombre est un gnomonique pentagonal si, lui ayant
soustrait 1 et ayant divisé le résultat par 3, le quotient est un entier. Son
rang est le quotient augmenté de 1. Pour trouver son successeur, on additionne
3 au nombre. Par exemple, 52 est un gnomonique pentagonal car (52 - 1)/3 = 17.
Son rang est 18. Son successeur est 55. Les 29 plus petits gnomoniques
pentagonaux sont :
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
0 |
|
1 |
4 |
7 |
10 |
13 |
16 |
19 |
22 |
25 |
|
1 |
28 |
31 |
34 |
37 |
40 |
43 |
46 |
49 |
52 |
55 |
|
2 |
58 |
61 |
64 |
67 |
70 |
73 |
76 |
79 |
82 |
85 |
Voici quelques
propriétés concernant les nombres de cette classe :
La période des unités des nombres successifs correspond à un nombre de 10 chiffres
différents : 1 470 369 258. La somme des chiffres de mêmes rangs
extrêmes est 9.
La somme des n premiers gnomoniques pentagonaux est un pentagonal
de rang
n.
Tout gnomonique pentagonal est la différence de deux pentagonaux successifs.
L’ensemble des gnomoniques pentagonaux forme une suite arithmétique de degré
1.
Les gnomoniques pentagonaux sont des
nombres figurés.
© Charles-É. Jean
Index
: P
|
![]()
![]()