° Nombre trapézoïdal. – Nombre plan ou de dimension 2 qui est représenté par un trapèze isocèle. Ce nombre correspond à la somme d’entiers consécutifs. À l'encontre des polygonaux associés à des figures régulières, un trapézoïdal peut avoir plus d'une représentation. Le degré d'un trapézoïdal est le nombre de représentations qui lui est associé. Ainsi, 30 est un trapézoïdal de degré 3, car il a trois représentations :

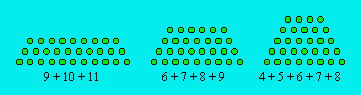
Tous les entiers, sauf 2 et les puissances entières de 2, sont des trapézoïdaux. Voici trois façons de reconnaître le degré d’un trapézoïdal :

1. Tout nombre premier impair, de même que ses multiples purement pairs, sont des trapézoïdaux de degré 1. Les 10 plus petits trapézoïdaux de degré 1 sont : 1, 3, 5, 6, 7, 10, 11, 12, 13 et 14.

2. Tout carré d'un nombre premier impair, de même que ses multiples purement pairs, sont des trapézoïdaux de degré 2. Les 10 plus petits trapézoïdaux de degré 2 sont : 9, 18, 25, 36, 49, 50, 72, 98, 100 et 121.

3. Tout cube d'un nombre premier impair et tout entier formé par le produit de deux nombres premiers impairs différents, de même que leurs multiples respectifs purement pairs, sont des trapézoïdaux de degré 3. Les 10 plus petits trapézoïdaux de degré 3 sont : 15, 21, 27, 30, 33, 35, 39, 42, 51 et 54.

Voici le plus petit nombre qui est trapézoïdal pour chaque degré de 4 à 14 :

Certaines classes de nombres figurés correspondent à des trapézoïdaux. Par exemple, les pentagonaux peuvent être représentés ainsi :

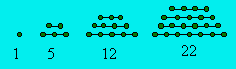
Le nombre de lignes de points est égal au rang n du terme ; le nombre de points de la base est (2n - 1). Les trapézoïdaux sont des nombres figurés.

© Charles-É. Jean

Index : T

Pour en savoir plus, lisez l'article Les nombres trapézoïdaux.