Les nombres figurés
Un nombre figuré est le cardinal d'un ensemble de points, lesquels sont arrangés de façon régulière en une figure géométrique. Des points disposés en ligne droite forment un nombre linéaire, si bien que tout entier est linéaire.

Un ensemble de points disposés de façon régulière en un polygone régulier convexe représente un nombre polygonal. Citons les nombres triangulaires, carrés, pentagonaux, hexagonaux, que nous illustrons par un exemple.

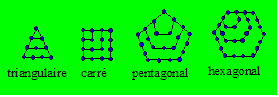
Les polygones convexes non réguliers ont été l'objet de peu d'attention. En particulier, la classe des nombres rectangulaires a été définie par rapport aux nombres oblongs ou hétéromèques (1). Ceux-ci correspondent à un ensemble de points disposés en un rectangle dont un côté mesure une unité de plus que l'autre. La suite des oblongs ou hétéromèques est 2, 6, 12, 20, 30, 42, etc.

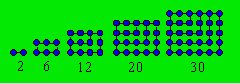
Il existe également des classes de nombres figurés à trois dimensions. Mentionnons les cubiques et les pyramidaux qui peuvent être classés selon la forme de la base de leur pyramide. En particulier, Albert H. Beiler (2) et Maurice Kraitchik (3) ont étudié les nombres de dimension supérieure à 3.

Dans le cadre de cet article, notre intention est de faire une brève présentation des nombres triangulaires et d'introduire, par la suite, une nouvelle classe : les nombres trapézoïdaux.

1. Les nombres triangulaires
Un nombre triangulaire est représenté par des lignes de points disposés en un triangle. Chaque ligne horizontale successive contient 1, 2, 3, 4, 5, etc. points. Les cinq plus petits triangulaires sont :

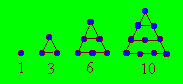
Certains auteurs présentent ces nombres ainsi :

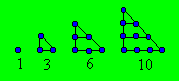
Remarquons qu'un même nombre de points apparaît sur chaque côté du triangle extérieur. Ce nombre qui est la mesure du côté est égal au rang du triangulaire dans l'ordre numérique croissant, de même qu'au nombre de lignes de points de la figure. Dans ce sens, nous pouvons considérer le triangle comme équilatéral.

Nous pouvons également représenter les triangulaires par des carrés, des cercles ou des boules linéaires. En adoptant ces formes sur un plan, il est possible alors de faire de la manipulation. Voici le triangulaire 15 au moyen de carrés et de boules :

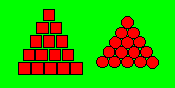
Tout triangulaire est constitué, à partir du précédent, par l'ajout d'une ligne de points ou de boules dont le nombre est égal à son rang. Sous son aspect arithmétique, tout triangulaire est formé par la somme des entiers consécutifs à partir de l'unité.

1 = 1     3 = 1 + 2     6 = 1 + 2 + 3     10 = 1 + 2 + 3 + 4    15 = 1 + 2 + 3 + 4 + 5

Ces entiers forment une progression arithmétique de raison 1 dont le nombre de termes est égal au dernier. En appliquant la formule de la somme des termes d'une progression arithmétique, nous pouvons identifier le triangulaire t de tout rang n.

[1]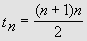 

Huit figures d'un même triangulaire disposées autour d'un point central forment un carré.

C'est là l'essence même d'une proposition énoncée et démontrée par Diophante (v. 325 - v. 410) dans son Arithmétique : l'octuple d'un triangulaire augmenté de l'unité est toujours un carré.

Nous pouvons en déduire que si l'expression (8z + 1), où z est un entier naturel, est un carré, alors z est triangulaire. Son rang n est :

[2]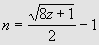

Par exemple, 666 est un triangulaire car : (8 × 666) + 1 = 5329 = 73². Son rang est égal à (73 - 1)/2 = 36. D'où, 666 est le 36^e triangulaire.

2. Notion d'un nombre trapézoïdal
Cette brève présentation des triangulaires nous amène à étudier une nouvelle classe de nombres que nous appellerons trapézoïdaux, puisque la figure formée de points a la forme d'un trapèze. Les points sont disposés de façon régulière comme dans un triangulaire et chaque ligne contient un point de plus que la ligne supérieure, également comme dans un triangulaire.

Prenons une figure illustrant le triangulaire 21 et retenons l’ensemble des boules vertes, comme il est illustré. Nous obtenons le trapézoïdal 12.

Un nombre trapézoïdal est le cardinal d'un ensemble de points ou de boules, lesquels sont disposés en lignes parallèles contenant successivement un point ou une boule de plus que la ligne supérieure. Lorsque la ligne du sommet contient un point ou une boule, le nombre est aussi triangulaire. Nous considérons donc les trapézoïdaux comme un sous-ensemble des triangulaires. Sous sa forme arithmétique, un trapézoïdal est la somme d'entiers consécutifs à partir de n'importe lequel entier.

Tout nombre triangulaire possède une figure unique. Toutefois, les trapézoïdaux peuvent accepter plus d'une représentation. Voici, à titre d'exemples, les trois figures du trapézoïdal 30 :

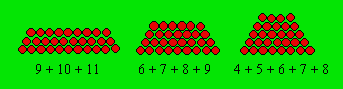
Si nous complétons dans leur partie supérieure chacune de ces figures par des lignes de boules ayant successivement une boule de moins jusqu'à l'unité, la partie ajoutée formera un triangulaire de même que la figure complète.

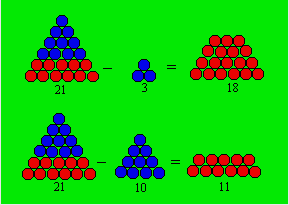
Inversement, en coupant la partie supérieure d'un triangulaire parallèlement à la base de telle façon qu'il reste plus d'une ligne de boules, nous obtenons un trapézoïdal. Le triangulaire 21, auquel on retranche 3 ou 10, deux autres triangulaires, donne une représentation des trapézoïdaux 18 et 11.

3. Identification des nombres trapézoïdaux
Nous allons montrer que tous les entiers, sauf 2 et les puissances entières de 2, sont des trapézoïdaux.

Nous savons qu'un trapézoïdal est la somme d'entiers consécutifs. Appelons a le plus petit entier et b le nombre de termes de la suite. La somme des termes qui correspond au trapézoïdal T pourra s'écrire ainsi :

[3]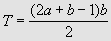   

Construisons la table des trapézoïdaux en fonction des valeurs de a et de b.

Faisons une brève analyse de ce tableau. Lorsque b est égal à 2, le trapézoïdal est de la forme (2a + 1). Les multiples consécutifs de (2a + 1) apparaissent dans les autres rangées horizontales suivant une régularité que nous allons décrire. Par exemple, les multiples de T(5, 2) = 11 sont : T(4, 4) = 22, T(3, 6) = 33, T(2, 8) = 44, T(1, 10) = 55, T(1, 11) = 66, T(2, 11) = 77, T(3, 11) = 88, etc.

Nous observons que le passage d'un multiple à l'autre jusqu'à 55 s'effectue selon le saut classique du cavalier aux échecs c'est-à-dire que a diminue successivement d'une unité tandis que b augmente de 2. Par ailleurs, 66 est dans la même colonne que 55, mais sur la ligne immédiatement inférieure. Les autres multiples de 11 à partir de 66 sont dans la même ligne que 66, là où a est égal à 11.

Nous pouvons généraliser cette situation en énonçant trois propositions :

Lemme 1. Les multiples du trapézoïdal T(a, 2), où a est plus grand que 2, apparaissent de façon consécutive selon le saut du cavalier, jusqu'à ce que a soit égal à 1.

Posons a = p et b = 2q, où p et q sont des entiers naturels, dans l'équation [3].
T₁ = (2p + 2q - 1)q

Posons a = p - 1 et b = 2q + 2.
T₂ = (2p + 2q - 1)(q + 1)

Lorsque a diminue de 1 et que b augmente de 2, tout nombre et son successeur, repérés dans la table, ont (2p + 2q -1) comme facteur commun. Ces nombres sont des multiples consécutifs de T(a, 2) jusqu'à T(1, 2a) qui est égal au produit de a et de T(a, 2).

Lemme 2. Les trapézoïdaux T(1, 2a) et T(1, 2a + 1) sont deux multiples consécutifs de T(a, 2). En effet, T(1, 2a) = (2a + 1)a et T(1, 2a + 1) = (2a + 1)(a + 1). Par ailleurs, T(a, 2) = (2a + 1).

Lemme 3. Tous les trapézoïdaux d'une même rangée horizontale sont des multiples consécutifs de b, lorsque b est impair. En effet, tout nombre d'une même ligne, d'après la formule [3], est égal à : .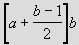 

Comme b conserve toujours la même valeur et que a augmenté successivement d'une unité, les multiples de b sont consécutifs à partir de (b + 1)b/2.

D'après les lemmes 1 et 2, les multiples de T(a, 2) apparaissent de façon consécutive jusqu'à ce que a soit égal à 1 et que b soit égal à (2a + 1). D'après le lemme 3, à partir de T(1, 2a + 1), les autres multiples consécutifs apparaissent tous dans une même rangée horizontale. Nous pouvons donc affirmer que tous les multiples de tout entier impair à partir de 3 se trouvent dans la table. En conséquence, tous les entiers impairs et les multiples pairs de ces entiers y apparaissent au moins une fois.

Il nous reste à vérifier si 2 et les puissances entières de 2 peuvent se retrouver dans la table. De par la formule [3], quelle que soit la parité de a, si b est pair, alors (2a + b - 1) est impair. Par ailleurs, si b est impair, alors (2a + b - 1) est pair. L'un des deux facteurs est donc pair et l'autre impair. Or, 2 et les puissances entières de 2 n'ont que des facteurs pairs, si on excepte 1. D'où, 2, 4, 8, 16, 32, ... n'apparaissent pas dans la table.

En conséquence, tous les entiers, sauf 2 et les puissances entières de 2, sont des trapézoïdaux.

4. Recherche des figures d'un trapézoïdal
D'après la formule [3], un trapézoïdal est égal au produit de deux facteurs : (2a + b - 1) et b/2 si b est pair. Il est égal au produit de (2a + b - 1)/2 et de b si b est impair. Transformons la formule en fonction de a.

[4]   

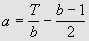
4.1 Considérons d'abord le cas où b est impair.

La plus petite valeur possible de a est l'unité. En remplaçant a par 1 dans la formule [4] et en résolvant l'équation obtenue, nous pouvons identifier la plus grande valeur de b que nous appellerons la limite.

[5]   

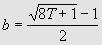
Chaque diviseur de T, sauf 1, inférieur ou égal à la limite, engendre donc une figure trapézoïdale.

Soit le trapézoïdal 33. Les diviseurs sont 1, 3, 11 et 33. Selon la formule [5], la plus grande valeur de b est 7,639... Parmi les diviseurs de 33, seul 3 peut être retenu. Si b est égal à 3, alors a est égal à 10. La figure est T(10, 3).

4.2 Considérons le cas où b est pair.

En somme, sauf 1, chaque diviseur d'un trapézoïdal, inférieur à la limite obtenue, engendre une figure trapézoïdale. De même, chaque double d'un diviseur d'un trapézoïdal, qui respecte cette limite, permet une figure trapézoïdale.

5. Degré d'un trapézoïdal
Le degré d'un trapézoïdal est le nombre de figures qui lui est associé. Nous allons tenter de trouver une formule qui permettra de calculer le degré d'un trapézoïdal sans connaître ses représentations. Le tableau des trapézoïdaux donné précédemment va nous aider dans ce sens.

Comme nous l'avons expliqué, nous y trouvons successivement les multiples des impairs consécutifs à partir de 3. En conséquence, tout trapézoïdal apparaîtra dans la table autant de fois qu'il est un multiple d'un entier impair. Nous devons donc compter le nombre de diviseurs impairs d'un trapézoïdal et soustraire ce nombre d'une unité, étant donné que 1 est exclu. Ainsi, 45 a six diviseurs impairs : 1, 3, 5, 9, 15 et 45. Son degré est 5. Par ailleurs, 36 a trois diviseurs impairs : 1, 3 et 9. Son degré est 2.

La théorie des nombres nous apprend que si aⁱ.b^j.c^k... est la factorisation en nombres premiers d'un entier positif, alors le nombre de diviseurs positifs de cet entier est : (i + 1)(j + 1)(k + 1)... Or, un entier impair n'a que des diviseurs impairs. En conséquence, le degré d'un trapézoïdal impair est : (i + 1)(j + 1)(k + 1)... - 1.

Par ailleurs, le nombre de diviseurs impairs d'un entier pair est aussi égal à (i + 1)(j + 1)(k + 1) ... où i, j, k sont les exposants des nombres premiers supérieurs à 2. Ainsi, les trapézoïdaux k et 2ⁿ.k, où n est un entier naturel, sont de même degré.

En résumé, tout nombre de la forme 2ⁿ.aⁱ.b^j.c^k ... est un trapézoïdal de degré (i + 1)(j + 1)(k + 1) ... - 1 , lorsque a, b, c, ... sont des nombres premiers supérieurs à 2 et que i, j, k, ..., n sont des entiers naturels. Cherchons le degré de 396. Sa factorisation en nombres premiers est : 2² × 3² × 11. Le degré est (2 + 1)(1 + 1) - 1 = 5.

Dans les propositions suivantes, l'expression purement pair fait référence à 2 et aux puissances entières de 2. Par exemple, 9 est un trapézoïdal de degré 2. Les nombres 18, 36, 72, 144, ... sont aussi de degré 2. On a 9 × 2, 9 × 4, 9 × 8, 9 × 16, ...

Proposition 1. Tout nombre premier impair, de même que ses multiples purement pairs, sont des trapézoïdaux de degré 1. Réciproquement, tout trapézoïdal impair de degré 1 est un nombre premier. Les dix plus petits trapézoïdaux de degré 1 sont : 1, 3, 5, 6, 7, 10, 11, 12, 13 et 14.

Proposition 2. Tout carré d'un nombre premier impair, de même que ses multiples purement pairs, sont des trapézoïdaux de degré 2. Les dix plus petits trapézoïdaux de degré 2 sont : 9, 18, 25, 36, 49, 50, 72, 98, 100 et 121.

Proposition 3. Tout cube d'un nombre premier impair et tout entier formé par le produit de deux nombres premiers impairs différents, de même que leurs multiples purement pairs respectifs, sont des trapézoïdaux de degré 3. Les dix plus petits trapézoïdaux de degré 3 sont : 15, 21, 27, 30, 33, 35, 39, 42, 51 et 54.

Proposition 4. Toute quatrième puissance d'un nombre premier impair, de même que ses multiples purement pairs, sont des trapézoïdaux de degré 4. Les dix plus petits trapézoïdaux de degré 4 sont : 81, 162, 324, 625, 648, 1250, 1296, 2401, 2500 et 2592.

Proposition 5. Plus généralement, tout nombre premier impair élevé à une puissance entière n, de même que leurs multiples purement pairs, sont des trapézoïdaux de degré n.

Proposition 6. Plus généralement, tout nombre de la forme 2ⁿ.aⁱ.b^j.c^k ... où a, b, c, ... sont des nombres premiers impairs différents et où i, j, k, ... et n sont des entiers naturels, sont des trapézoïdaux de degré (i + 1)(j + 1)(k + 1) ... - 1.

Voici deux tableaux contenant, pour chaque degré inférieur à 21, le plus petit trapézoïdal :

Propriétés et recherche
La considération des nombres trapézoïdaux nous permet de cerner davantage les propriétés des sommes d'entiers consécutifs. Nous savons maintenant que tout entier, sauf 2 et ses puissances entières, peut s'écrire d'au moins une façon comme la somme d'entiers consécutifs. Un autre résultat intéressant est que, si un entier impair est un trapézoïdal de degré 1, il est un nombre premier. Cette propriété remarquable pourrait constituer une approche nouvelle pour établir la primalité d'un entier. Toutefois, il faudrait alors que notre démarche pour déterminer le degré d'un trapézoïdal s'appuie sur une base autre que la factorisation en nombres premiers. Si une telle autre base pouvait être trouvée, nous aurions une formule pour connaître la primalité d'un entier.

D'autres classes de nombres pourraient être définies en fonction de la somme d'entiers formant une suite arithmétique. Nous savons que les nombres carrés sont formés par la somme d'entiers consécutifs impairs à partir de l'unité. De plus, il va de soi que la somme des entiers consécutifs pairs à partir de 2 correspond au double d'un nombre triangulaire. Une des avenues serait de considérer n'importe lequel entier comme point de départ.

* * * * *

Enfin, la classe des trapézoïdaux constitue un vaste champ de recherche élémentaire. Dans ce contexte, nous présentons dix problèmes.

1. Quel est le nombre de boules nécessaires pour établir toutes les figures trapézoïdales de 1000 ?

2. Combien y a-t-il de nombres inférieurs à 1000 qui ne sont pas trapézoïdaux ?

3. Combien y a-t-il de trapézoïdaux de degré 1 inférieurs à 1000 qui sont en même temps triangulaires ?

4. Combien y a-t-il de trapézoïdaux de degré 2 inférieurs à 1000 ?

5. En considérant, comme triplets, trois entiers consécutifs qui sont trapézoïdaux, quel est le plus petit triplet de degré 3 ?

6. En considérant comme jumeaux deux entiers consécutifs, combien y a-t-il de trapézoïdaux jumeaux de degré 4 et inférieurs à 1000 ?

7. Combien y a-t-il de trapézoïdaux de degré 5 inférieurs à 1000 et dont le dernier chiffre est 5 ?

8. Quel est le plus petit trapézoïdal de degré 7 qui n'est pas divisible par 5 ?

9. Quel est le plus petit trapézoïdal de degré 100 ?

10. Quel est le deuxième plus petit trapézoïdal pour chaque degré inférieur à 21 ? Û