° Réseau unicursal. – Réseau qui peut être parcouru par un mobile passant une et une seule fois sur chaque branche. Un réseau est unicursal si tous ses sommets ou nœuds sont de degré pair ou s'il y a exactement deux nœuds de degré impair. 

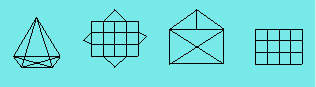
Dans le premier exemple de réseaux unicursaux ci-dessous, le mobile peut partir de n'importe quel nœud ; le point de départ coïncide avec le point d'arrivée. Dans le second cas, un nœud de degré impair constitue le point de départ, et l'autre le point d’arrivée. Ces propositions ont été énoncées et démontrées par Leonhard Euler (1707-1783) dans un mémoire sur la solution du problème des ponts de Königsberg. Les deux premiers réseaux illustrés sont unicursaux ; les deux autres ne le sont pas.

On dit que Mahomet dessinait, d'un seul coup avec la pointe de son cimeterre, sa signature formée de deux lunes opposées.

© Charles-É. Jean

Index : U-Z

Le réseau unicursal est aussi appelé réseau eulérien ou réseau économique.

Voir Récréation topologique