Solutions 1 à 10

1. Jetons de Myriam

Myriam prend huit jetons numérotés de 1 à 8. Elle doit les placer dans la grille ci-après pour que la somme soit 144. Le deuxième nombre est supérieur de 15 au premier. Le quatrième nombre est supérieur de 11 au troisième.

Distribuez les jetons.

2. Trèfles de Trefflé

Trefflé a dessiné 18 rangées de trèfles en augmentant d’un trèfle d’une rangée à l’autre. Voici les cinq premières rangées :

Combien Trefflé a-t-il dessiné de trèfles ?

3. Rêve de Jeannette

Jeannette a réalisé le rêve de sa vie.

Elle a fait un voyage d’un peu plus de trois mois en France.

Elle est partie le 28 mars et elle est revenue 102 jours plus tard.

À quelle date Jeannette est-elle revenue parmi les siens ?

4. Du pareil au même

Brigitte a pris quatre jetons et les a marqués 3.

3      3      3      3

À l’aide d’opérations simples, représentez 72 avec quatre 3.

5. Bicyclettes de Luce

Luce a dessiné trois bicyclettes sur chaque côté de la figure ci-après. Elle décide de faire un autre dessin avec 10 bicyclettes par côté.

Combien de bicyclettes Luce devra-t-elle dessiner ?

6. Égalités de François

François a préparé le tableau ci-dessous dans lequel il a écrit deux nombres et six signes.

Complétez le tableau pour qu’à la fin chacun des nombres de 1 à 9 y apparaisse.

7. Tableau d’Arielle

Dans les cases du tableau, Arielle veut placer chacun des chiffres de 1 à 8. Le deuxième nombre doit être le double du premier. Le troisième doit être le triple du premier. Le quatrième doit être le double du deuxième.

Remplissez le tableau pour que la somme des quatre nombres soit 180.

8. Blessure d’Océane

Océane commença l’école un mardi 5 septembre.

Elle se blessa à une cheville le 5 octobre.

Quel jour de la semaine était-ce ?

9. Bâtonnets romains

Grégoire a pris 15 bâtonnets. Il a écrit cette égalité en chiffres romains. Ceci se lit 14 + 6 = 6 : ce qui est faux.

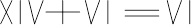
Enlevez quatre bâtonnets de façon que l’égalité soit vraie. Notez que les signes sont formés avec des bâtonnets.

10. Signes de Yoland

Yoland a écrit l’égalité ci-après et a effacé les signes, sauf le signe d’égalité.

Placez un signe (+, –, ´ ou ÷) dans chaque case vide pour que l’égalité soit vraie.

                                                                                                                             Solutions 11 à 20

11. Des pigeons fuyards

Dans un parc, il y a 66 pigeons. Ils se déplacent généralement en un triangle c’est-à-dire qu’il y a un oiseau par devant, deux autres dans la deuxième rangée, trois autres dans la troisième rangée et ainsi de suite. Un jour, dans un déplacement, tous les pigeons du centre du triangle quittent. Il ne reste que ceux de la bordure.

Combien reste-t-il de pigeons ?

12. Agenda d’Ursule

Pour son anniversaire de naissance,

Ursule a reçu de ses parents un agenda de 123 pages.

Combien Ursule devra-t-elle utiliser de chiffres pour paginer son agenda ?

13. Blocs d’Alicia

Dans sa boîte de jouets, Alicia trouve neuf cubes numérotés de 1 à 9. Elle dessine une grille et y place trois blocs : 3, 7 et 8.

Placez les six autres blocs pour que l’addition soit vraie.

14. Cadre d’Ariane

Ariane a préparé un cadre carré en bois de 18 centimètres de côté.

Elle attache une boucle à tous les 3 centimètres à partir d’un coin.

Combien Ariane a-t-elle attaché de boucles ?

15. Impairs d’Alain

Alain écrit les cinq plus petits nombres impairs : 1, 3, 5, 7 et 9.

Il fait leur somme et obtient 25.

Puis, il extrait la racine carrée de 25 qui est 5.

Trouvez la racine carrée de la somme des 20 plus petits nombres impairs.

16. Poulets d’Ovide

Ovide fait l'achat de 42 poulets.

La vendeuse lui recommande de les placer dans quatre enclos adjacents.

Il doit toujours y avoir cinq poulets de plus dans l'enclos de droite.

Combien Ovide distribuera-t-il de poulets dans chaque enclos ?

17. Addition de Germaine

Germaine utilise chacun des chiffres de 2 à 7 pour réaliser une addition de trois nombres de deux chiffres. La somme est un nombre de trois chiffres.

Quelle est la plus grande somme possible ?

18. Monstre à 4 têtes

Le monstre est un nombre de quatre chiffres qui sont ses quatre têtes.

Le monstre a deux têtes qui sont 6 et 7.

Le monstre peut être partagé en 7 parties égales.

La somme des têtes du monstre est 22.

Quel est le plus petit monstre ?

19. Découverte de Mathys

Mathys a découvert une disposition remarquable de nombres.

En vous basant sur ces résultats, trouvez la valeur de 3 333 333 × 3 333 333.

20. Triangle d’Yvon

Yvon dispose les nombres consécutifs à partir de 1 en un triangle comme ceci :

Quel sera l’avant-dernier terme de la neuvième ligne si on continue à écrire les entiers selon la même règle ?

                                                                                                                       Solutions 21 à 30

21. Lectures imagées

Samuel est un lecteur assidu de bandes dessinées.

En mai, il a lu deux albums de moins qu’en avril.

En juin, il a lu le double d’albums qu’en mai.

En juillet, il a lu un album de plus qu’en juin.

Un calcul rapide l’a amené à conclure qu’il avait lu 19 albums pendant ces quatre mois. En fait, il s’est trompé. Il en a lus légèrement plus que 19.

Combien Samuel a-t-il lu d’albums pendant ces quatre mois ?

22. Une bonne marche

Fred-Éric emprunte une piste destinée aux marcheurs et aux coureurs.

La première heure, il parcourt le huitième de la longueur de la piste, plus un kilomètre.

La deuxième heure, il parcourt le quart de la distance qui reste, plus un kilomètre.

La troisième heure, il parcourt la moitié de la distance qui reste, plus un kilomètre.

Il lui reste à parcourir les six derniers kilomètres.

Quelle est la longueur de la piste ?

23. Figures de Marcelle

Marcelle a écrit deux égalités avec quatre figures différentes. Chaque figure représente un chiffre différent. Dans chaque égalité, le résultat est un nombre de deux chiffres.

                                                           & + & = - (

                                                           & + & + & = * -

Quelle est la valeur de & ?

24. Mois de juillet

Samuel prend la feuille d’un calendrier d'un mois de juillet.

Trouvez six nombres disposés en un rectangle dont la somme est 123.

25. Astuce de Mathis

Mathis a écrit des nombres dans le tableau ci-après. Il choisit un seul nombre par ligne et un seul par colonne. Il additionne simultanément ces quatre nombres.

Combien y a-t-il de sommes possibles ?

26. Tableau de Gabriel

Gabriel a préparé le tableau ci-après. En utilisant les nombres 5, 6, 7, 8, 9, 11, 12, 17, 21, 22, 24, il remplit les cases vides de telle manière qu'il y a un nombre dans chaque case.

À la fin, il restera un nombre. Quel est ce nombre ?

27. Une mère et sa fille

Il y a quatre ans, Laurence avait le triple de l’âge d’Olivia.

Dans quatre ans, les deux auront vécu 76 ans.

Quel est l’âge de chacune actuellement ?

28. Samantha efface

Samantha a écrit quatre nombres dont la somme est 1277. Elle a effacé deux de ces nombres. L’un est le double de l’autre.

Quels sont ces deux nombres ?

29. Résultats scolaires

Dans un examen de mathématiques sur 20 points,

Christophe et Laurianne ont eu ensemble 27 points.

Laurianne et Germain ont eu ensemble 34 points.

Christophe et Germain ont eu ensemble 31 points.

Quelle est la note de Germain ?

30. Choix d’un nombre

Je suis un nombre de cinq chiffres différents.

La somme de mon premier et de mon deuxième chiffre est 5.

La somme de mon premier et de mon quatrième chiffre est 12.

La somme de mon deuxième et de mon troisième chiffre est 7.

La somme de mon premier et de mon cinquième chiffre est 7.

Mon troisième est le double de mon cinquième.

Qui suis-je ?

                                                                                                                         Solutions 31 à 40

31. Randonnées en bicyclette

Émilie part pour une randonnée en bicyclette un lundi.

Elle parcourt 7 kilomètres ce jour-là et elle augmente de 3 kilomètres chaque jour qui suit.

Deux jours plus tard, soit le mercredi, Clara part à son tour.

Elle parcourt 13 kilomètres ce jour-là et elle augmente de 2 kilomètres chaque jour qui suit.

Quel jour de la semaine Émilie va-t-elle parcourir 10 kilomètres de plus que Clara ?

32. Seulement des pairs

Tristan a représenté 45 avec quatre 5.

55 – 5 – 5 = 45

Représentez 45 avec quatre chiffres pairs identiques.

33. Cases de Pierre

Pierre a dessiné la figure suivante dans laquelle une case porte le numéro 2.

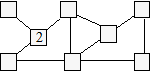
Placez un chiffre par case pour qu’en suivant les traits on puisse lire ces trois nombres : 1234, 2647 et 5973.

34. Visites au cinéma

Cinq amis sont allés au cinéma pendant la dernière année. Ils ont vu en tout 30 films.

Adam a vu trois films de moins que Brandon.

Clara a vu trois films de plus que Diane.

Diane a vu deux films de moins qu’Édouard

Édouard a vu un film de plus qu’Adam.                                  

Combien de films chacun a-t-il vu ?

35. Trois générations

Une mère a le double, moins 2, de l’âge de sa fille.

La grand-mère a le double, plus 2, de l’âge de la mère.

Les trois ont ensemble 129 ans.

Quel est l’âge de la fille ?

36. Monnaie de Méganie

Méganie ouvre sa tirelire qui contient 200 pièces de monnaie.

Elle dispose 18 pièces sur une première rangée, 17 sur une deuxième, 16 sur une troisième

et ainsi de suite en plaçant une pièce de moins par rangée.

Elle termine quand la dernière rangée est formée de 2 pièces.

À la fin, combien restera-t-il de pièces de monnaie dans la boîte ?

37. Jetons de Benjamin

Benjamin découpe sept jetons et les numérote de 2 à 8.

Il prend deux jetons à la fois et additionne les numéros.

Par exemple, le jeton 3 plus le jeton 5 = 8.

Trouvez le nombre de paires de jetons dont la somme est divisible par 3.

38. Cartes de Débora

Débora a un certain nombre de cartes de baseball dont elle veut se départir.

Elle donne la moitié de ses cartes à Charlyne, plus 10 cartes.

Par la suite, elle donne la moitié des cartes restantes, plus 10, à Angélo.

Enfin, elle donne la moitié des cartes restantes, plus 10, à Jean-René.

À ce moment, il ne lui reste plus aucune carte.

 De combien de cartes de baseball Débora voulait-elle se départir ?

39. Médaillons de Sabine

Sabine a placé ses 47 médaillons dans trois boîtes. Si elle retranche un médaillon de la boîte A, elle en contient deux fois plus que la B. Si elle retranche deux médaillons de la boîte B, elle en contient deux fois moins que la C.

Combien y a-t-il de médaillons dans chaque boîte ?

40. Gains de dominos

Lors d’activités ludiques, des enfants reçoivent des dominos comme récompenses.

Clara et Éva ont gagné ensemble 29 dominos.

Éva et Jérémie ont gagné ensemble 26 dominos.

Jérémie et Clara ont gagné ensemble 21 dominos.

Combien de dominos en tout ont gagné ces trois enfants ?

                                                                                                                        Solutions 41 à 50

41. Naissances rapprochées

Andrée et Nicole sont nées dans la même année.

Andrée est née un jeudi 4 mai.

Nicole est née 100 jours plus tard.

En quel jour de la semaine Nicole est-elle née ?

42. Allocations de Victoria

Chaque semaine, Victoria reçoit le même montant d’argent de ses parents.

Elle en dépense la moitié et conserve le reste.

Au bout de sept semaines, elle a accumulé 42 $.

Combien d’argent Victoria reçoit-elle chaque semaine ?

43. Un premier casse-tête

Quand Sofia reçut son premier casse-tête, sa mère demanda à son fils aîné de deviner le nombre de morceaux. Elle lui dit :

« Choisis un nombre. Fais les opérations dans cet ordre : multiplie par 3, additionne 7 et divise par 2. Tu obtiendras 26. Le nombre que tu dois choisir est le nombre de morceaux. »

Combien le casse-tête de Sofia contient-il de morceaux ?

44. Croisés d’Henriette

Henriette a préparé la grille 4 × 4 ci-après dans laquelle elle a noirci quatre cases. On doit placer un chiffre par case pour former des nombres horizontalement et verticalement. Pour ce faire, des indices sont donnés, même pour les chiffres seuls.

A. J’ai un 6 et un 8 - Je suis un nombre impair.

B. J’ai un 2, un 6 et un 7.

C. J’ai un 1, un 3 et un 4.

D. Je suis un carré - J’ai deux chiffres identiques.

E. Je suis divisible par 3 - Je suis un carré impair.

F. J’ai un 2, un 3 et un 8.

G. Je suis divisible par 5.

H. J’ai un 3 et un 7 - Je suis un impair.

Remplissez la grille.

45. Noisettes d’Émilie

Émilie fait des provisions de noisettes, souvent pour les donner.

À chaque semaine, elle fait deux opérations dans cet ordre.

1. Elle achète des noisettes autant qu’elle en a.

2. Elle donne 10 noisettes.

Au bout de quatre semaines, Émilie a 42 noisettes.

Combien Émilie avait-elle de noisettes au début ?

46. Visite au parc

Moins de 40 enfants visitent un parc d’attractions.

Lorsqu’ils occupent des manèges à quatre places, le dernier manège a un siège libre.

Lorsqu’ils occupent des manèges à sept places, le dernier manège a aussi un siège libre.

Combien y a-t-il d’enfants dans ce groupe ?

47. Partage de Clara

Clara a distribué 16 nombres dans une grille. Elle doit maintenant partager cette grille en quatre parties de même forme et de même grandeur. De plus, la somme des nombres contenus dans chaque partie doit être égale à 30.

Faites le partage.

48. Vignettes de Naomie

Naomie fait le ménage de sa chambre.

Elle décide de se départir de ses vignettes.

Elle en donne la moitié, moins 3, à sa jeune sœur.

Elle donne la moitié des vignettes qui restent, plus 3, à son jeune frère.

Elle donne les 10 vignettes qui restent à une amie.

 Combien Naomie possédait-elle de vignettes ?

49. Ballons de Manuel

Comme responsable des articles de sport dans un gymnase,

Manuel a la tâche d’entreposer 100 ballons.

Il doit placer trois ballons dans un premier casier

et cinq ballons dans chacun des autres casiers jusqu’à épuisement du stock.

Combien y aura-t-il de ballons dans le dernier casier ?

50. Œufs de Léopold

En bon père, Léopold veut gâter ses enfants en leur achetant des œufs de Pâques.

S’il donnait deux œufs à chacun d’eux, il lui en resterait trois.

S’il donnait trois œufs à chacun d’eux, il lui en manquerait quatre.

Combien Léopold a-t-il d’enfants ?

                                                                                                                                Solutions 51 à 60

51. Pommes de Rose

Rose a acheté un panier qui contient 87 pommes.

Elle veut en partager le contenu avec son frère et sa sœur.

Son frère doit avoir 25 pommes de plus que sa sœur.

Pour sa part, elle se contenterait du tiers des pommes de son frère.

Combien chacun aura-t-il de pommes ?

52. Distribution de Valérie

Valérie veut placer les chiffres 2, 5, 6, 7, 8 et 9 dans les six cases de façon que la somme soit bonne. Le premier nombre est inférieur de 41 au deuxième.

Distribuez les six chiffres.

53. Horloge de Thomas

Thomas a trouvé le cadran d’une horloge dans un grenier. Il a remplacé les nombres par ceux-ci.

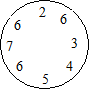
Partagez le cadran en trois parties pour que la somme des nombres de chaque partie soit trois nombres consécutifs.

54. Initiales de Pascal

Pascal a écrit l’égalité ci-après dans laquelle chaque lettre est l’initiale d’un nombre.

QVT + DN = CD

Quelle est la plus grande valeur de CD ?

55. Envolées de Bernard

Bernard dessine des visages et des avions. Il produit trois rangées d’icônes selon une certaine régularité d'une rangée à l'autre.

J Q Q Q

J J J Q Q Q Q Q Q

J J J J J J J Q Q Q Q Q Q Q Q Q

Combien y aura-t-il d’icônes dans la huitième rangée ?

56. Randonnées de Tristan

Le 15 d’un mois, Tristan a fait une randonnée au parc des Cèdres.

Le 13 du mois suivant qui était le même jour de la semaine,

il a fait une randonnée au parc des Épinettes.

Dans une année donnée, combien de fois le 15 d’un mois et le 13 du mois suivant peuvent-ils être le même jour de la semaine ?

57. Tableau d’Agathe

Agathe a écrit les nombres dans le tableau ci-après selon une certaine règle. Elle continue d’écrire les nombres sans dépasser 52, toujours en suivant la même règle.

Combien de nombres de 2 à 52 sont ou seront absents du tableau ?

58. Relations de Malorie

Malorie joue avec les relations qui existent entre les nombres. Elle veut placer dans cette grille les nombres : 8, 9, 10, 13, 14, 15, 16, 19, 20, 22 et 24. Toutefois, un nombre est exclu.

Quel est ce nombre ?

59. Tablettes de Thomas

Thomas a inscrit dans le tableau ci-après le nombre de tablettes vendues pendant les quatre premiers jours de deux semaines. Il y a erreur dans le tableau. En réalité, 36 tablettes ont été vendues la première semaine et 34 la deuxième semaine.

Intervertissez deux nombres inscrits d’une semaine à l’autre de façon à corriger l’erreur.

60. Meilleure route

Jean-Pierre part du point A pour se rendre au point B. Des postes de péage à tarifs différents sont placés sur son parcours.

l : 10 florins               n : 25 florins              u : 40 florins

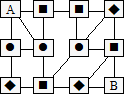
Trouvez la route la moins coûteuse.

                                                                                                                            Solutions 61 à 70

61. Feuille volante

Valentine a déchiré une feuille de calendrier de l'an 2013. Sa mère a trouvé cette pièce qui apparaît ci-après. Elle sait que le 1^er janvier 2013 était un mardi.

Quel mois correspond à cette pièce de calendrier ?

62. Dominos de Chloé

Chloé a placé cinq dominos comme il est illustré ci-après. Elle a noté que la rangée supérieure contient 7 points et que la rangée inférieure en contient 17. Elle demande à son ami de renverser trois dominos afin d'obtenir le même nombre de points dans chaque rangée horizontale.

Quels seront les dominos qui seront renversés ?

63. À livre ouvert

Bella a ouvert un livre de mathématiques aux pages 62 et 63.

La somme des numéros des pages est 125.

Un autre jour, Bella a ouvert le même livre aux pages telles que :

1. La somme des numéros est un nombre de deux chiffres identiques.

2. Aucun chiffre n’est un 5 ou un 7.

Quel est le numéro de la page de gauche à ce moment ?

64. Amélia et ses amis

Amélia écrit huit prénoms sur des cartons de même format. Elle les place dans un panier. Elle tire un nom du panier et le replace aussitôt.

Après avoir fait 16 tirages, selon toute probabilité, combien de fois Amélia tirera-t-elle son prénom ?

65. Choix de Tristan

Tristan choisit deux nombres.

Il soustrait ces deux nombres l’un de l’autre. La différence est A.

Il additionne 12 au plus grand nombre.

Il soustrait 5 au plus petit.

Il soustrait ces deux derniers résultats. La différence est B.

À quoi est égal B - A ?

66. Balances de Christine

Christine utilise deux balances à plateaux pour connaître la masse de deux modèles de briques qu'elle veut acheter. Elle fait deux pesées, comme il est illustré. Les briques marquées d’une même lettre ont la même masse.

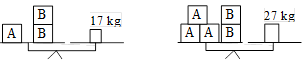
Quelle est la masse des briques des deux modèles ?

67. Fête d’autruches

Un certain nombre de couples d’autruches participent à une fête.

Chaque autruche donne une de ses plumes à chacune des autres, sauf à son ou à sa partenaire.

À la fin, 40 plumes données sont mises dans une première boîte et les 80 autres dans une seconde boîte.

Combien y a-t-il de couples d’autruches à la fête ?

68. Valse de Grégoire

Grégoire a écrit les nombres de 1 à 16 comme ci-après. Le 15 apparaît en haut de la quatrième colonne pleine. Grégoire désire continuer à écrire les nombres tout en respectant le même modèle.

Quel nombre se trouvera en haut de la 10^e colonne pleine ?

69. Âge d’Anthime

Grand-père Anthime dit à son petit-fils : « Il y a 28 ans, j’avais l’âge actuel de ton père.

Dans 28 ans, tu auras l’âge de ton père.

Il y a deux ans, ton père et moi, nous avions 94 ans ensemble. »

Quel est l’âge actuel de chacun ?

70. Cases de Patricia

Patricia a dessiné six cases de façon à recevoir trois nombres de deux chiffres.

La somme des nombres doit être la plus grande possible.

Le troisième nombre est inférieur de 13 au deuxième.

Les chiffres utilisés sont 1, 2, 3, 4, 5 et 6.

Quelle est la plus grande somme ?

                                                                                                                                Solutions 71 à 80

71. Tirage de Caroline

Caroline place quatre jetons dans une boîte : deux verts et deux jaunes.

Elle tire deux jetons à la fois et les replace dans la boîte.

Quelle est la probabilité d’obtenir deux jetons verts ?

72. Allumettes de Romain

Avec des allumettes, Romain a écrit : 6 + 2 = 5 en chiffres romains. Cette égalité est fausse.

Déplacez une allumette pour avoir une égalité vraie.

73. Période de cadeaux

Lors de la fête de Noël, les enfants d’une famille se donnent mutuellement des cadeaux.

Les parents donnent un seul cadeau à chacun des enfants et n’en reçoivent pas de leurs enfants. Une boucle rouge apparaît sur chaque cadeau.

La mère a compté 49 boucles.

Combien y a-t-il d’enfants dans cette famille ?

74. Offres louables

Céline met une statuette en vente pour un montant de 100 ducats.

Un premier client arrive et dit : « Je vous offre un tiers et une demie de ce que vous demandez. »

Un autre dit : « Je suis prêt à vous donner les 4/5 de ce que vous demandez. »

Quelle offre est la plus avantageuse ?

75. Grand-maman vieillit

Nous sommes un dimanche de janvier en 2010.

C’est la fête de grand-maman.

Elle a 75 ans aujourd’hui.

Quel âge aura grand-maman quand on fêtera à nouveau son anniversaire un dimanche ?

76. Passe-temps de Maéva

Quand Maéva s’ennuie, pour passer le temps,

elle regarde le cadran à affichage numérique de son enregistreur.

Elle essaie de deviner à quel moment précis le chiffre des minutes changera.

Combien de fois le 2 apparaîtra-t-il entre 1 heure et 2 heures ?

77. Cartes de Martin

Martin découpe cinq cartes. Sur chacune, il écrit un 4.

4       4       4       4       4

À l’aide d’opérations, représentez 32 en utilisant cinq 4.

78. Livres de Roméo

Roméo s’est fait construire une bibliothèque comportant quatre tablettes.

Sur la tablette du bas, il place un tiers de ses livres, plus 3.

Sur la deuxième tablette en partant du bas, il place un quart de ses livres, plus 4.

Sur la troisième tablette, il place un sixième de ses livres, plus 5.

Comme tous les livres sont placés, la tablette du haut est ornée de bibelots.

Combien Roméo possède-t-il de livres ?

79. Œufs à vendre

Trois voisins ont chacun un petit poulailler.

Le propriétaire de l’ouest a cinq poules de moins que celui du centre.

Celui du centre a 11 poules de plus que celui de l’est.

Celui de l’ouest a six poules de plus que celui de l’est.

Ils ont en tout 68 poules.

Combien de poules contient chaque poulailler ?

80. Poêle antique

Lors des journées humides d’automne, au chalet, Béatrice utilise chaque jour la même quantité de rondins pour chauffer son poêle à bois.

En novembre de l’année dernière, pendant la première moitié du mois, un tiers, moins 3, des journées furent humides.

Pendant la deuxième moitié, un cinquième, plus 5, furent humides.

Béatrice a utilisé, pendant ce mois, 240 rondins.

Combien de rondins en moyenne Béatrice a-t-elle utilisé chaque jour de temps humide ?

                                                                                                                           Solutions 81 à 90

81. Tante Amélie

Léanne a 8 ans. Sa sœur Léonie a 11 ans.

Leur différence d’âge est de 3 ans.

Dans 5 ans, la somme de leur âge sera de 29 ans,

tout comme l’âge de leur tante Amélie.

Quelle sera la différence d’âge de Léanne et de Léonie dans 5 ans ?

82. Mots croisés

Une grille de mots croisés 12 × 12 contient deux cases noires par ligne et deux cases noires par colonne. Victoria a déjà écrit une lettre dans 12 cases.

Combien de cases reste-t-il à remplir ?

83. Des parascolaires

Dans une classe, tous les élèves sont inscrits à au moins une activité parascolaire : 19 élèves au bricolage, 20 à la broderie, 7 à la fois au bricolage et à la broderie.

Combien y a-t-il d’élèves dans cette classe ?

84. L’âne de sa mère

Petit Paul que sa mère appelle mon âne préféré a fait l’addition ci-après. Il a trouvé 137 alors que la somme est 139.

48 + 51 + 40 = 137

Remplacez deux chiffres par 3 pour obtenir une somme de 137.

85. Opérations de Victor

Victor dit à sa sœur : « Je prends 80 et en faisant les opérations suivantes, j’obtiens 66 à la fin. »

En partant de 80, faites les mêmes opérations mais dans un autre ordre et obtenez ainsi 102.

86. Croix d’Élodie

Dans cette grille, Élodie a écrit des nombres de 2 à 18. Dans la croix qui apparaît, la somme des nombres est 50.

Trouvez une croix dont la somme des nombres est 47.

87. Insomnies communes

Le 30 juin au matin, Éloi et Éloïse se confient qu’ils ont mutuellement fait des insomnies pendant la nuit. Par la suite, Éloi fait des insomnies à toutes les trois nuits et Éloïse à toutes les quatre nuits.

Combien de fois les deux amis feront-ils d’insomnies la même nuit du 1^er juillet au 31 août ?

88. Monnaie de Lise

Lise a six pièces de monnaie comprenant au moins une pièce parmi les 5 ¢, les 10 ¢ et les 25 ¢. Son montant est de 60 ¢.

Quelles sont ces pièces ?

89. Jetons de Nadia

Nadia a découpé cinq jetons et les a tous numérotés 6.

Placez un signe +, –, × ou ÷ entre les jetons de façon que le résultat soit 31.

90. William domine

William a réparti 49 dominos dans 7 sacs.

Chaque sac contient un nombre différent de dominos.

De plus, les nombres sont consécutifs.

Combien y a-t-il de dominos dans le sac qui en contient le plus ?

                                                                                                                            Solutions 91 à 100

91. Raccourcis de Majorie

Majorie écrit les nombres par l’initiale de chaque mot qui le compose. Ainsi, 326 s’écrit TCVS, tout comme 327 d’ailleurs. Majorie a fait cette addition.

C C C + S C D S + N C Q V Q = D M D C S U

Quelle est la somme ?

92. Jetons de Manon

Manon a découpé cinq jetons et les a numérotés comme ci-après.

Placez des signes +, –, ´ ou ÷ entre les chiffres sans changer l’ordre des jetons. Le résultat doit être 15.

93. Bon thé

Télesphore a écrit les nombres de 1 à 40 dans la grille. Il colorie un T de taille réduite comme ci-après. La somme des nombres des quatre cases de ce T est 20.

Trouvez quatre nombres qui sont disposés en T, comme dans l’exemple, et dont la somme est 128.

94. Addition de Christian

Christian a choisi trois nombres de deux chiffres dont la somme est 136.

Le premier nombre est 43.

L’un des deux autres nombres est le double de l’autre.

Trouvez les deux nombres qui manquent.

95. Boîte de Balthazar

Dans sa boîte aux lettres, Balthazar prend six lettres différentes et forme un mot. Il donne des indices à son ami pour qu’il découvre le mot.

1. La valeur de chaque lettre est son rang dans l’ordre alphabétique.

2. La somme des rangs des deux premières lettres est 31.

3. La somme des rangs des deux lettres du milieu est 41.

4. La somme des rangs des deux dernières lettres est 23.

5. Dans les deux premiers couples, deux lettres sont voisines en ordre alphabétique peu importe l’ordre.

6. Ce mot contient trois consonnes.

Quel est ce mot ?

96. Cent de Mathis

Mathis a représenté 100 avec cinq 3. Voici ce qu’il a écrit :

33 × 3 + 3/3 = 100

À l’aide d’opérations simples, représentez 100 avec quatre 5.

97. Calendrier d’Aimée

Aimée a inventé un nouveau calendrier.

Il est formé de 12 mois de 30 jours chacun.

Le 11 octobre est un mardi.

Quel sera le jour de la semaine du 11 décembre ?

98. Cumul de Micheline

Micheline compose tous les nombres possibles de trois chiffres

 avec les chiffres 1, 2 et 3.

Elle désire trouver la somme de ces nombres

sans additionner plus de deux nombres à la fois.

Quelle est la somme de ces nombres ?

99. Partage de noix

Mariette a six enfants.

Chaque fois qu’elle va au marché, elle achète des noix.

En arrivant à la maison, elle répartit également les noix entre ses enfants et conserve le reste.

Après être allée au marché cinq fois, elle a conservé un nombre différent de noix.

Combien Mariette a-t-elle conservé de noix ?

100. Sommeil léger

Jérémie ne réussissait pas à s’endormir.

Il se mit à compter les moutons en fuite.

Quand ils sautaient la clôture 3 par 3, il en restait 2.

Quand ils sautaient 4 par 4, il en restait encore 2.

Quand ils sautaient 5 par 5, il en restait encore 2.

Combien y avait-il de moutons au minimum dans ce troupeau ?

                                                                                                                       Solutions 101 à 110

101. Signes de François

François a préparé le tableau ci-dessous dans lequel il a écrit deux nombres et six signes.

Complétez les trois égalités avec chacun des nombres de 1 à 7.

102. Yakov opère

À l’aide d’opérations simples, on peut représenter beaucoup de nombres en utilisant quatre chiffres 4. Yakov a trouvé ces trois égalités lorsque le résultat est successivement 7, 8 et 9.

44/4 – 4 = 7

4 × 4 – 4 – 4 = 8

4 + 4 + 4/4 = 9

Trouvez une égalité pour chacun de ces trois résultats : 15, 16 et 17.

103. Cible d’Hélène

Hélène fabrique une cible formée de trois zones.

Les points possibles par zone sont 3, 7 et 12.

Son ami a lancé neuf flèches dans la cible pour un total de 57 points.

Il a atteint la zone 3 une fois de plus que la 7.

Combien de fois l’ami a-t-il atteint chaque zone ?

104. Rimouski-Québec

Sacha part de Rimouski à midi et se dirige vers Québec.

Son automobile roule à une vitesse moyenne de 90 kilomètres à l'heure.

Au même moment, Jim part de Québec et se dirige vers Rimouski.

Son automobile roule à une vitesse moyenne de 100 kilomètres à l'heure.

La distance entre les deux villes est de 310 kilomètres.

Quelle sera la distance entre les deux automobiles deux heures après le départ ?

105. Grille d’Élisa

Élisa a préparé la grille ci-après. En se servant des indices donnés, on peut placer un chiffre par case de façon à former des nombres horizontalement et verticalement comme dans les mots croisés.

Remplissez la grille.

106. Timbré et Délurée

Timbré a acheté cinq enveloppes de timbres. Sur chaque enveloppe, il a écrit le nombre de timbres. Toutefois, il a interverti les nombres de deux enveloppes. Par exemple, il aurait dû écrire 15 sur la première enveloppe et 23 sur la deuxième.

23    15    18    20    36

De son côté, Délurée a aussi cinq enveloppes dont chacune possède 10 timbres de plus que chaque enveloppe de Timbré.

Combien Délurée possède-t-elle de timbres ?

107. Jetons de Stella

Stella découpe cinq jetons. Sur chacun, elle écrit un 5.

5       5       5       5       5

À l’aide d’opérations simples, représentez 25 en utilisant cinq 5.

108. Premiers pas

Gabriel est né  le 2 janvier 1999.

C’était un beau samedi d’hiver.

Le 1^er janvier 2000, il fit ses premiers pas.

Quel jour de la semaine Gabriel fit-il ses premiers pas ?

109. Carottes de Lydia

Pour le souper en famille, Lydia arrache des carottes dans trois carreaux : P, Q et R.

Le carreau P lui fournit 2 carottes de plus que le Q.

Le carreau Q lui fournit 2 carottes de plus que le R.

Le carreau R lui fournit la moitié des carottes de P.

Combien Lydia a-t-elle récolté de carottes en tout ?

110. Virginie opère

Virginie a préparé le tableau ci-dessous dans lequel elle a écrit deux nombres et six signes.

Complétez le tableau pour qu’à la fin chacun des nombres de 1 à 9 y apparaisse.

                                                                                                                           Solutions 111 à 120

111. Paie de Jérémie

Jérémie vient de recevoir sa première paie. Il écrit sur sa calculatrice 3 771 350. Il la tend à son amie Louise et lui dit :

- Voici ce que je viens de gagner.

- Je ne crois pas, de reprendre celle-ci, que tu aies gagné autant.

Que doit faire Louise pour savoir ce que Jérémie a gagné ?

112. Une mère devineresse

Estelle a un dé dans chaque main. Sa mère lui dit :

« Je peux deviner la marque de chaque dé. Voilà ce que tu vas faire : Double la marque du dé de la main gauche. Additionne 3. Multiplie le résultat par 5. Soustrais 3. Additionne la marque du dé de la main droite. Donne-moi le résultat. »

Quelle opération devra faire la mère d’Estelle pour deviner les deux marques ?

113. Souvenir d’une année

À la fin du 20^e siècle, l’agencement des chiffres de l’année pour représenter certains nombres était très populaire. Au début du 21^e siècle, cet engouement s’est estompé principalement à cause de la présence de deux zéros dans le millésime.

Sauriez-vous représenter 2013 en utilisant deux fois chacun de ses chiffres ?

114. Calendrier de Samuel

Samuel prend une feuille de calendrier d’un mois de décembre. Il délimite des carrés 2 × 2 qui contiennent quatre nombres.

La somme des nombres de chaque carré 2 × 2 est toujours divisible par 4. Pourquoi ?

115. Tour de magie

Martin remet à ses élèves la correction d’un examen de mathématiques sur 100 points dont la plus basse note est 40. Tout de suite après, il propose à ses élèves le tour suivant : « Prenez une calculatrice. Inscrivez 273. Multipliez ce nombre par votre note. Multipliez le résultat par 37. »

Tous les élèves s’exclament. Ils ont aperçu leur note en triple à l’écran. Pourtant, il y a un élève qui ne comprend pas la réaction des autres.

Expliquez cela.

116. Surprises du calendrier

En 2011, deux mois avaient exactement la même page de calendrier c’est-à-dire que le premier jour du mois était le même jour de la semaine et que le nombre de jours était identique. Voici la page du calendrier de janvier 2011 :

En 2011, trouvez l’autre mois qui avait exactement la même page de calendrier.

117. Magie de Martin

Martin dit à Martine : - Choisis deux nombres inférieurs à 10. Additionnes-les ; puis additionne successivement le dernier nombre à leur somme. Par exemple, tu pourrais avoir : 4, 5, 9, 14, 23, 37, etc. Quand tu auras trouvé les sept premiers nombres, tu me les montres pendant deux secondes ; puis tu continues jusqu’au 10^e nombre. Additionne alors les 10 nombres. Pendant que tu fais ces opérations, je vais essayer de trouver cette somme.

Comment s’y prendra Martin pour trouver la somme ?

118. Fouille de cerveaux

Le fou du roi a compté respectivement

505

5050

50 505

grains de poussière dans le cerveau de trois sujets. Il dit au roi :

« Sans faire le total des grains, je pourrais inoculer tous ces grains de poussière à quatre autres de vos sujets et il ne resterait aucun grain. »

Expliquez au roi comment le fou s’y est pris pour arriver à cette conclusion.

119. Astuce de Fabienne

Fabienne a amassé des noisettes. Elle dit à Fabien :

- J’ai ici 18 noisettes. Place ces noisettes dans trois boîtes de telle sorte que chaque boîte contienne un nombre impair de noisettes.

- C’est impossible, de répondre Fabien. Comme 18 est pair, il pourra être partagé au plus en deux impairs.

- Il y a pourtant une façon de réussir ce partage.

Partagez les 18 noisettes dans trois boîtes de façon que chaque boîte contienne un nombre impair de noisettes.

120. Un euro égaré

Julie reçoit 20 euros. Elle dépense successivement 5, 9 et 6 euros. Elle fait ses comptes et additionne les montants des deux colonnes.

Comment expliquer la différence d’un euro entre les deux colonnes ?

 Suite des passe-temps arithmétiques