Solution 1. On peut distribuer les jetons ainsi : 13 + 28 + 46 + 57 = 144.

Solution 2. Trefflé a dessiné 171 trèfles.

Solution 3. Jeannette est revenue le 8 juillet.

Solution 4. On peut représenter 72 ainsi : (3³ – 3) × 3.

Solution 5. Luce devra dessiner 36 bicyclettes.

Solution 6. Voici une façon de remplir le tableau :

Solution 7. Les quatre nombres sont 18, 36, 54 et 72.

Solution 8. C’était un jeudi.

Solution 9. On enlève les deux bâtonnets formant le V de 14. On enlève le bâtonnet vertical du +. On enlève le dernier bâtonnet du 6 du deuxième membre de l’égalité. Ceci se lit : XI – VI = V.

Solution 10. Une égalité est : 5 × 4 + 7 = 9 × 6 ÷ 2.

Solution 11. Il reste 30 pigeons.

Solution 12. Ursule devra utiliser 261 chiffres.

Solution 13. L’addition est : 359 + 127 = 486.

Solution 14. Ariane a attaché 24 boucles.

Solution 15. La racine carrée de la somme des 20 plus petits nombres impairs est 20. La racine carrée de la somme de termes impairs consécutifs à partir de 1 correspond toujours au nombre de termes.

Solution 16. La distribution se fait ainsi : 3, 8, 13, 18 poulets.

Solution 17. La plus grande somme est 189. On pourrait avoir : 53 + 64 + 72 = 189.

Solution 18. Le plus petit monstre est 1687.

Solution 19. Le résultat est 11 111 108 888 889.

Solution 20. L’avant-dernier terme sera 44.

Solution 21. Samuel a lu 21 albums : 5 en avril, 3 en mai, 6 en juin, 7 en juillet.

Solution 22. La piste mesure 24 kilomètres.

Solution 23. La valeur de & est 7.

Solution 24. Les nombres sont : 13, 14, 20, 21, 27, 28.

Solution 25. Il y a une seule somme possible : c’est 34.

Solution 26. Le nombre qui reste est 9. Le tableau rempli est :

Solution 27. Laurence a 49 ans et Olivia a 19 ans.

Solution 28. Les deux nombres sont 143 et 286.

Solution 29. Germain a eu 19 points pendant que Christophe a eu 12 points et Laurianne 15 points.

Solution 30. Le nombre est 41 683.

Solution 31. Le samedi de la semaine suivante. Ce jour-là, Émilie aura parcouru 43 kilomètres et Clara 33 kilomètres.

Solution 32. On peut écrire 44 4/4.

Solution 33. Voici une façon de distribuer les chiffres :

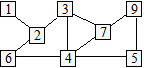
Solution 34. Adam a vu 5 films, Brandon 8, Clara 7, Diane 4 et Édouard 6.

Solution 35. La fille a 19 ans.

Solution 36. Méganie a disposé 170 pièces. Il restera 30 pièces de monnaie dans la boîte.

Solution 37. Il y a sept paires de jetons : (2, 4), (2, 7), (3, 6), (4, 5), (4, 8), (5, 7), (7, 8).

Solution 38. Débora voulait se départir de 140 cartes.

Solution 39. La boîte A contient 21 médaillons, la B 10 médaillons et la C 16 médaillons.

Solution 40. Les trois enfants ont gagné 38 dominos. Clara a gagné 12 dominos, Éva 17 dominos et Jérémie 9 dominos.

Solution 41. Nicole est née un samedi.

Solution 42. Victoria reçoit 12 $ par semaine.

Solution 43. Le casse-tête contenait 15 morceaux.

Solution 44. La grille remplie est :

Solution 45. Émile avait 12 noisettes.

Solution 46. Il y a 27 enfants dans ce groupe.

Solution 47. On partage la grille ainsi :

Solution 48. Naomie possédait 46 vignettes.

Solution 49. Il y aura deux ballons dans le dernier casier.

Solution 50. Léopold a 7 enfants. Il donne 17 œufs.

Solution 51. Rose aura 16 pommes, le frère 48 pommes et la sœur 23 pommes.

Solution 52. La distribution est : 27 + 68 = 95.

Solution 53. La somme des nombres est 39. La somme de chaque partie doit être 12, 13 et 14. Voici une façon de partager le cadran :

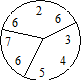
Solution 54. L’égalité est : 93 + 19 = 112. La valeur de CD est 112.

Solution 55. Sur la première rangée, on compte 4 icônes, sur la deuxième 9 icônes, sur la troisième 16 icônes. Dans chaque cas, c’est un carré. En tout, il y aura 81 icônes dans la huitième rangée.

Solution 56. Du 15 d’un mois au 13 du mois suivant, il faut compter 28 jours pour que les deux soient le même jour de la semaine. Cela arrive quand le premier mois a 30 jours. Quatre mois ont 30 jours : avril, juin, septembre et novembre. Cela est possible quatre fois dans une année.

Solution 57. Vingt-quatre nombres de 2 à 52 sont ou seront absents du tableau.

Solution 58. Le nombre qui reste est 19. Le tableau rempli est :

Solution 59. On intervertit les nombres inscrits le jeudi.

Solution 60. La route est formée successivement de l, n, l, n. Elle coûte 70 florins.

Solution 61. Le mois de juin.

Solution 62. Chloé renverse les dominos de rangs 1, 3 et 4.

Solution 63. La page de gauche est numérotée 38.

Solution 64. Sur 16 tirages, Amélia devrait tirer son prénom quatre fois.

Solution 65. La différence est 17.

Solution 66. Chaque brique A a une masse de 5 kilogrammes et chaque brique B a une masse de 6 kilogrammes.

Solution 67. Il y a 6 couples d’autruches à la fête.

Solution 68. Le nombre qui se trouve en haut de la 10^e colonne pleine est 39.

Solution 69. Le petit-fils a 7 ans, son père 35 ans et le grand-père 63 ans.

Solution 70. Dans l’ordre, les nombres sont 32, 64 et 51. La plus grande somme est 147.

Solution 71. On appelle V1 et V2 les deux jetons verts, J1 et J2 les deux jaunes. On peut agencer les jetons ainsi : (V1, V2), (V1, J1), (V1, J2), (V2, J1), (V2, J2) et (J1 et J2). Il y a six façons d’agencer les deux jetons. La probabilité est de 1/6.

Solution 72. On prend l’allumette verticale du signe + et on la place devant le 5 de droite. On a alors :

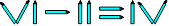
Solution 73. Il y a 7 enfants dans cette famille.

Solution 74. La première offre. Elle représente 5/6 du montant demandé, soit un peu plus de 83 % alors que l’autre offre est de 80 %.

Solution 75. Cela arrivera en 2016. Grand-maman aura 81 ans.

Solution 76. Le 2 apparaîtra 16 fois.

Solution 77. Une expression est : 44 – (4 × 4) + 4.

Solution 78. Roméo possède 48 livres.

Solution 79. Le poulailler de l’ouest contient 23 poules, celui du centre 28 poules et celui de l’est 17 poules.

Solution 80. Béatrice a utilisé 24 rondins par jour.

Solution 81. La différence d’âge ne change pas. Dans 5 ans, elle sera encore de 3 ans.

Solution 82. Il y 24 cases noires. Il reste 108 cases à remplir.

Solution 83. On y compte 32 élèves.

Solution 84. Il convient de remplacer 8 par 3 et 0 par 3. On a donc : 43 + 51 + 43 = 137.

Solution 85. Voici l’ordre des opérations :

Solution 86. La croix est composée de 5, 17, 6, 12 et 7 dans les dernières lignes.

Solution 87. Cinq fois.

Solution 88. Les pièces de Lise sont un 25 ¢, deux 10 ¢ et trois 5 ¢.

Solution 89. Une égalité est : 6 × 6 – 6 + (6 ÷ 6) = 31.

Solution 90. Le sac contient 10 dominos.

Solution 91. CCC se lit 505 ou 550. SCDS se lit 617 ou 717. NCQVQ se lit 984, 994 ou 995. DMDCSU se lit 2261 ou 10 261. L’égalité est : 550 + 717 + 994 = 2261. La somme est 2261.

Solution 92. On fait : 7 ´ 3 – 5 ¸ 2 + 7 = 15. On calcule en suivant l’ordre des opérations.

Solution 93. Les nombres sont 29, 30, 31 et 38.

Solution 94. Les deux nombres qui manquent sont 31 et 62.

Solution 95. Les deux premières lettres sont O et P : 15 + 16 = 31. Les deux lettres du milieu sont T et U : 20 + 21 = 41. Le mot contient trois voyelles. Pour 23, on peut avoir : AV, BU, ER ou IN. Le mot est POUTRE.

Solution 96. On peut représenter 100 ainsi : (5 × 5 – 5) × 5 = 100.

Solution 97. Le 11 novembre est un jeudi. Le 11 décembre sera un samedi.

Solution 98. On fait : 123 + 321 = 444, 132 + 312 = 444, 213 + 231 = 444 et 444 × 3 = 1332. La somme est 1332.

Solution 99. Le nombre de noix achetés n’importe pas. Il reste à Mariette 1, 2, 3, 4 et 5 noix. Mariette a conservé 15 noix en tout.

Solution 100. Il y avait 62 moutons.

Solution 101. Une façon de disposer les nombres est :

Solution 102. Voici une égalité dans chaque cas : 4 × 4 – 4/4 = 15, 4 × 4 – 4 + 4 = 16, 4 × 4 + 4/4 = 17.

Solution 103. L’ami a atteint la zone 3 quatre fois, la 7 trois fois et la 12 deux fois.

Solution 104. La distance est de 70 kilomètres entre les deux automobiles.

Solution 105. La grille remplie est :

Solution 106. Timbré possède 112 timbres. Délurée possède 50 timbres de plus que Timbré. Délurée a 162 timbres. Cela n’a pas d’importance si les nombres de deux enveloppes ont été intervertis.

Solution 107. Une expression est : 55 – (5 × 5) – 5.

Solution 108. Gabriel fit ses premiers pas un samedi.

Solution 109. Lydia a récolté 18 carottes. Le carreau P lui a fourni 8 carottes, le Q, 6 carottes et le R, 4 carottes.

Solution 110. Les égalités peuvent être : 9 – 5 = 4, 6 ÷ 3 = 2 et 1 + 7 = 8.

Solution 111. Louise tourne la calculatrice de 180 degrés. Elle peut lire OSEILLE. Jérémie a gagné de l’oseille : ce qui correspond à fric ou argent en langage populaire.

Solution 112. La mère d’Estelle devra soustraire 12 au résultat donné par sa fille. Le chiffre des dizaines est la marque du dé de la main gauche et l’autre est celle de la main droite.

Solution 113. On peut écrire : (20 + 13) × (20 × 3 + 1) = 2013.

Solution 114. Chaque petit carré contient deux nombres impairs et deux nombres pairs. Or, la somme de deux impairs est paire. De même, la somme de deux pairs est paire. La somme de deux nombres pairs est divisible par 4.

Solution 115. Cela est vrai dans tous les cas où on multiplie par un nombre de deux chiffres. L’élève qui ne comprend pas a eu 100 sur 100. Pourtant, avec une note pareille, il aurait dû ... comprendre.

Solution 116. C’est octobre.

Solution 117. Martin notera le septième nombre. Il multipliera ce nombre par 11.

Solution 118. Les deux derniers chiffres de chacun des trois nombres, soit 05, 50 et 05 ont une somme de 60. Or, 60 est divisible par 4. Quand les deux derniers chiffres d’un nombre sont divisibles par 4, ce nombre l’est aussi.

Solution 119. L’astuce consiste à placer une boîte dans une autre. Par exemple, on peut répartir les noisettes en boîtes de 5, 6 et 7. Quand cela est fait, on place la boîte de 5 noisettes dans celle qui a 6 noisettes. On a une boîte de 5 noisettes, une boîte de 11 et une troisième de 7.

Solution 120. Quand on dépense la moitié du montant qu’on a, il reste le même montant que celui de la dépense. Par exemple, si on a 12 euros et qu’on en dépense 6, il en reste 6. Dans les autres cas, les deux montants sont différents. Aussi, additionner ce qui reste n’a pas de sens.