Solutions 121 à 130

121. Découpage de Normand

Normand découpe six jetons et y inscrit les numéros 2, 3, 4, 5, 6 et 8.

Placez les jetons sur les cases vides de façon à réaliser les deux additions.

122. Différence de Gaétane

Gaétane écrit trois chiffres 0, trois chiffres 3 et trois chiffres 5.

Elle compose deux nombres.

L’un est le plus grand nombre formé

avec au moins un de ces chiffres et au plus deux chiffres identiques.

L’autre est le plus petit nombre formé selon la même règle.

Quelle est la différence entre les deux nombres ?

123. Signes de Mélanie

Mélanie fait l’addition ci-après. La somme des nombres est 100.

3 + 5 + 7 + 14 + 15 + 16 + 18 + 22 = 100

Remplacez deux signes + par deux signes – de façon que le résultat soit 60.

124. Comparaison de gains

Célestine travaille dans un dépanneur au taux horaire de sept florins.

De son côté, Donatien gagne neuf florins l'heure dans une boutique de vêtements.

En comparant leur gain, Donatien se rend compte

qu'il a travaillé cinq heures de moins que Célestine

et qu'il a gagné 15 florins de plus qu'elle.

Quel est le gain total de chacun ?

125. Oranges de Martin

Martin a acheté des oranges.

La quantité d’oranges est égale à la différence entre deux nombres.

Ces deux nombres sont tels que le plus grand diminué de 35

est égal au petit augmenté de 25.

Combien Martin a-t-il acheté d’oranges ?

126. Jetons de Pascal

Pascal a pris quatre jetons numérotés 2, 4, 6 et 8. Il veut les placer sur les cercles de façon que l’égalité soit vraie.

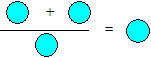
Disposez les quatre jetons.

127. Cordes d’Éric

Éric dessine 15 boules et les relie par des cordes comme ci-après. Il a ainsi formé 16 petits triangles. Il dit à Hélène :

« Dessine six boules et forme une rangée sous le triangle. Aie soin de faire les traits nécessaires. »

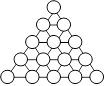
Combien la nouvelle figure contiendra-t-elle de petits triangles ?

128. Gilets d’amies

Mélanie a décidé de numéroter les gilets de ses amies.

Chaque numéro doit être un nombre impair de trois chiffres

qui contient au moins un 7, un 8 ou un 9.

Aucun autre chiffre ne doit être utilisé.

Combien Mélanie peut-elle numéroter de gilets ?

129. Mêmes marques

Horace a découpé cinq jetons et les a tous marqués 8.

Placez un signe +, –, × ou ÷ entre les jetons pour que le résultat soit 66.

130. Cible de Lomer

Lomer lance trois dards sur ce tableau et atteint trois secteurs différents, sauf ceux des cases colorées. Il a gagné ainsi 40 points.

Quels sont les numéros des trois secteurs ?

                                                                                                                   Solutions 131 à 140

131. Carrés de Jérémie

Jérémie s’est donné un modèle formé de petits carrés pour écrire les chiffres de 0 à 9. En appliquant ce modèle, il a écrit 38 ainsi.

À partir de ce nombre, au minimum combien de petits carrés, en tout, seront touchés, c’est-à-dire ajoutés, enlevés ou déplacés pour écrire 25 ?

 132. Visite de monuments

 Sur une rue, il y a neuf monuments

chacun étant éloigné du même nombre de mètres l’un de l’autre.

Naomie a parcouru 80 mètres pour aller

du premier au dernier monument et revenir au point de départ.

 Quelle est la distance entre chaque monument ?

133. Joachim signe

Joachim découpe quatre jetons et y écrit les nombres 2, 4, 5 et 7. Il place les quatre jetons dans cet ordre :

Sans déplacer les jetons, insérez un signe +, –, × ou ÷ entre les chiffres pour obtenir 10 comme résultat.

134. Pêche suspecte

Barbara est allée à la pêche. Elle dit à son frère :

« Pour connaître le nombre de poissons que j’ai dans mon sac, tu dois trouver tous les nombres de trois chiffres formés d’un 2, d’un 5 et d’un 6, puis tu dois conserver seulement les nombres qui sont divisibles par 3. Chaque nombre conservé représente un poisson. »

La pêche a-t-elle été fructueuse ?

135. Trouvailles d’Arithma

Arithma a trouvé un nombre qui est quatre fois la somme de ses chiffres.

Ce nombre est 12. En effet, la somme des chiffres de 12 est 3.

Trouvez un autre nombre qui est quatre fois la somme de ses chiffres.

136. Rencontre prévue

Marin et Cédric demeurent à 49 kilomètres l’un de l’autre.

Ils partent à pied en même temps.

Marin parcourt huit kilomètres à l’heure.

Cédric parcourt six kilomètres à l’heure.

Au bout de combien de temps Marin et Cédric vont-ils se rencontrer ?

137. Sac de pige

Dans un sac, Paul a pigé ces cinq jetons.

À l’aide d’opérations simples, combinez les cinq numéros de façon que le résultat soit 65.

138. Une digne terrienne

Ernestine est une terrienne maintenant retraitée qui a vécu au 20^e siècle. Un jour, elle a dit :

« Si je prends le nombre d’années que j’ai vécues et si je le multiplie par lui-même, j’obtiens l’année de ma naissance. »

En quelle année, Ernestine a-t-elle tenu ces propos ?

139. Cure-dents de Laurent

Laurent écrit les chiffres de 0 à 4 avec des cure-dents. Par exemple, 0 nécessite six cure-dents et 1 nécessite deux cure-dents. Laurent agence les chiffres pour former des nombres.

Quel est le plus petit nombre de trois chiffres qui nécessite 15 cure-dents ?

140. Ordre de Jacinthe

Jacinthe a placé six jetons en ordre numérique. Elle veut intercaler deux signes +, deux signes – et un signe × entre les jetons sans les déplacer.

Insérez les signes de façon que le résultat soit 4.

                                                                                                                        Solutions 141 à 150

141. Œufs de Bastien

Bastien a acheté 2½ douzaines d’œufs pour un montant de 60 louis.

Combien coûterait 1½ dizaine d’œufs ?

142. Fraction augmentée

Luce a formé 3 et 7 avec des cure-dents de même longueur comme ci-dessous. Par exemple, le cure-dents 7 nécessite quatre cure-dents. Luce écrit la fraction trois septièmes.

À partir de la fraction, déplacez deux cure-dents de façon que la fraction soit réduite à une moitié.

143. Croisés de Zoé

Dans une grille 6 × 6, Zoé écrit des chiffres et noircit des cases à la façon des mots croisés. Elle donne des indices pour trouver chaque nombre, même les nombres d’un seul chiffre.

Remplissez cette grille en plaçant un chiffre par case d'après les indices suivants.

144. Cible d’Hélène

Hélène fabrique une cible formée de trois zones.

Les points possibles par zone sont 3, 7 et 12.

Son ami a lancé neuf flèches dans la cible pour un total de 57 points.

Il a atteint la zone 3 une fois de plus que la 7.

Combien de fois l’ami a-t-il atteint chaque zone ?

145. Gain d’écus

Mathias a gagné 35 écus. 
On lui a remis des pièces de 5, de 10 et de 25 écus.

Combien y a-t-il de façons d’agencer les pièces pour avoir 35 écus ?

146. Trios de Bernard

Bernard forme des nombres avec les chiffres 3, 4 et 5. Il dit à sa sœur :

« Tu dois trouver un nombre dont les chiffres sont différents et dont le triple contient chacun de ces trois chiffres une seule fois. Ce nombre n’a pas de 4. »

Quel est ce nombre ?

147. Voisins d’Olivia

Olivia a rempli la grille ci-après avec des chiffres de 1 à 9. Elle recherche les nombres de trois chiffres qui se touchent en tous les sens. Par exemple, elle peut lire 321, 324, 358, 359 et 368.

Combien peut-on lire d’autres nombres de trois chiffres qui commencent par 3 ?

148. Une petite famille

Réginald est père de deux filles : Manon et Nina.

Il y a 6 ans, Réginald était quatre fois plus âgé que Nina

et huit fois plus âgé que Manon.

Dans quatre ans, Réginald sera trois fois plus âgé que Manon.

Trouvez l’âge de chacun.

149. Choix de cartes

Zacharie place devant lui les huit cartes ci-après. Il doit choisir deux cartes de cœur et deux cartes de trèfle parmi elles. La somme des valeurs numériques des cartes choisies doit être égale à 28.

Identifiez les cartes que Zacharie doit choisir.

150. Indices de Stella

Stella a écrit neuf lettres dans la grille. Chaque lettre représente un nombre différent. Stella veut remplacer chaque lettre par un nombre en utilisant les indices ci-après. La somme des nombres de chaque ligne, colonne et diagonale doit être égale à 51.

A : On additionne 8 à E.

B : Les deux tiers de I.

E : La moitié de (B + H).

G : On soustrait 11 de A.

Remplissez la grille.

                                                                                                                            Solutions 151 à 160

151. Cadeaux de Noël

Myriam, Noël et Julie ont reçu chacun un cadeau en argent à Noël. Deux à deux, ils ont reçu ces montants.

s Myriam et Noël : 62 pistoles

s Myriam et Julie : 77 pistoles

s Noël et Julie : 89 pistoles

Combien chacun a-t-il reçu ?

152. Tableau de Sylva

Sylva découpe 10 jetons et les numérote : 4, 5, 7, 9, 12, 15, 16, 18, 19, 25. Elle veut placer un jeton par case tout en respectant les propositions du tableau.

Distribuez les nombres dans le tableau.

153. La tête à Papineau

Marielle a commencé à faire des recherches sur Louis-Joseph Papineau un jeudi 24 mars.

Plus tard dans l’année, soit lors du prochain mois dont le 24 était un jeudi,

elle a terminé ses recherches.

Combien de mois ont été nécessaires pour ses recherches ?

154. Eustache d’Eustache

Eustache a sorti son couteau et a découpé des brindilles d’égale longueur. Il compose les chiffres de 0 à 5 au moyen de ces brindilles. Par exemple, 0 nécessite six brindilles et 1 deux brindilles.

Quel est le plus petit nombre comportant ces chiffres qui exigera 15 brindilles pour son écriture ?

155. Opérations de Livan

À l’aide d’opérations simples, Livan a représenté 7 avec les quatre chiffres ci-après. Il a écrit : 2 + 4 + (5 ÷ 5) = 7.

2      4      5      5

Représentez 5 avec ces quatre chiffres.

156. Visite d’un oncle

Alexia est née un jeudi 8 avril.

Son oncle Tancrède est venu la visiter

la veille du 8 juillet de la même année.

En quel jour de la semaine la visite a-t-elle eu lieu ?

157. Opérations doubles

Océane a choisi cinq nombres différents. Leur somme est 20 et leur produit 288.

Quels sont ces cinq nombres ?

158. Nombre inconnu

Nicole a choisi un nombre.

Si j’additionne 5 à ce nombre, la somme est divisible par 3.

Si j’additionne 6 à ce nombre, la somme est divisible par 4.

Si j’additionne 7 à ce nombre, la somme est divisible par 5.

Quel est le plus petit nombre qui satisfait aux conditions ?

159. Araignées de grand-père

Grand-père Antoine est fier de sa collection d’araignées. Il dit :

1. Si mes trois petits-fils se partageaient également les araignées, il en resterait 2.

2. Si mes cinq petites-filles se partageaient également les araignées, il en resterait 1.

3. Si mes sept neveux se partageaient également les araignées, il n’en resterait plus.

Combien y a-t-il d’araignées au minimum dans la collection de grand-père Antoine ?

160. Séries de Sammy

Sammy a écrit quatre suites de nombres. Chaque suite a été formée selon une règle différente.

1, 3, 5, 7, 9, 11, ...

 4, 5, 7, 8, 10, 11, ...

4, 7, 6, 9, 8, 11, ...

1, 5, 4, 8, 7, 11, ...

La somme des termes du 7^e rang de ces quatre suites est 46. Quels sont ces termes ?

                                                                                                                         Solutions 161 à 170

161. Tableau de Louise

Louise a écrit sept chiffres dans ce tableau. On peut lire plusieurs nombres de trois chiffres en suivant les lignes d’un cercle à l’autre.

Trouvez un nombre entre 100 et 700 dont la somme des chiffres est 19.

162. Belle date

Samantha est née un 3 mars. Elle a découpé six jetons et les a marqués du chiffre 3. Elle place des signes entre les jetons pour produire des égalités. Toutefois, elle peut accoler deux jetons.

À l’aide d’opérations simples, représentez 75 avec ces six jetons.

163. Castors au travail

Un groupe de castors a abattu 130 épinettes et sapins au cours d’un mois.

Le nombre d’épinettes abattues est le triple du nombre de bouleaux, augmenté de 3.

Le nombre de sapins abattus est le double du nombre de bouleaux, augmenté de 7.

Combien le groupe de castors a-t-il abattu d’arbres de chacune des trois espèces ?

164. Triangle d’Anna

Anna a écrit les nombres impairs consécutifs en un triangle. La somme des nombres de la quatrième rangée est 64.

Quelle est la somme des nombres de la 10^e rangée ?

165. Mois d’avril

Marie-Avril prend la feuille d’un calendrier d'un mois d’avril dans lequel le 16 et le 23 ont été effacés.

Trouvez six nombres disposés en un rectangle 2 × 3 dont la somme est 111.

166. Incursion romaine

Ursule ne connaît que les chiffres romains pour écrire les nombres. Elle a représenté 8, soit VIII, en utilisant cinq bâtonnets.

Comment Ursule peut-elle représenter 9 en chiffres romains avec six bâtonnets ?

167. Assiettes d’Aaron

Aaron prend six assiettes de collection qui sont déjà numérotées 2, 4, 5, 7, 8 et 9. Il doit disposer cinq des six assiettes dans les cases libres de façon que la somme des trois nombres formés soit 91.

Quelle assiette ne sera pas utilisée ?

168. Billes de Martin

Martin a un sac de 80 billes. Il dispose ses billes de telle manière qu’il y a deux billes de plus d’une rangée à l’autre. Les quatre premières rangées sont montrées. Quand il a terminé, il remet dans son sac les billes qui forment la dernière rangée incomplète.

À la fin, combien le sac contiendra-t-il de billes ?

169. Cléo découpe

Cléo a découpé quatre jetons et écrit un chiffre sur chacun.

Trouvez les nombres pairs dont le triple contient trois de ces quatre chiffres une seule fois.

170. Oubli de Sara

Sara a transcrit l’égalité ci-après. Elle a oublié d’écrire un nombre dans le cercle demeuré vide.

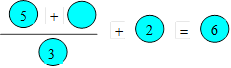
Trouvez le nombre qui va faire en sorte que l’égalité soit vraie.

                                                                                                                            Solutions 171 à 180

171. Torticolis de Julien

Julien a écrit son prénom dans la figure ci-après. Il désire remplacer chaque lettre par un nombre. La somme dans chaque rangée de deux cases colorées voisines est donnée en leur centre.

Quelle est la valeur de J + U + L + I + E + N ?

172. Erreur d’Étienne

Étienne a additionné les trois nombres ci-après. Malheureusement, le résultat est faux.

Remplacez trois chiffres chacun par un 1 de façon que la somme soit 1446.

173. Égalités de Juliane

Dans les cases, Juliane veut placer les chiffres de 1 à 9, sauf 4 et 5. Deux cases libres accolées doivent accueillir un nombre de deux chiffres.

Distribuez les sept chiffres de façon que les deux égalités soient vraies.

174. Carrés de Danielle

Danielle a écrit les chiffres de 5 à 9 comme ci-après au moyen de petits carrés.

Trouvez le plus grand nombre de trois chiffres différents qui utilisent 31 carrés pour son écriture.

175. Étoiles de Joachim

Joachim aimerait bien que son école adopte la semaine de quatre jours. En attendant, il écrit JEUDI à la suite. Il insère un astérisque entre chaque lettre et trois astérisques entre chaque JEUDI.

J*E*U*D*I***J*E*U*D*I***J*E*U*D*I***J...

Quelle lettre sera écrite immédiatement après le 50^e astérisque ?

176. Jetons d’Olivier

Olivier a préparé cinq jetons numérotés comme ci-après. Il les a placés sur la table. Sans déplacer les jetons, il faut écrire un signe + ou – entre eux de façon que le résultat soit 2.

Placez les signes + et – entre les jetons.

177. Nazaire au Chili

Depuis le début de l’année 2011 dont le premier janvier était un samedi, Nazaire rêvait à ce jour qui était le 100^e de l’année. En effet, il partait en voyage pour le Chili.

En quel jour de la semaine, Nazaire est-il parti en voyage ?

178. Choix de Jonas

Jonas choisit deux nombres.

L’un est cinq fois plus grand que l’autre.

Si, de la moitié du grand, l’on soustrait le double du petit, le résultat est 3.

Quels sont ces deux nombres ?

179. Fraction de Ginette

Ginette découpe cinq jetons et les numérote de 3 à 7. Parmi ceux-ci, elle prend quatre jetons dont la somme des numéros est 19.

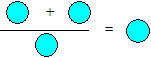
Disposez ces quatre jetons sur le tableau de façon que l’égalité soit vraie.

180. Perturbation royale

C’est jour de fête dans la ruche : le couronnement de la reine. Il y a cependant en retrait des visiteurs inopportuns. Ce sont des fourmis et des papillons appelés fausses teignes. Il y a deux fois plus de fourmis que de papillons. Après le départ de neuf fourmis, il y a encore huit fourmis de plus que de papillons.

Combien y a-t-il de visiteurs inopportuns ?

                                                                                                                       Solutions 181 à 190

181. Douzaines de Sébastien

Sébastien a dessiné le tableau ci-après. Il veut y écrire quatre nombres de deux chiffres.

• La somme des quatre nombres doit être 144.

• Les chiffres de 1 à 8 apparaissent chacun une seule fois.

• Le deuxième nombre est le triple du premier.

• Le troisième nombre est le deuxième augmenté de 5.

Quel est le quatrième nombre ?

182. Monnaie de Jasmin

Jasmin a déposé 13 pièces dans une tirelire. Le montant total est de 235 florins. Il comprend des pièces de 5, de 10 et de 25 florins.

Combien de pièces de chaque valeur Jasmin a-t-il déposé ?

183. Des bons comptes

Isaac a préparé cinq jetons sur lesquels il a écrit autant de nombres.

Placez un signe +, –, × ou ÷ entre les jetons sans les déplacer. Le résultat doit être égal à 315.

184. Mai de Flavius

Flavius prend une feuille de calendrier d’un mois de mai. Il délimite des carrés 3 × 3 qui contiennent neuf nombres. Il y a un carré dont la somme des nombres des quatre coins est 72.

Quel est le nombre du milieu de ce carré ?

185. Temps qui passe

Deux amis ont une conversation.

Émilie dit : « Je suis née un jeudi le 7 juin 2001. »

Danny reprend : « Moi, je suis né 100 jours plus tard. »

Quel jour de la semaine Danny est-il né ?

186. Poires de Laura

Laura cultive des variétés de poires spéciales.

Les unes poussent en grappes de deux et les autres en grappes de trois.

Laura a cueilli 37 grappes de poires pour un total de 97 poires.

Combien Laura a-t-elle cueilli de grappes de deux, puis de trois poires ?

187. Duo d’Hector

Hector choisit deux nombres.

Ceux-ci sont tels que le plus grand diminué de 12

est égal au petit augmenté de 25.

La somme de ces nombres est 89.

Quels sont ces deux nombres ?

188. Diagramme de Sara

Dans le tableau ci-après, Sara a donné certaines propriétés des nombres à gauche et en haut.

Dans les cases, placez les nombres 10, 11, 15, 16, 17, 24, 30, 35 et 40 tout en respectant les propriétés données.

189. Les 7 de Sophie

Sophie a inscrit le numéro 7 sur cinq jetons et a placé ceux-ci en une rangée.

Insérez un signe +, –, × ou ÷ entre les jetons de façon que le résultat soit 13.

190. Tout en neuf

François a multiplié des nombres composés de 9, puis il a écrit à droite le résultat.

D’après ces données, quel est le résultat de 99 999 × 99 999 × 99 999 ?

                                                                                                                            Solutions 191 à 200

191. Coccinelles de Bob

Bob prend six coccinelles et les numérote comme ci-après. Il prend des groupes de trois coccinelles et additionne leur numéro.

Combien y a-t-il de trios de coccinelles dont la somme des numéros est supérieure à 17 ?

192. Carton de Nicolas

Sur un carton, Nicolas a écrit des nombres inférieurs à 99.

Combien y a-t-il de paires de nombres dont la somme est 99 ?

193. Pommes de Lucia

Lucia veut partager des pommes successivement entre 2, 3, 4 et 5 enfants. Elle a cinq sacs de pommes qui contiennent ces quantités.

Combien de sacs pourront être partagés également ?

194. Saison fructueuse

Gabriel est fier de sa saison au hockey. Il dit à son professeur de mathématiques :

- Devine combien j’ai compté de buts cette année.

Je multiplie le nombre de buts par 3.

Je soustrais 5.

Je divise par 2.

J’obtiens 8.

Combien Gabriel a-t-il compté de buts ?

195. Étoiles filantes

Célestin compte les étoiles dans le ciel ou dans sa tête, selon les moments. Il écrit trois nombres dont la somme est 1991.

247 + 783 + 961 = 1991

Rayez trois chiffres dans les trois premiers nombres. Remplacez chacun de ces chiffres par 5 pour que la somme soit 1559.

196. Nombre de Jonas

Jonas a choisi un nombre impair de trois chiffres.

La somme des chiffres est 15.

Le deuxième chiffre est inférieur de 4 au troisième.

La somme des deux derniers chiffres est le double du premier.

Quel est ce nombre ?

197. Au cinéma

Louise a vu 27 films au cinéma l’année dernière. Elle a noté ceci.

• Au deuxième trimestre, j’ai vu deux fois plus de films qu’au premier trimestre.

• Au troisième trimestre, j’en ai vu trois fois moins que pendant les deux premiers trimestres.

• Au quatrième trimestre, j’ai vu deux films de plus qu’au troisième trimestre.

Combien Louise a-t-elle vu de films au premier trimestre ?

198. Une grille élargie

Fernand a écrit les nombres de 1 à 20 dans la grille ci-après. Il veut se rendre jusqu’à 40 en élargissant la grille vers la droite et en continuant selon le même modèle.

Dans quelle colonne Fernand pourra-t-il écrire 40 ?

199. Une devinette

Je pense à un nombre.

Je le multiplie par 6.

J’obtiens un nombre entre 114 et 143.

J’additionne 10 au résultat.

J’obtiens un nombre entre 143 et 160.

Quel est le nombre pensé ?

200. Trèfles variables

Nicolas a disposé 10 trèfles en une addition comme ci-après. Il donne à chaque trèfle une valeur différente variant de 0 à 9. Le premier nombre est 652.

Quelle est la somme sachant que sa dizaine est 8 ?

                                                                                                               Solutions 201 à 210

201. Signes d’Henri

Henri a découpé quatre jetons et les a numérotés comme ci-après. Il désire placer un signe +, –, × ou ÷ entre les jetons sans en changer l’ordre.

Insérez un signe entre les jetons de façon que le résultat soit 8.

202. Un surplus

Martine a écrit 12 nombres dans la grille ci-après. Il faut additionner deux par deux les nombres de la grille de façon à obtenir chaque somme : 12, 18, 24, 30 et 36. Un nombre ne peut être utilisé qu’une seule fois. À la fin, il restera deux nombres.

Quels sont ces deux nombres ?

203. Marraine de Sylvia

Le 24 janvier 2015, il faisait un froid de canard accompagné d’un beau soleil.

C’est ce samedi-là que Sylvia a choisi pour atterrir dans ce monde.

Sa future marraine était à la chaleur dans le Sud. Elle revint le 24 mars.

Quel était le jour de la semaine quand la future marraine revint ?

204. Chiffres d’Élise

Élise a préparé une grille dans laquelle elle a écrit des chiffres. Elle a effacé les chiffres. On peut les retrouver en écrivant les nombres donnés jusqu’à ce que la grille soit remplie. Les nombres d’un chiffre ne sont pas donnés.

Remplissez la grille.

205. Marche de Koralie

Koralie doit partir de 9 et se rendre jusqu’à 2. À la place de chaque étoile, elle insère un signe +, −, × ou ÷, chacun une seule fois.

9 « 8 « 7 « 5 «2

Insérez les signes de façon que le résultat soit 15.

206. Nombres de Nancy

Nancy a choisi deux nombres.

Ils sont tels que le plus grand diminué de 21

est égal au double du petit augmenté de 5.

La somme de ces nombres est 119.

Quels sont ces deux nombres ?

207. Denis calcule

Denis a représenté 109 avec quatre 1 et quatre 4. Voici ce qu’il a écrit :

41 + 41 + 41 − 14 = 109

Représentez 200 avec quatre 1 et quatre 4.

208. Somme de Bertrand

Bertrand veut placer chacun des chiffres de 1 à 7 une seule fois, sauf le 4, dans les six cases de façon que la somme soit vraie. Le premier nombre est inférieur de 15 au deuxième.

Distribuez les six chiffres.

209. Autos d’Alexane

Alexane a numéroté ses huit petites autos et les a placées en une seule rangée avec les numéros en ordre croissant.

w La différence entre chaque numéro est identique.

w La somme des numéros de la 2^e auto et de la 5^e auto est 34.

w La somme des numéros de la 3^e auto et de la 7^e est 46.

Quel est le numéro de la 8^e auto ?

210. École Frère-André

Autrefois, Étienne était inspecteur d’écoles. Chaque printemps, il visitait toutes les écoles de son secteur. Un jour, il visita l’école Frère-André. Il y avait trois classes dans cette école. Dans la classe B, il y avait trois élèves de moins que dans la classe A. Dans la classe C, il y avait quatre élèves de plus que dans la B. Il y avait 94 élèves en tout.

Combien y avait-il d’élèves dans chacune des classes ?

                                                                                                                           Solutions 211 à 220

211. Âges en lignes

Les âges de Benoît, le plus jeune, et de Carmel sont sur deux lignes voisines de la grille ci-après. Si on additionne les âges, on obtient 36. La différence d’âge est la plus grande possible.

Quels sont les âges de chacun ?

212. Calendrier original

Un calendrier est formé de cinq mois de 73 jours chacun.

Les mois sont : mars, avril, mai, juin et juillet.

Si le 23 mars était un vendredi, quel jour de la semaine serait le 23 avril de la même année ?

213. Blocs de France

France a dessiné 24 blocs et y a inscrit les nombres de 1 à 24.

Trouvez un carré de quatre nombres dont la somme est 78.

214. Émilia croque

Émilia prépare six petits sacs de noisettes. Le premier contient 2 noisettes, le second 3 noisettes et ainsi de suite jusqu’au sixième sac qui en contient 7. Elle dit à sa nièce :

« Place les petits sacs sur les cases ci-après. Deux cases accolées reçoivent un nombre de deux chiffres. Il te faut placer les sacs de façon que le troisième nombre soit supérieur de 26 au premier et supérieur de 7 au deuxième. »

Disposez les six sacs de noisettes de façon que la somme soit 126.

215. Nombres spéciaux

Andrée a déniché deux nombres qu’elle veut mettre en valeur.

Les deux nombres sont tels que le plus grand diminué de 30

est égal au double du petit.

La somme de ces nombres est 84.

Quels sont ces deux nombres ?

216. Brocolis de Clairette

Clairette note la quantité de légumes qu’elle et sa famille ont consommés pendant quatre mois.

s En février, ils ont consommé deux fois plus de brocolis qu’en janvier.

s En mars, ils ont consommé six brocolis de moins qu’en février.

s En avril, ils ont consommé deux fois moins de brocolis qu’en mars.

Clairette dit en secret à sa fille : « Nous avons mangé 16 brocolis en avril. »

Combien cette famille a-t-elle consommé de brocolis en janvier ?

217. Un esprit de nombre

Je pense à un nombre.

Je le multiplie par 5.

J’obtiens un nombre entre 75 et 95.

J’additionne 4 au résultat.

J’obtiens un nombre entre 84 et 94.

Quel est le nombre pensé ?

218. Vente de balayeuses

En ce moment, Juliette est dans un des 23 appartements du 5^e étage d’un immeuble. Les numéros partent de 501 et s’arrêtent à 523. Juliette est en train de faire la promotion d’une balayeuse.

1. Elle est dans un appartement dont le chiffre des centaines est inférieur à celui du dernier chiffre.

2. Elle est dans un appartement dont la somme des chiffres est impaire.

3. Elle n’est pas dans les appartements 506, 517 ou 519.

Dans quel appartement Juliette est-elle ?

219. Distraction de Charlotte

Dans l’égalité ci-après, Charlotte doit placer un signe +, –, × ou ÷ à la place d’un petit carré de façon que l’égalité soit vraie. Le résultat de chaque membre de l’égalité est soit 33, soit 36, soit 39.

8 ■ 5 ■ 4 = 11 ■ 3 ■ 3

Rendez cette égalité vraie.

220. Des fermes laitières

Quatre cultivateurs dont les terres sont voisines ont voulu m’indiquer le nombre de vaches qu’ils possédaient.

• Kevin a neuf vaches de plus que Jeanne.

• Lydia a huit vaches de plus que Kevin.

• Marco a sept vaches de plus que Lydia et a deux fois plus de vaches que Jeanne.

Combien Jeanne a-t-elle de vaches ?

                                                                                                                Solutions 221 à 230

221. Allumettes de Guy

Guy a représenté les chiffres de 1 à 6 avec des allumettes. Par exemple, le 1 nécessite deux allumettes. Guy cherche deux nombres dont la somme est 54 et dont la différence est inférieure à 10.

Trouvez les deux nombres qui utilisent 17 allumettes.

222. Concours de maths

Jean-Pierre a compilé les résultats obtenus par 55 élèves lors d'un concours régional de mathématiques. Il a partagé les résultats en quatre groupes : W, X, Y et Z.

1. Le groupe X comprend six élèves de plus que le W.

2. Le groupe W comprend deux élèves de plus que le Y.

3. Les groupes X et Z ont ensemble 27 élèves.

Combien y a-t-il d’élèves dans chacun des groupes ?

223. Distribution d’Emma

Emma a distribué les chiffres de 1 à 6 dans l’addition ci-après. La somme est 102.

Intervertissez le moins possible de paires de chiffres de façon que la somme soit 111.

224. Division d’Azalée

Azalée dessine cinq cases comme ci-après. Les cases accolées peuvent recevoir un nombre de deux chiffres.

Placez les chiffres 1, 2, 3, 4 et 5 dans les cases vides de façon que l’égalité soit vraie.

225. Opérations de Jérémie

Jérémie s’amuse à combiner des chiffres identiques avec des opérations simples de façon que le résultat soit 24. Par exemple, il a écrit :

 3 × 3 × 3 − 3 = 24

Représentez 24 successivement avec quatre 4, quatre 5 et quatre 6.

226. Pierre et Margot

Pierre et Margot multiplient leur âge respectif. Le résultat est 448.

Dans quatre ans, Pierre aura le double de l'âge de Margot.

Quels sont les âges de Pierre et de Margot ?

227. Tuiles de Chanceuse

Chanceuse découpe huit jetons et les numérote 1, 2, 3, 4, 6, 7, 8 et 9. Elle désire placer ces jetons dans les huit tuiles colorées, tout en respectant les trois égalités.

Disposez les huit jetons.

228. Cueillette de cerises

La cueillette des cerises est terminée chez le père Philon. En visitant les cerisiers de son père, François a remarqué qu’il restait le même nombre de cerises dans chaque arbre. De plus, ce nombre de cerises par arbre est aussi le nombre total de cerisiers. Après avoir fait quelques calculs, François a trouvé qu’il restait en tout entre 306 et 336 cerises dans les arbres.

Combien y a-t-il de cerisiers dans ce verger ?

229. Égalité de Simone

Simone a écrit trois nombres dans chaque membre d’une égalité.

Remplacez chaque étoile par un signe +, –, × ou ÷ pour que l’égalité soit vraie

230. Découverte d’Ariane

Ariane a découvert une disposition remarquable de nombres. Quand l’unité du premier nombre décroît, l’unité du résultat croît et s’acoquine avec des 8.

En vous basant sur ces résultats, trouvez à quoi est égal 987 654 321 × 9.  

                                                                                                                          Solutions 231 à 240

231. Téléphone des Électron

Benjamin Électron ne voulait pas donner son numéro de téléphone à un de ses nouveaux amis. Il préféra lui donner ces six indices.

1. Les sept chiffres sont différents et il n’y a pas de zéro.

2. Le deuxième chiffre a trois unités de plus que le premier.

3. Le troisième chiffre a une unité de plus que le deuxième.

4. Le quatrième chiffre a trois unités de moins que le premier.

5. Le cinquième chiffre est le double du sixième.

6. Le septième chiffre a une unité de plus que le cinquième.

Découvrez le numéro de téléphone de la famille Électron.

232. Roubles de Guylaine

Dans une urne, il y a des pièces de 1, 5, 10 et 25 roubles. Chacune de leur côté, Laura et Guylaine ont le droit de piger 17 pièces qui totalisent 100 roubles.

s Guylaine prend moins de pièces d’un rouble que Laura.

s Guylaine prend plus de pièces de 5 roubles que Laura.

s Laura et Guylaine prennent le même nombre de pièces de 10 roubles.

s Laura et Guylaine prennent au moins une pièce de chaque valeur.

Combien Laura et Guylaine devront-elles piger de pièces de chaque valeur ?

233. Serpent de Thérèse

Thérèse a écrit les nombres de 1 à 16 en serpent comme ci-après. Elle désire continuer à écrire les nombres jusqu’à 100.

Dans quelle position se trouvera 28 ?

234. Impairs de Gaston

Gaston cherche deux nombres de trois chiffres différents.

Le double de ces nombres doit contenir

trois des quatre chiffres ci-après une seule fois : 2, 4, 7 et 8.

Quels sont les deux plus grands nombres impairs ?

235. Montréal naît

Paul Chomedey de Maisonneuve est né le 15 février 1612 à Troyes en France.

Il a fondé Montréal le 17 mai 1642.

Pendant la première messe en sol canadien,

un Amérindien s’interrogeait sur l’âge du nouveau gouverneur.

À ce moment, pendant combien de mois ayant un N et un V Maisonneuve avait-il vécu ?

236. Chiffres de Jade

Jade a écrit quatre nombres dont la somme est 1745. Son petit frère a remplacé deux de ces nombres par des étoiles. Ces deux nombres ont les mêmes chiffres. Aucun de ces chiffres n’appartient aux deux nombres connus de trois chiffres.

Quels sont ces deux nombres ?

237. Fête au chalet

Cinq amis sont réunis dans un chalet. L’hôtesse m’a indiqué l’âge de chacun. Dans ce groupe, il y a un intrus, car son âge possède une propriété différente des quatre autres.

 Qui est l’intrus ?

238. Année vedette

Marcelle a représenté 7 avec les chiffres de 2013. Elle a écrit :

(20 + 1) ÷ 3 = 7

Avec les chiffres de 2013 pris chacun une seule fois et sans utiliser les signes + et – devant 0 et 1, représentez successivement 1, 2, 4 et 5.              

239. Courriels de Murielle

À cause de ses performances comme gardienne de but au hockey, Murielle a reçu des courriels de félicitations. Elle a imprimé tous les messages. Elle voudrait faire des groupes de 9, mais il manque deux messages pour le dernier groupe. Si elle place un message de plus par groupe et fait un groupe de moins, tous les messages sont pris.

Combien Murielle a-t-elle reçu de courriels au minimum ?

240. Flèches de Maxime

Maxime lance des flèches sur une cible de forme carrée comme il est illustré. La mesure du centre du grand carré jusqu'à sa bordure extérieure est de 10 centimètres répartis également entre les points d’intersection avec les côtés des carrés. À chaque lancer de flèches, Maxime atteint toujours la cible.

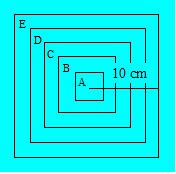
Dans ces conditions, quelle est la probabilité d'atteindre la zone E ?

FIN