|
***************
Problèmes 1 à 50
***************
1. Débrouillerie de dés
Le tableau suivant comprend 25 dés. Noircissez certains dés pour qu’il
en reste un seul marqué 5 sur chaque ligne et dans chaque colonne.

Indiquez
la position de chaque dé qui reste.
2.
Tirelire de Léa
Dans sa tirelire,
Léa a 16 pièces de monnaie : ce qui lui donne exactement 100 centimes.
Elle a au moins une pièce de chaque valeur : 1 centime, 5 centimes, 10
centimes et 25 centimes.
Trouvez
le nombre de pièces de chaque valeur.
3.
Marge de Samuel
Samuel a attribué
une valeur à chacune des lettres suivantes. Il a formé un mot de cinq lettres
qui vaut 10 points, soit MARGE.
En utilisant
une lettre une seule fois, trouvez un mot de cinq lettres qui vaut 11 points.
4.
Nombres croisés
Remplissez cette
grille en plaçant un chiffre par case.
A. J’ai un 2, un 5 et un 7. – La somme de mes chiffres est 15.
B.
La somme de mes chiffres est 4. – Je suis entre 430 et 439.
C.
Je suis le triple de 216. – Je suis le plus petit carré pair non nul.
D.
Je suis pair. – Je suis entre 800 et 900.
E.
Je suis entre 400 et 500. – Je suis un multiple de 17.
F.
La somme de mes chiffres est 9. – Je suis le quadruple de 127.
G.
Je suis entre 50 et 60. – J’ai trois chiffres identiques.
H.
La somme de mes chiffres est 9. – La somme de mes chiffres est 7.
I.
Je suis impair. – La somme de mes chiffres est 14.
J.
La somme de mes chiffres est 17. – Je suis la racine carrée de 25.
K.
Je suis entre 70 et 80. – La somme de mes chiffres est 8.
L.
La somme de mes chiffres est 17. – J’ai deux chiffres identiques.
5. Partage de cœurs
William a distribué des cœurs dans
cette grille.
|
©
© |
© |
©
© |
©
©
© |
|
© |
©
©
©
© |
©
©
© |
© |
|
©
© |
©
© |
©
©
©
© |
© |
|
© |
©
©
© |
©
©
© |
©
©
© |
Partagez la grille en quatre parties de même forme et de
même grandeur. Chaque partie doit contenir le même nombre de cœurs.
6.
Cadran de Gabriel
Un beau lundi,
Gabriel regarde son cadran d’horloge. Il marque 13 : 27. Au début de l’après-midi
le lendemain, il note que son cadran marque encore 13 : 27.
Entre
ces deux marques, combien de fois la combinaison des chiffres 1, 2, 3 et 7
est-elle apparue sur le cadran ?
7.
Monnaie de Florence
Florence prend
sept pièces de monnaie et les place comme ci-après. Elle réalise ainsi cinq
rangées de trois pièces.
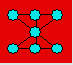
Ajoutez deux
pièces de monnaie pour obtenir 10 rangées de trois pièces.
8.
Liens de parenté
Ces
quatre symboles expriment chacun un lien de parenté entre deux personnes :
Ä
: est le père de
Å : est la mère
de É
: est le frère de Ì
: est la sœur de.
Voici
les liens de parenté entre sept personnes :
Jeanne Å
Réjean
Jacques Ä Denise
Martine
Ì Réjean
Gilles É
Denise
Luc Ä Martine
Réjean É Jacques
Qui sont les
grands-parents ?
9.
Domino de Nathan
Nathan a disposé
des lettres de DOMINO comme suit. Il pose son crayon sur le D et trace un chemin
en passant par les lettres de DOMINO.
D
O
. O
M
. M . M
I
. I . I . I
N
. N . N
O
. O
Combien de
chemins différents Nathan peut-il tracer ? Il y en a plus de 12.
10.
Nature en folie
Vincent,
Gabriel et Marianne ont composé un texte respectivement sur la pluie, le vent
et le soleil. Ils ont obtenu 75, 80 et 85 points.
1.
L’enfant qui a composé le texte sur la pluie a obtenu 80.
2.
Vincent a obtenu une meilleure note que Marianne.
3.
Gabriel n’a pas traité du vent.
4.
Le texte sur le soleil n’est pas de Vincent.
5.
Marianne a eu une meilleure note que Gabriel.
Trouvez le sujet traité par chaque
enfant et la note obtenue.
|
|
Vincent |
Gabriel |
Marianne |
|
Sujets |
|
|
|
|
Notes |
|
|
|
11.
Quatrième carré
En vous basant sur
les trois premiers dessins, complétez le quatrième carré.
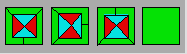
12.
Triangle de Carmen
Carmen a écrit d’abord
les nombres de 1 à 16 en un triangle comme ci-après. Puis elle a continué l’écriture
selon le même modèle en reprenant le nombre de la fin d’une ligne au début
de l’autre ligne.
|
1
1
2
2
3 4
4
5 6 7
7
8 9 10 11
11
12 13 14 15 16 |
Quel nombre
est au milieu de la neuvième ligne ?
13. Figure de
Rosalie
Rosalie a dessiné la figure suivante.
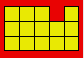
Partagez cette
figure en deux parties de même forme et de même grandeur.
14.
Grille de Clara
Dans la grille,
Clara a écrit neuf nombres. Elle désire retrouver des chiffres différents sur
chaque ligne, dans chaque colonne et dans chaque diagonale.
|
72 |
|
16 |
|
50 |
|
|
|
|
|
|
|
49 |
|
38 |
|
27 |
|
|
|
|
|
|
|
16 |
|
50 |
|
94 |
Complétez la
grille avec des nombres de 10 à 100.
15. Initiale de
Sara
Sara a écrit l’initiale de son prénom sept
fois dans ce triangle.
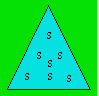
Tracez deux
triangles pour que chaque S soit isolé de chacun des autres.
16.
Mois à numéros
Chaque
mois correspond à un nombre.
MAI
+ JUIN = JUILLET
AVRIL
+ AOÛT = SEPTEMBRE
MARS
+ MARS = NOVEMBRE
À
quel nombre correspond DÉCEMBRE ?
17.
Boules en prison
Au jeu de billard,
les 15 boules sont placées en un triangle comme ci-après. Les trois boules du
centre sont prisonnières.

Au pays des
géants, on joue au billard avec 45 boules qu’on dispose aussi en un triangle.
Combien de boules sont alors prisonnières ?
18.
Fruits d’Olivier
Dans ce rectangle,
Olivier a dessiné six fruits différents.
|
pomme |
pêche |
poire |
raisins |
pomme |
fraise |
|
cerise |
raisins |
fraise |
cerise |
pomme |
cerise |
|
fraise |
pêche |
pêche |
fraise |
poire |
raisins |
|
poire |
pomme |
cerise |
poire |
raisins |
pêche |
Découpez ce
rectangle en quatre parties telles que chaque partie contient les six fruits
différents.
19.
Des cadeaux précieux
Alice, Marguerite
et Prudence possèdent chacune une pierre précieuse : un diamant, un rubis
et un saphir. Elles les donnent à Bruno, Rouen et Francis.
1.
Bruno n’a pas reçu le saphir.
2.
Alice n’a pas de diamant.
3.
Rouen a obtenu le rubis ou le saphir
4.
Marguerite possède un rubis ou un saphir.
5.
Francis n’a pas eu de cadeau de Marguerite, car il ne veut pas de rubis.
6.
Prudence a donné sa pierre précieuse à Francis.
Qui a donné et
qui a reçu chacune des pierres précieuses ?
|
Donatrices |
|
|
|
|
Pierres |
|
|
|
|
Récepteurs |
|
|
|
20. Noirs et
blancs
Coralie a tracé les quatre figures de gauche.
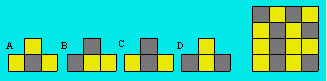
Assemblez ces figures pour former le carré de droite.
21.
Billes de Maïka
Maïka possède
huit billes de même apparence. Sept billes ont le même poids mais la huitième
est plus légère que les autres. Maïka veut identifier la bille la plus
légère en effectuant deux pesées sur une balance à plateaux.
Comment
doit-elle procéder ?
22. Nombres
croisés
Remplissez cette grille en plaçant un chiffre
par case.
A. J’ai deux 2 et deux 3. – Mon carré se termine par
moi.
B.
Mon premier chiffre est le double du deuxième et mon deuxième le double du
troisième. – La somme de mes chiffres est 15.
C.
Si on me multiplie, on me retrouve. – J’ai deux 4 et deux 5.
D.
La somme de mes deux premiers chiffres est égale à la somme de mes deux
derniers.
E.
Je suis le triple de 11, de 12 ou de 13. – J’ai un 2 et deux 9.
F.
La somme de mes chiffres est 13. – La somme des chiffres de mon carré est
égale à moi.
G.
La somme de mes chiffres est 10. – Je suis le double de 18, de 28 ou de 38.
H.
Je suis le double de 17, de 27 ou de 37. – J’ai deux 5 et un 9.
I.
J’ai deux 2, un 4 et un 6. – Mon cube est le double de mon carré.
J.
Je suis impair. – J’ai les chiffres de 9504 dans le désordre.
K.
J’ai un 2, un 4 et deux 7.
L.
J’ai deux 5 et un 8. – J’ai deux chiffres identiques.
23.
Jeu de basse-cour
Trois poules se
reposent dans les cases A, B et C. À l’opposé, trois lapins sont dans les
cases I, J et K. Il faut déplacer les animaux jusqu’à ce que chaque poule
ait échangé sa place contre un lapin de même numéro.

Prenez six
jetons. Marquez-les P1, P2, P3, L1, L2 et L3. Placez-les sur les cases
indiquées. Maintenant glissez les jetons sur les cases libres. Trouvez un
chemin.
24.
Mot bien caché
L’autre
jour, Sofia a demandé à cinq de ses amis de deviner un mot de cinq lettres
différentes qu’elle avait choisi.
Dérek
a dit VÊTIR.
Mathias
a dit CALME.
Maude
a dit LAMPE.
Tommy
a dit AMPLE.
Éva
a dit ÉLIMA.
Sofia a alors répondu : Aucun n’a
trouvé le bon mot. Toutefois, Dérek a deux bonnes lettres qui sont en bonne
position. Les quatre autres ont chacun quatre bonnes lettres mais aucune n’est
dans la bonne position.
Quel
mot a choisi Sofia ?
25.
Pépites d’or
Antoine a tracé
une grille 5 ´
5. Dans une case, il a placé un autobus qui, selon lui,
transporte des pépites d’or. Il engage quatre cavaliers pour surveiller l’autobus.
Chaque cavalier, comme aux échecs, se déplace en L.
Disposez les
quatre cavaliers de telle manière que seule la case occupée par l’autobus ne
puisse pas être prise. Les cases où seront placés les cavaliers sont
considérées comme prises.
26.
Trèfles de Noémie
Noémie a dessiné
29 trèfles dans cette grille. Elle pose un pion dans la case inférieure gauche
; puis elle le déplace en tout sens sauf en diagonale. Quand le pion atteint
une case marquée d’une flèche, il suit le sens de celle-ci.
|
§ |
§ |
§ |
ß |
§ |
§ |
|
Þ |
§ |
§ |
§ |
§ |
§ |
|
§ |
§ |
§ |
§ |
§ |
§ |
|
§ |
Þ |
§ |
Ü |
§ |
§ |
|
§ |
§ |
Ý |
§ |
§ |
§ |
|
l |
§ |
§ |
Ý |
§ |
§ |
Trouvez un
chemin que le pion devra suivre pour cueillir les 29 trèfles.
27. Tout d’un
trait
Laurence veut reproduire cette figure d’un
trait continu, soit sans lever le crayon.

De quel point devra-t-elle partir ?
28. Addition de Justin
Justin a écrit une addition en dessinant des objets. Chaque objet
est mis pour un chiffre différent. Par exemple, %
pourrait être égal à 2, mais ce n’est pas le cas.
|
(
% & :
+ (
% & &
*
( % & |
Quel objet a
la plus grande valeur ?
29.
Carré de cartes
Dans un jeu de
cartes, Charlotte prend 16 pièces : les quatre 7, les quatre 8, les quatre
9 et les quatre 10. Elle veut disposer les 16 cartes dans un carré 4 ´
4 de telle manière qu’il y ait un 7, un 8, un 9 et un
10 dans chaque rangée horizontale, verticale et diagonale. De plus, il doit y
avoir une carte de chaque couleur (pique, cœur, carreau, trèfle) dans ces
mêmes rangées. Six indices sont donnés dans la grille.
Distribuez les 16 cartes.
30. Casse-tête de
Mathis
Mathis a découpé sept pièces ayant la forme
suivante.
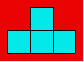
Dans cette grille, placez les pièces en
excluant les cases noires.
31.
Chiffres en ordre
Je
suis un nombre de quatre chiffres différents.
Mon
premier chiffre est dans 8352.
Mon
deuxième est dans 7236.
Mon
troisième est dans 9652.
Mon
quatrième est dans 6373.
Aucun
chiffre de mon tout n’est dans 6790.
Qui
suis-je ?
32.
En manque
Trouvez le nombre
qui devrait remplacer le point d’interrogation.

33.
Chasse aux insectes
Benjamin, Rose et
Maude ont installé leur propre piège lumineux. Ils ont utilisé chacun une
ampoule de 10, 15 et 20 watts.
1.
Les trois enfants ont attiré au total 27 coléoptères et 23 papillons de nuit.
2.
Sans utiliser une ampoule de 20 watts, Maude a capturé le plus grand nombre de
papillons de nuit, soit 10.
3.
Rose a capturé le même nombre de papillons de nuit que Benjamin de
coléoptères.
4.
L’enfant qui a pris huit papillons de nuit avait une ampoule de 15 watts.
5.
L’ampoule la moins puissante a permis d’attirer sept coléoptères.
6.
Benjamin a capturé le plus petit nombre de papillons de nuit avec une ampoule
supérieure à 15 watts.
Trouvez le nombre de papillons de nuit,
le nombre de coléoptères capturés par chaque enfant et la puissance de l’ampoule
de chacun.
|
Enfants |
|
|
|
|
Papillons
de nuit |
|
|
|
|
Coléoptères |
|
|
|
|
Watts |
|
|
|
34.
Chaînes de monnaie
Sur une grille 7 ´
7, Emma dépose 10 pièces de monnaie réparties en 1 ¢,
5 ¢, 10 ¢ et 25 ¢.
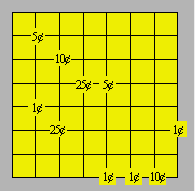
Reliez par un
trait de crayon chaque couple de pièces ayant la même valeur en suivant les
lignes tracées. Il n’est pas permis de passer sur une autre pièce et de
couper un chemin existant.
35. Une mouche
ingénieuse
Rose prend cinq tuiles carrées dont chaque
côté mesure un mètre. Elle les dispose comme ci-après. Une mouche qui marche
sur la bordure de la figure devrait parcourir 10 mètres.
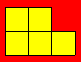
Agencez
autrement les cinq tuiles pour que la mouche parcoure 16 mètres sur la bordure,
tout en revenant à son point de départ.
36.
Sortie estivale
Un
certain nombre de jeunes se rendent au terrain de jeux L’Habitat. De ce
nombre, 11 jeunes portent un gilet rouge, 16 des espadrilles noires et 12 un
pantalon bleu. Parmi eux, cinq portent un gilet rouge et des espadrilles noires,
trois des espadrilles blanches et un pantalon bleu, deux un gilet rouge et un
pantalon bleu.
Combien y
a-t-il de jeunes qui se rendent à l’Habitat ?
37.
Rangées de trois
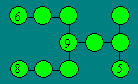
Placez
les nombres 1, 2, 4, 7, 8, 10 et 13 dans les cercles. La somme doit être égale
à 20 dans chaque rangée de trois cercles. Quatre nombres sont déjà en bonne
position.
38. Vers la maison
Partagez la grille en sept parties de même forme et de même
grandeur. Chaque partie doit contenir une maison et une bicyclette. Les cases
cadenassées sont exclues.
|
|
|
H |
|
H |
|
|
b |
Ï |
|
b |
H |
|
|
|
b |
H |
|
H |
b |
|
|
H |
|
b |
|
|
|
H |
|
b |
|
b |
Ï |
39.
Route de l’écureuil
Un écureuil se
déplace sur une charpente divisée en 16 petits carrés comme ci-après. Chaque
côté d’un petit carré mesure un mètre. L’écureuil part du coin de la
charpente où apparaît la toile d’araignée et se dirige vers la droite. Il
revient à son point de départ sans jamais passer plus d’une fois sur le
même côté.
Trouvez un
chemin où l’écureuil parcourt 22 mètres.
40.
Cure-dents en carrés
Jérémie a
disposé 24 cure-dents comme ceci.

Enlevez six
cure-dents pour obtenir cinq carrés.
41.
Dominos de Jade
Dans sa boîte de
dominos, Jade prend les sept pièces suivantes : (0, 5), (1, 1), (1, 2),
(1, 4), (2, 2), (2, 6) et (4, 5).
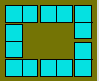
Placez les
dominos afin de pouvoir compter 10 points sur chacun des quatre côtés de ce
rectangle.
42. Les quatre
Claire
Dans l’addition suivante, chaque lettre de
Claire correspond à un chiffre différent.
|
C L A I R E
C L A I R E
+ C L A I R E
C L A I R E
E 1 5 3 8 4 |
Quel est le
mot qui correspond à E15384 ?
43.
Solitaire de Mégane
Mégane veut
atteindre le trésor caché dans la case 20. Elle doit partir de la case 1 et
suivre les indications données dans les cases qu’elle visite.
|
1 Départ
Avance
de 4
|
2
Avance
de 1
|
3
Recule
de 1
|
4
Recule
de 2 ou avance de 2 |
|
5
Avance
de 2 ou de 3 |
6
Avance
de 8
|
7
Recule
de 3 ou avance de 2 |
8
Avance
de 2 ou de 4 |
|
9
Avance
de 1 ou de 4 |
10
Recule
de 2 ou avance de 2 |
11
Recule
de 1 ou avance de 4 |
12
Avance
de 4
|
|
13
Recule
de 2 ou de 3 |
14
Avance
de 2
|
15
Avance
de 4 ou de 5 |
16
Avance
de 2 ou de 3 |
|
17
Avance
de 2 ou recule de 3 |
18
Recule
de 6
|
19
Recule
de 5
|
20
TRÉSOR
|
Il y a un seul
chemin pour se rendre au trésor. Quel est-il ?
44. Au foyer
Quatre familles et quatre maisons sont
disposées ainsi.
Reliez chacune
des familles à trois maisons par des cordes sans que jamais deux cordes ne se
croisent.
45.
Macarons de Zacharie
Zacharie a une
collection de macarons. Émilie voudrait savoir combien il en possède. Zacharie
lui dit : - Encercle deux à deux tout nombre et son double, comme 60 et
120. À la fin, additionne les nombres qui restent. Ce résultat t’indiquera
combien je possède de macarons.
|
50 |
82 |
80 |
51 |
90 |
60 |
|
160 |
182 |
72 |
101 |
140 |
61 |
|
210 |
100 |
122 |
105 |
83 |
81 |
|
162 |
120 |
200 |
100 |
142 |
107 |
|
202 |
164 |
70 |
166 |
103 |
91 |
|
102 |
206 |
180 |
71 |
92 |
214 |
Combien
Zacharie a-t-il de macarons ?
46.
Comme un ordinateur
Partez de la case
marquée DÉBUT. Suivez le sens des flèches et faites les opérations
indiquées. Quand vous atteignez un rectangle jaune, répondez à la question et
choisissez une des deux voies selon la réponse. À la fin, vous trouverez un
nombre.
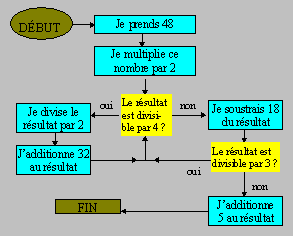
Quel est ce
nombre ?
47.
Numéros perdus
Six casiers sont
disposés comme ci-après. Trois casiers ont leur numéro ; les autres les
ont perdus. Au départ, les numéros avaient été attribués de telle manière
que chaque numéro est la somme des numéros des deux casiers inférieurs.
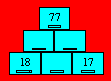
Retrouvez les
trois numéros qui manquent.
48.
Cure-dents en carrés
Alexia a disposé
24 cure-dents comme ceci :

Enlevez quatre
cure-dents pour obtenir cinq carrés.
49.
Nez à nez
Pascal, Fred, Lise
et David ont participé à une course de vitesse. Chacun des enfants a un nez de
type différent : pointu, camus, aquilin et retroussé.
1.
L’enfant qui a terminé au quatrième rang a le nez aquilin.
2.
Le nez de David n’est ni pointu ni aquilin.
3.
L’enfant au nez camus a obtenu le deuxième rang.
4.
Lise n’a pu se classer ni au premier ni au deuxième rang.
5.
Le nez de Lise n’est ni aquilin ni camus.
6.
Fred a un nez retroussé ou pointu.
7.
L’enfant qui a terminé au troisième rang a le nez pointu.
Trouvez le type de
nez de chaque enfant et leur rang dans la course.
50. En croissance
Chloé place un pion sur la case 10. Le pion
peut être déplacé horizontalement et verticalement, jamais en diagonale. Il
doit toujours atteindre une case dont le numéro est plus grand que celle qu’il
a quittée. Par exemple, le pion pourrait franchir les cases 10, 16, 21 et 42.
|
10 |
13 |
26 |
15 |
30 |
31 |
29 |
|
16 |
15 |
24 |
23 |
24 |
25 |
28 |
|
21 |
17 |
18 |
21 |
35 |
27 |
31 |
|
42 |
43 |
44 |
45 |
32 |
29 |
34 |
|
41 |
39 |
37 |
35 |
34 |
36 |
33 |
|
43 |
40 |
31 |
29 |
33 |
31 |
29 |
|
46 |
42 |
43 |
45 |
47 |
48 |
50 |
Trouvez un
chemin qui mène de la case 10 à la case 50. |
![]()
![]()