Ceci est le quatrième livre édité par Récréomath.

Débrouilleries
150 problèmes mathématiques et logiques

Les problèmes de ce livre ont été publiés dans le magazine Les Débrouillards de 1990 à 1996. Ce magazine drôlement scientifique s’adresse aux jeunes et à leurs parents.

Solutions 1 à 50

Solutions 101 à 150

*****************
Problèmes 101 à 150
*****************

Amélia s'amuse à écrire les chiffres dans une grille en plaçant une lettre par case. Aucun autre mot ou groupement de lettres ne doivent apparaître. Amélia a réussi à y inscrire les chiffres de TROIS à NEUF dans une grille 7 ´ 7.

Écrivez les mêmes chiffres dans une grille 6 ´ 9.

Remplissez cette grille en plaçant un chiffre par case.

A. J’ai un 6, un 7 et un 9. – Je suis le double de 19, 24 ou 29.

B. J’ai un 2, un 3, un 5 et un 9. – Je suis impair.

C. J’ai deux 2, un 4, un 7 et un 8.

D. Je suis impair. – J’ai deux 3, un 5 et un 8.

E. Je suis le triple de 17, 21 ou 24. – La somme de mes chiffres est 9.

F. J’ai un 2, un 7 et un 8. – La somme de mes chiffres est 11.

G. La somme de mes chiffres est 14. – J’ai un 5, un 6 et un 7.

H. J’ai deux 7 et un 9. – La somme de mes chiffres est 11.

I. J’ai deux 2, un 3 et un 6. – Je suis pair.

J. J’ai un 3, deux 4 et un 5.

K Je suis pair. – J’ai un 3, un 5 et deux 8.

L. J’ai un 2, un 3 et deux 8. – Je suis impair.

Félix dessine quatre figures géométriques avec une couleur différente et un numéro différent.

Figures : cercle, carré, triangle, losange

Couleurs : vert, bleu, jaune, rouge

Numéros : 3, 4, 7, 8

1. Le cercle n'est ni vert, ni jaune ; son numéro est supérieur de 1 à celui du carré.

2. La figure verte a un 4 et n'est pas le carré.

3. La figure qui a un 7 n'est pas le losange et n'est pas jaune.

4. La somme des numéros du triangle et de la figure jaune correspond au numéro de la figure bleue.

5. Le losange n'est pas vert ; son numéro est inférieur de 1 à celui du triangle.

Trouvez la couleur et le numéro de chacune des quatre figures.

104. Code d’Isabelle
Isabelle a inventé un code pour que personne ne puisse lire ses messages secrets. Elle fait correspondre une lettre à une autre. Ainsi, si Z est mis pour L, si B est mis pour U et si F est mis pour C, LUC s'écrira ZBF. Isabelle écrit les quatre mots suivants ; puis, elle place à droite les lettres correspondantes, mais dans le désordre.

P A I X : C G J K

A R M E : H K L Q

M I N E : C H L V

T A X E : D G H K

Quel mot correspond à J Q C L H ?

Une marmotte appelée Maxelle a creusé sous terre un véritable palais de 12 pièces. Chaque pièce est identifiée par une lettre. Chaque jour, Maxelle visite toutes les pièces de son palais. Elle peut s’arrêter plus d’une fois dans chacune ; mais elle doit emprunter tous les couloirs une seule fois.

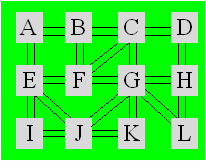
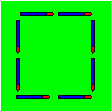
De quelle pièce devra partir Maxelle afin d’emprunter tous les couloirs ?

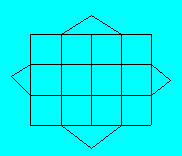
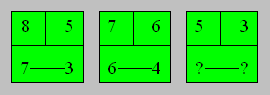
Hugo a écrit des chiffres dans quatre carrés.

Quel chiffre doit-on écrire à la place du point d’interrogation ?


107. Histoires de familles
Voici l’histoire de quatre familles. Pour chacune, trouvez le nombre d’enfants.

a) Martin a trois frères. Karine a deux sœurs. Martin est le frère de Karine.

b) Jean a trois sœurs. Claire a deux frères. Jean est le frère de Claire.

c) Serge a deux sœurs et un frère. Marie-Anne a deux frères et une sœur. Serge est le frère de Marie-Anne.

d) Rémi a deux frères et deux sœurs. Hugo a deux frères et deux sœurs. Hugo est le frère de Rémi.


108. Hexagones de Zoé
Zoé a écrit des nombres dans cette figure. Les nombres ont été formés en combinant les trois chiffres 5, 6 ou 7 de différentes façons par des opérations : +, –, ´ , ¸ . Par exemple, 2 = (5 + 7) ¸ 6, 72 = 65 + 7.

Zoé a fait deux erreurs de calculs si bien que deux nombres du tableau n’ont pas été formés de cette façon. Quels sont ces deux nombres ?

109. Vacances bien remplies

Pendant les vacances de Noël, Thomas, Laurence et Tristan ont été invités chez des amis : les Cormier, les Desrosiers et les Poirier. L’une des visites a duré trois jours, l’autre cinq et la troisième sept jours.

1. Thomas n’a pas visité les Cormier.

2. Laurence a eu un plus long séjour que Tristan.

3. Chez les Cormier, la visite a duré cinq jours.

4. Le séjour chez les Desrosiers a été plus long que celui chez les Poirier.

5. La visite de Thomas n’a pas duré sept jours.

Dans quelle famille, chacun est-il allé et quelle a été la durée du séjour ?

110. Sagesse de Maya

Maya a un peu plus de cinq ans. En fait, elle a vécu 1880 jours et elle connaît les chiffres. Son frère a rempli la grille avec des 1, des 8 et des 0. Il demande à Maya de lui dire combien de fois elle peut y lire 1880 en ligne droite. La lecture se fait en tout sens et même en diagonale.

Quel est ce nombre de fois ?


111. De cœur en cœur
Olivia a dessiné des cœurs et des étoiles comme ceci.

Tracez cinq lignes droites sans lever le crayon de façon à joindre tous les cœurs. Une ligne droite doit toucher à au moins trois cœurs. Il est permis de passer plus d’une fois sur un cœur.

112. Code secret

Pour entrer dans la caverne du Grand Galérien, il faut connaître le code secret.

Coloriez les nombres dont l’un est le triple de l’autre. Additionnez les nombres qui restent. La somme est le code secret. Quel est ce code ?


113. Nombres croisés
Remplissez cette grille en plaçant un chiffre par case.

A. J’ai un 2, un 3 et un 5. – Je suis le double de 41, 43 ou 49.

B. La somme de mes chiffres est 13. – J’ai un 5, un 6 et un 7.

C. J’ai deux 4, un 5, un 8 et un 9.

D. J’ai un 3, deux 5 et un 8. – Je suis un cube.

E. Je suis pair. – J’ai un 1, un 2 et un 4.

F. J’ai un 5, un 6 et un 9. – Je suis un cube.

G. Je suis le double de 13, 23 ou 33. – J’ai un 2 et deux 5.

H. J’ai deux 3, un 4 et un 7. – Je ne suis ni 5 ni 9.

I. Je suis impair. – J’ai un 1, un 5, un 8 et un 9.

J. J’ai un 4, deux 5 et un 9.

K Mes trois chiffres sont plus grands que 6. – J’ai un 2 et un 6.

L. J’ai un 4, un 6 et deux 8. – Je suis un carré.


114. On collectionne

Maxime a mis 12 timbres dans une enveloppe : cinq timbres de France, quatre d'Italie et trois du Canada. Il demande à Océane de piger au hasard dans l'enveloppe afin d'obtenir deux timbres d'un même pays.

Combien de timbres doit-elle piger pour être certaine d’obtenir deux timbres d'un même pays ?


115. Nombres brouillés
Remplissez cette grille en plaçant un chiffre par case. Les chiffres sont donnés horizontalement et verticalement, mais pas nécessairement dans le bon ordre.

116. Additions multiples
Dans le tableau, les nombres sont additionnés horizontalement et verticalement. Chaque figure représente un chiffre différent. Par exemple, n est mis pour 6 et ¨ pour 5. Deux ou trois figures accolées forment un nombre de deux ou trois chiffres.

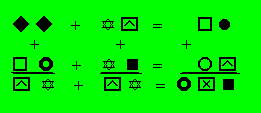
Trouvez la valeur de chaque figure.


117. En hauteur
Carole est plus petite que Nicolas.

Charlotte est plus grande que Félix.

Carole est plus grande que Catherine.

Nicolas est plus grand que Charlotte.

Carole est plus petite que Félix.

Placez les six personnes en ordre à partir du plus grand.


118. Fête champêtre
Lors d’une fête champêtre, Victor a compté 154 enfants dans les sept chalets du parc. Le chalet A contenait 27 enfants tandis que le B en contenait 16. Victor a remarqué qu’il y avait 66 enfants dans chaque rangée de trois chalets reliés par un sentier.

Combien y avait-il d’enfants dans les chalets autres que A et B ?


119. Courir, sauter, lancer
Marc, Sandra et Véronique se sont inscrits chacun à trois épreuves d'athlétisme. Chacun a participé à une épreuve dans chaque catégorie.

Courses : 100 m, 400 m, 1500 m

Sauts : longueur, hauteur, perche

Lancers : poids, disque, javelot.

1. Marc n'a pas sauté à la perche.

2. C'est Sandra ou Véronique qui a lancé le disque.

3. La personne qui a couru le 400 m a sauté en longueur.

4. Marc ou Véronique a gagné la course du 100 m.

5. La personne qui a lancé le poids a perdu au saut à la perche.

6. Ni Marc ni Sandra n'ont sauté en hauteur.

Trouvez à quelles épreuves les trois amis ont participé.

Aline a égaré son billet pour entrer au cinéma. Toutefois, elle sait que son numéro de billet est un des six suivants chacun diminué de 2 :

554639             392684             816692

834521             663584             745593

1. La somme des chiffres est 30.

2. Le numéro comporte deux chiffres identiques.

3. La somme des trois premiers chiffres est 15.

4. La somme des deux derniers chiffres est 10.

Trouvez le numéro du billet d'Aline.


121. Vive le chocolat !
Noémie, Justin, Philippe et Tristan ont visité une fabrique de chocolat. À leur départ, on leur a remis une immense tablette de chocolat taillée bizarrement comme ceci.

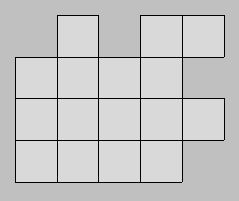
Partagez la tablette en quatre parties de manière à ce que tous les morceaux aient la même forme et la même grandeur.

122. Une différence

Chacun des numéros des boules du premier losange est supérieur d’un même nombre à un numéro du second losange.

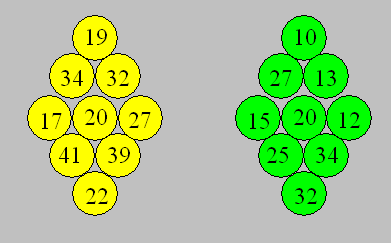
Quel est l’écart qui sépare les numéros d’un losange à l’autre ?

123. Des bâtons propres

Cette figure a été construite avec 24 bâtonnets. Elle contient quatre petits carrés. Ajoutez huit bâtonnets pour avoir neuf petits carrés en tout. Les bâtonnets que vous ajoutez peuvent être voisins seulement dans les coins.

124. Vrai ou faux ?

Line, Charlotte et Yves ont répondu à un examen comportant six questions de type vrai (V) ou faux (F). Voici les réponses données par chacun aux questions numérotées :

1. Chacun d’eux a réussi quatre questions.

2. Line a réussi la première question.

3. Yves a raté la troisième question.

4. Charlotte a réussi la cinquième question.

Trouvez les six bonnes réponses de l'examen.

Dans les cases du tableau suivant, Annabelle veut écrire neuf nombres : 6, 7, 8, 9, 10, 11, 12, 13 et 14.

Placez chaque nombre en respectant les indications données à gauche et en haut de la grille.

126. Un mini-tournoi

Jérémie, Catherine, Mégane et Simon ont participé à un mini-tournoi de ping-pong.

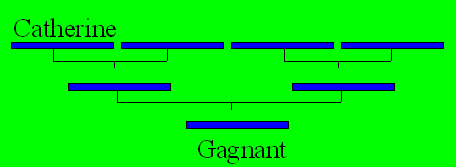
1. Catherine a gagné contre Simon.

2. Mégane a perdu contre Simon.

3. Jérémie a perdu contre Catherine.

Qui a gagné le tournoi ?

127. Glissements de jetons

Découpez huit jetons. Écrivez sur chaque jeton chacune des lettres de AMI, OS et BLE. Placez les jetons sur une grille carrée de neuf cases comme il est montré à gauche.

Déplacez les jetons en les faisant glisser de leur case à une case voisine vide. À la fin, vous devez obtenir la configuration de droite.


128. Une rencontre heureuse
Trois personnages célèbres discutent tranquillement. Chacun porte un macaron. De plus, l'un a une cravate bleue ; l'autre un foulard vert et le troisième une cravate grise.

1. Fermat est le plus volubile des trois.

2. Le macaron de Newton représente une pomme.

3. Pascal porte un macaron sur lequel apparaît une calculatrice.

4. Le moins volubile porte un foulard vert.

5. Celui dont le macaron représente une marguerite n'a pas de cravate bleue.

6. Pascal est à côté de celui qui porte une cravate bleue.

Qui porte la cravate grise ?


129. Le jeu des menteurs
Mathieu, Simon et Caroline sont assis dans un parc. Deux des enfants portent des espadrilles tandis que le troisième a chaussé des patins à roulettes.

Deux des enfants disent : - Je suis un garçon.

Le troisième dit : - Je suis une fille.

Un peu plus tard, Mathieu et Caroline disent chacun : - Je porte des espadrilles.

Simon déclare : - Je suis en patins à roulettes.

Il y a deux menteurs dans le groupe. Qui sont-ils ?


130. Lectures de Nadia
Pendant les vacances, Nadia a lu quatre romans : Assiettes vides, Pièges carnivores, Pleine Lune et Tendres passions.

Héros : Cambo, Ergo, Rhombum et Tantum

Héroïnes : Aquarina, Mélita, Nacella et Otita

1. Ergo n’est pas le héros d’Assiettes vides. Aquarina n’en est pas l’héroïne.

2. Dans Pièges carnivores, le héros n’est pas Rhombum ; l’héroïne n’est ni Mélita ni Otita.

3. Ergo se trouve dans le même roman qu’Otita.

4. Mélita et Cambo sont dans le même roman qui n’est pas Tendres passions.

5. Rhombum et Nacella ne sont pas dans Pleine lune et ne sont pas dans le même roman.

6. Nacella et Otita ne sont pas les héroïnes d’Assiettes vides.

Trouvez le nom du héros et de l’héroïne de chaque roman.


131. Nombres croisés
Remplissez cette grille en plaçant un chiffre par case.

A. Je suis un carré. – J’ai deux 3 et un 7.

B. La somme de mon premier et de mon dernier chiffre est égale à celui du milieu. – Je suis le triple de 17, 27 ou 37.

C. Je suis un chiffre pair. – J’ai un 4 et trois 9.

D. J’ai deux 4 et deux 7.

E. La somme de mes chiffres est 19. – Je suis la moitié de 10 ou de 12.

F. Je suis le double de 30, 32 ou 34. – J’ai un 4 et deux 6.

G. Je suis le quadruple de 106, 126 ou 146. – La somme de mes chiffres est 8.

H. J’ai deux chiffres identiques. – J’ai un 2, un 4 et un 7.

I. J’ai deux 7 et deux 9.

J. Mon triple est un carré. – J’ai deux 4 et deux 6.

K. La somme de mes chiffres est 28. – Je suis plus grand que 4.

L. J’ai un 1, un 3 et un 9. – La somme de mes chiffres est 9.


132. Un casse-tête géométrique
La figure suivante est composée d’un rectangle, de quatre triangles égaux et de trois carrés.

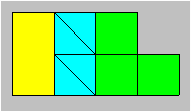
Découpez les huit pièces. Agencez-les pour former un octogone.


133. Tour de Lucette
Luc a additionné quatre nombres de quatre chiffres dont la somme est 11 405. Lucette lui a joué un tour et a effacé deux nombres. Lucette dit à Luc :
- Je peux t'aider à retrouver ces deux nombres. L'un des nombres effacés est supérieur de 23 à l'autre.

Trouvez les deux nombres qui manquent.


134. Carrés d’Olivia
Olivia a rempli les trois premiers carrés.

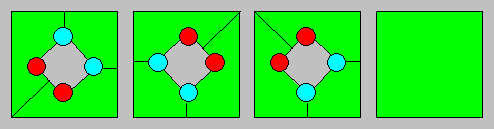
En vous basant sur les trois premiers dessins, complétez le quatrième carré.


135. Un casse-tête géométrique
Le rectangle suivant a d’abord été divisé en deux carrés de même grandeur. Dans le premier, on y trouve dans les coins quatre triangles égaux et au centre deux triangles égaux. Le deuxième carré est subdivisé en un rectangle et deux carrés égaux qui occupent le même espace que le rectangle.

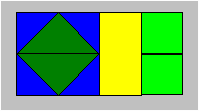
Découpez les neuf pièces. Agencez-les pour former un rectangle dans lequel seul un carré vert touche au rectangle jaune.


136. Lettres de Pierre
Pierre écrit : A + B + C = 12 et D + E + F = 12. Il donne à chaque lettre une valeur différente de 1 à 7, sauf 4. 

Attribuez une valeur à chaque lettre pour que A² + B² + C² = D² + E² + F².


137. Allumettes de Noémie
Noémie dispose huit allumettes pour former un carré.

Déplacez quatre allumettes pour construire un carré et deux triangles.


138. Tuiles d’Yvan
Yvan a assemblé des tuiles carrées pour obtenir cette figure (partie verte).

Partagez cette figure en quatre parties de même forme et de même grandeur.


139. Addition de Thomas
Thomas a écrit l’addition suivante dans laquelle chaque lettre représente un chiffre différent. Les chiffres sont : 1, 2, 4 et 6.

Quelle est la valeur de VPR ?


140. Tout d’un trait
Camillia veut reproduire cette figure d’un trait continu, soit sans lever le crayon.

De quel point devra-t-elle partir ?


141. En manque
Trouvez le nombre qui devrait remplacer les points d’interrogation.

142. Boules d’Alex
Alex a écrit les 10 chiffres à l’aide de boules et de segments de droite. Par exemple, il faut 12 boules pour écrire 80.

Trouvez le plus grand nombre qui contient
a) 11 boules

b) 12 boules

c) 13 boules


143. D’un à quatre
Une mouche part du premier 1 de la ligne supérieure. Elle passe par cette suite : 1, 2, 3, 4, 1, 2, 3, ... horizontalement ou verticalement, mais jamais en diagonale.

Trouvez le chemin qui s’arrête au premier 4 de la ligne inférieure.


144. Agathe et son torpilleur
Agathe recouvre quatre petits carrés par un T comme dans l’exemple. Elle appelle le T un torpilleur. Pour que le torpilleur n’explose pas, il faut que la somme des quatre nombres couverts soit 15.

Placez six autres torpilleurs qui n’exploseront pas.


145. Cure-dents en carrés
Émile a disposé 24 cure-dents comme ceci :

Enlevez huit cure-dents pour obtenir cinq carrés.


146. Pot-pourri

a) Quel est le quart de quatre multiplié par 4 ?

b) Quel est le dixième de 50 au carré ?

c) Quel est la moitié du quart du triple de 24 ?


147. Le T de Tommy

Tommy trace un T tel que la barre transversale a les mêmes mesures que le pied. Par la suite, il trace deux droites parallèles. Il découpe le T en suivant les lignes ajoutées. Il obtient ainsi quatre pièces.

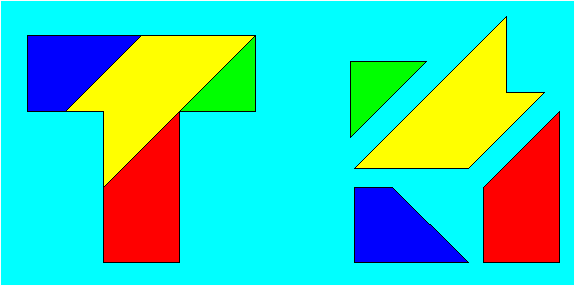
Préparez les pièces et reconstituez le T.

148. Nombres croisés

Remplissez cette grille en plaçant un chiffre par case.

A. J’ai un 4, un 5, un 7 et un 8. – Je suis impair.

B. Je suis le triple de 13, 16 ou 26. – J’ai un 2, un 5 et un 8.

C. J’ai un 2 et deux 8. – La somme de mes chiffres est 13.

D. Je suis impair. – J’ai deux 5 et un 6.

E. Mes chiffres sont 3, 4, 5, 6 et 7.

F. J’ai un 4, un 6 et deux 7. – Je suis pair.

G. J’ai deux 3, un 7 et un 8. – Je suis un carré.

H. J’ai deux 8 et un 9. – J’ai deux chiffres identiques.

I. Je suis impair. – J’ai un 2, deux 5 et un 6.

J. La somme de mes chiffres est 9. – J’ai deux 6 et un 7.

K. La somme de mes chiffres est 24.

L. J’ai un 2 et deux 5. – J’ai deux chiffres identiques.


149. Abeille voyageuse
Une abeille part de la cellule 30. Elle avance sur une cellule voisine seulement si le numéro de celle-ci est supérieur de 4 ou inférieur de 3 au numéro de la dernière cellule atteinte. De cette façon, l’abeille doit visiter toutes les cellules.

Sur quelle cellule l’abeille terminera-t-elle son voyage ?


150. Cavalier de Laurie
En partant de la case numéro 1, Laurie déplace le cavalier. Ce dernier doit passer une seule fois dans chaque case jusqu’à ce qu’il ait atteint toutes les cases. Les 16 premiers sauts sont indiqués.

Numérotez au passage chaque case de 17 à 49.

Solutions 1 à 50

Solutions 101 à 150