|
| |
|

|
Publications |
|
Ceci est le cinquième livre édité par Récréomath.
Évasions calculées
80 problèmes mathématiques et logiques
Par Charles-É. Jean
|
|
Les problèmes de ce livre ont été publiés
par Modulo Éditeur en 1982. Quelques modifications mineures ont été apportées au
texte notamment pour satisfaire la mise en page.
|
***************
Problèmes
1 à 40
***************
|
1.
Évasion … calculée
C’est le 25 avril, Denis écoute
attentivement le juge qui semble lui formuler une curieuse sentence.
- Voilà 10 clés, dit le juge. Chaque clé permet d’ouvrir l’une des 10
portes consécutives qu’il faut franchir pour sortir de la prison. Chaque
jour, à partir de demain, tu pourras introduire une clé par porte et franchir
plus d’une porte. À chaque réussite, tu auras le droit de marquer les
clés et de faire un nouvel essai la journée même ; mais à chaque
échec, tu devras attendre au lendemain. Quand tu reviendras dans ta cellule,
les portes se refermeront à clé automatiquement.
Denis est fort heureux de sa sentence. Il se dit qu’avec un
peu de chance, il pourra quitter sa geôle dans quelques jours. Toutefois, Denis
fut très malchanceux. C’est au 10e jour seulement qu’il réussit
à ouvrir la première porte. De même, pour chacune des autres portes, il dut
essayer toutes les clés avec lesquelles il n’avait pas encore réussi à
ouvrir de portes.
À quelle date, Denis réussit-il son évasion…
calculée ?
|
|
|
2. La collection de Serge
De sa collection, Serge retire 11 timbres dont la valeur individuelle
varie de 5 ¢ à 15 ¢.
Après avoir placé les timbres de 5 ¢, de 7 ¢ et de 9 ¢
comme ci-après, il désire disposer les autres de façon à ce que la valeur
totale soit de 32 ¢ sur chaque rangée de trois timbres reliés par une droite.
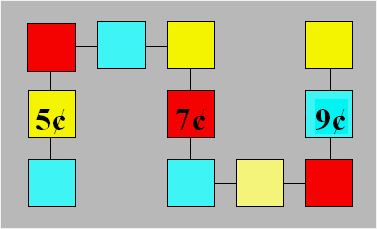
Quelle sera la disposition finale ?
|
|
|
3. Des postes de péage
Quatre villes sont reliées par le réseau routier ci-contre. Il y a
un poste de péage dès qu’au moins deux routes se croisent. L’automobiliste
qui emprunte une route dessinée verticalement ou horizontalement doit
débourser 0,75 $ au poste de péage ; par contre, celui qui emprunte une
route diagonale doit verser 1,05 $.
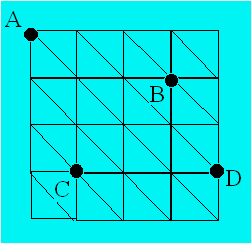
Réginald part de A. Il doit passer par B et par C, pas nécessairement dans
l’ordre, pour terminer son voyage à D, immédiatement après le poste de
péage.
Quel est le montant minimal que Réginald doit débourser
pour son voyage ?
|
|
|
4. Trudeau, Lévesque et la Constitution
Depuis longtemps, les problèmes de traversées passionnent
bien des gens. Le premier problème connu est dû à Abbott Alcuin
(735-804), un des principaux collaborateurs de Charlemagne. C’est l’histoire
du loup, de la chèvre et des choux. En voici une variante :
Par un curieux hasard que seuls les politiciens
peuvent comprendre, Pierre Trudeau et René Lévesque se trouvaient sur
une île avec la Constitution. Lorsqu’ils voulurent revenir sur la
terre ferme, ils ne trouvèrent qu’un seul bateau disponible.
Le batelier méfiant refusa de faire traverser en
même temps les deux hommes et le document. Il acceptait de les
accueillir dans son bateau mais séparément. De plus, soupçonnant
quelques problèmes, il ne voulait pas laisser Trudeau seul avec
Lévesque, ni laisser Lévesque seul avec la Constitution.
Comment devra-t-il procéder pour ramener les deux
hommes et la Constitution sur la terre ferme ?
|
|
|
5. Une famille de quatre enfants
Germain dit : - Je suis l’aîné.
Germain ment deux fois sur cinq.
Sandra dit : - Je suis la deuxième.
Sandra dit la vérité deux fois sur trois.
Michel dit : - Je suis le troisième.
Michel ment une fois sur quatre.
Louise dit : - Je suis la cadette.
Louise dit la vérité deux fois sur cinq.
Parmi les quatre enfants, les deux qui disent plus
souvent la vérité font une affirmation vraie tandis que les deux
autres mentent.
Dans quel ordre, les enfants de cette famille
sont-ils nés ?
|
|
|
6. Un réseau routier
Huit villes sont reliées entre elles par le réseau routier
ci-dessous.
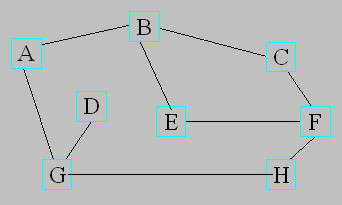
Valin part de A pour se rendre à D. Il doit
parcourir le réseau en entier et ne jamais utiliser la même route deux
fois de suite. Valin a besoin d’une journée pour parcourir la
distance entre deux villes et s’arrête pour la nuit à chaque
endroit.
En combien de jours, au minimum, pourra-t-il
effectuer son voyage ?
|
|
|
7. Curiosités numériques
Les chiffres rebondissent parfois avec régularité. Dans
chacun des cas, effectuez les quatre premières opérations en utilisant
de préférence votre calculatrice.
|
77 ´ 77 = |
|
777 ´ 77 = |
|
7777 ´ 77 = |
|
77 777 ´ 77 = |
|
777 777 ´ 77 = |
|
12 ´ 99 = |
|
123 ´ 99 = |
|
1234 ´ 99 = |
|
12 345 ´ 99 = |
|
123 456 ´ 99 = |
Par la suite, vous tenterez de deviner le dernier
résultat en comparant les résultats trouvés.
|
|
|
8. Des cartes magiques
Les cartes à jouer constituent, sans aucun doute, le jeu le
plus connu et le plus populaire. De nombreuses heures sont consacrées
à ce divertissement dont les variantes vont de la haute stratégie (au
bridge) au pur hasard (à la bataille). Même les enfants trouvent du
plaisir à ériger des châteaux de cartes ou à réaliser d’autres
constructions fantaisistes.
Lorsque les cartes apparurent en Europe, au XVe
siècle, elles se répandirent rapidement malgré les difficultés de
communication d’alors. Saint-Bernard de Sienne, outré par le fait que
les gens y jouaient beaucoup, déclara que le diable était à l’origine
de cette invention. Il interdit aux gens de s’y adonner, sinon ils se
retrouveraient en enfer avec leurs cartes. À Paris et à Rome, des
magistrats et des prêtres brûlèrent des cartes sur la place publique.
Malgré ces interdictions, le jeu de cartes a traversé les siècles.
Sortez donc votre jeu de cartes et retirez les neuf
cartes ci-contre :
|
2 © |
4 © |
6 © |
|
3 § |
5 § |
7 § |
|
4 ¨ |
6 ¨ |
8 ¨ |
Disposez vos neuf cartes en trois rangées de trois
de telle sorte que les valeurs totalisent 15 dans chaque rangée
horizontale, dans chaque rangée verticale et dans chacune des deux
diagonales principales. De plus, on doit retrouver du cœur, du carreau
et du trèfle dans chaque rangée horizontale et dans chaque rangée
verticale.
|
|
|
9. Deux familles de trois enfants
Trois parents disent chacun trois phrases dont la première
est vraie et les deux dernières sont fausses.
Louise : Je suis la soeur de
Pierre.
Robin est mon fils.
Pierre est le père de Serge.
Pierre : Je suis le père de
Marlène.
Olivier est mon fils.
Annie est la mère de Serge.
Claude : Je suis l’oncle de
Natacha.
Didier est le cousin de
Serge.
Annie est la fille de Robin.
Nommez les deux parents et les trois enfants de
chacune des deux familles.
|
|
|
10. Une traversée
Deux voyageurs arrivent sur le bord d’une rivière. Comme
ci-contre, des
roches sont disposées dans la rivière de telle sorte que la distance
entre deux roches voisines soit toujours la même tant horizontalement
que verticalement.
|
Å |
Å |
|
Å |
Å |
|
Å |
|
Å |
Å |
|
|
|
Å |
Å |
Å |
Å |
|
|
Å |
Å |
Å |
|
Les voyageurs peuvent mettre le pied sur une roche à
la condition que l’espace enjambé soit toujours de la même longueur
sur tout le trajet. De plus, chacun doit utiliser six roches que l’autre
n’utilise pas et aucun des deux ne peut revenir en arrière.
Déterminez un chemin qui permettra à chacun de
traverser la rivière.
|
|
|
11. Un certain quantième
Monique et Ginette sont en train d’examiner le mois d’avril
sur un calendrier. Ginette s’exclame alors : - J’ai hâte que
le jour de mon anniversaire de naissance arrive.
|
D |
L |
M |
M |
J |
V |
S |
| |
|
|
|
1 |
2 |
3 |
|
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
11 |
12 |
13 |
14 |
15 |
16 |
17 |
|
18 |
19 |
20 |
21 |
22 |
23 |
24 |
|
25 |
26 |
27 |
28 |
29 |
30 |
|
Monique
reprend : - Quel quantième est-ce ?
Ginette explique : - La
somme des huit nombres qui touchent à ce quantième est 168.
À quel quantième d’avril arrive l’anniversaire
de naissance de Ginette ?
|
|
|
12. Les cachettes de Sandra
Sandra voulut jouer un tour à Stéphane. Elle dessina
différents carrés qui représentaient des chiffres et lui montra l’addition
suivante :
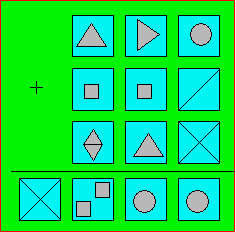
- Tu dois
reconstituer l’addition, annonça Sandra.
Stéphane
reprit : - J’en suis incapable. Il y a trop de carrés
différents.
- Ça
va ! Je te donne quatre indices, répondit Sandra.

Reconstituez l’addition.
|
|
|
13. Jeu de monnaie
Deux amis, Michel et Pierrette, ont chacun quatre pièces de
monnaie.
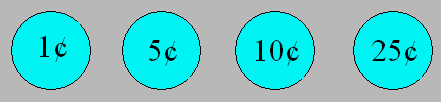
En même temps, chacun montre à l’autre une des
pièces. Si la somme des deux pièces donne un nombre pair, Pierrette
gagne un dollar à même une mise commune de 80 dollars. Si cette somme
est impaire, c’est Michel qui gagne un dollar. Les deux amis
conviennent de toujours choisir la pièce au hasard.
Comment sera partagé le montant de 80 dollars, selon
toute probabilité ?
|
|
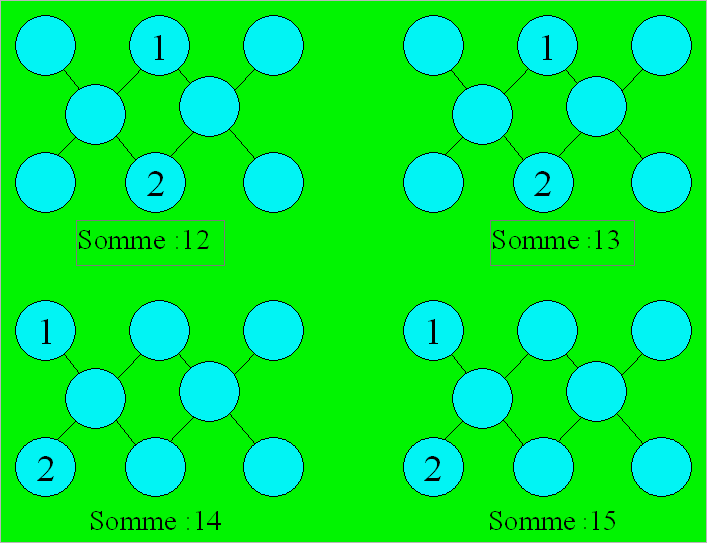
14.
Le khi magique
Disposez les nombres de 3 à 8, pris
chacun une seule fois, dans chacune des quatre figures ci-contre. La
somme des nombres de chaque rangée de trois cercles alignés est
indiquée en bas de chaque figure.
|
|
|
15. Au fil des ans
Elles sont cinq amies :
Marthe, Brigitte, Sonia, Gisèle, Patricia. Écoutons la conversation de
trois d’entre elles.
Brigitte :
- Je suis plus jeune que Sonia et plus âgée que Patricia.
Marthe :
- Je suis plus jeune que Gisèle et plus âgée que Patricia.
Sonia :
- Je suis plus jeune que Gisèle et plus âgée que Marthe.
Qui est la plus âgée parmi les cinq amies ?
|
|
|
16. Le roi aux échecs
Guy est un joueur d’échecs très méthodique. Il place son
roi dans un coin de l’échiquier sur la case marquée A. Il avance le
roi d’un rang vers le camp opposé par case consécutive, et ce,
uniquement sur les cases marquées d’un point.
|
A |
|
|
|
|
|
|
|
|
|
· |
|
|
|
|
|
|
|
· |
|
· |
|
|
|
|
|
|
|
· |
|
· |
|
|
|
|
|
· |
|
· |
|
· |
|
|
|
|
|
· |
|
· |
|
· |
|
|
|
· |
|
· |
|
· |
|
· |
|
|
|
· |
|
· |
|
· |
|
· |
Combien y a-t-il de chemins possibles pour se rendre
sur les quatre cases à l’autre extrémité de l’échiquier, sans
jamais revenir en arrière ?
|
|
|
17. Combinaisons de nombres
Au moyen d’opérations, on peut combiner des nombres et
obtenir différents résultats. Dans le cas présent, utilisez deux 2 et
deux 3. Vous pouvez vous servir des opérations suivantes : l’addition,
la soustraction, la multiplication, la division ou l’élévation à
une puissance. Exemple : 48 = 23 ´
2 ´ 3 et 28 = (3 + 2)2 + 3.
|
10 |
|
55 |
|
|
12 |
|
64 |
|
|
13 |
|
108 |
|
|
17 |
|
166 |
|
Représentez les nombres du tableau suivant.
|
|
|
18. Le dé de Nicolas
Nicolas a mis au point un dé tout à fait original : un
dé à cinq faces. Je lui ai demandé de m’en fournir le dessin.
Malheureusement, il a refusé de me montrer les cinq faces numérotées
1, 2, 3, 4 et 5. Toutefois, il m’a assuré qu’en lançant le dé au
hasard, celui-ci avait autant de chances de tomber sur l’une
quelconque de ses cinq faces. Il a ajouté :
- J’aimerais jouer une partie de dés avec toi.
Chacun notre tour, nous lancerions deux dés à cinq faces. Si la somme
des points était 4, 5, 6 ou 7, tu me donnerais un dollar et si la somme
était 2, 3, 8, 9 ou 10, je te donnerais un dollar. Comme tu as pour toi
cinq sommes et moi quatre, tu es certain de gagner plus d’argent que
moi.
J’accepte le marché. Mais après avoir lancé le
dé une centaine de fois, j’avais perdu 30 dollars.
Ai-je été malchanceux ou berné par Nicolas ?
|
|
|
19. Une héroïne
En 1692, Madeleine de Verchères, alors âgée
seulement de 14 ans, repoussa avec courage une attaque contre le manoir
familial. La légende raconte qu’elle mystifia ses assaillants en
multipliant les apparitions dans les différentes fenêtres.
La description de la façade du manoir et les
quelques détails (!) que j’ai trouvés ici et là m’ont amené à
formuler une interprétation. En effet, sur trois étages il y avait
huit fenêtres disposées comme dans l’illustration. Au centre, il y
avait un balcon tellement proéminent que les assaillants, selon leur
position, ne pouvaient voir qu’une rangée de trois fenêtres à la
fois.
Dans un premier temps, Madeleine de Verchères
disposa ses 36 soldats de façon à ce qu’il y en ait un à chaque
fenêtre de coin et huit à chaque autre fenêtre ; les assaillants
comptaient ainsi 10 soldats par rangée.
Lors de la première attaque, Madeleine perdit quatre
soldats. Mais pour tromper les assaillants, elle montra 11 soldats à
chaque rangée.
Une deuxième attaque eut lieu où elle perdit encore
quatre soldats. Toutefois, elle en fit voir alors 12 par rangée. Voyant
cela, les assaillants prirent la fuite.
Comment, après chaque attaque, Madeleine de
Verchères disposa-t-elle ses soldats pour réussir ce
stratagème ?
|
|
|
20. Un plancher d’immeuble
Le diagramme ci-contre représente le plancher d’un
immeuble où on trouve 19 chambres communiquant entre elles. Sept portes
extérieures permettent en plus de pénétrer dans l’immeuble.
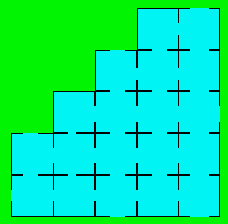
Le gardien de sécurité doit chaque jour inspecter l’immeuble
en passant une seule fois au milieu de chacune des chambres. Il doit le
plus possible faire un virage à l’intérieur de chaque chambre. Le
gardien entre dans l’immeuble au début de son inspection et en
ressort à la fin.
Tracez le chemin suivi par le gardien.
21. Billard électronique
- Prends le triangle, lui dit
Rachelle, et place les boules sur la table. Nous allons commencer à
jouer.

-
As-tu remarqué, reprit Jean-Yves, comment les boules sont
disposées ?
-
Il y a longtemps que j’ai remarqué qu’il y a cinq boules à la
base, puis une de moins sur chaque rangée horizontale, de la base au
sommet.
-
S’il y avait 100 boules à la base, combien, selon toi, y aurait-il de
boules en tout ?
-
C’est facile de faire la somme. Mais je vais essayer de trouver une
méthode plus rapide.
-
Pendant que tu cherches, moi je compose un programme pour l’ordinateur
afin de déterminer la quantité totale de boules lorsque la base varie
de deux à 100 boules.
Combien y a-t-il de boules en
tout lorsqu’il y en a 100 à la base ?
22.
Qui est propriétaire ?
1. Danielle n’a pas 35 ans et elle n’est pas propriétaire de la
parfumerie.
2.
Laurette n’a pas 34 ans et elle n’est pas propriétaire de la
boutique d’art.
3.
Francine n’a pas 29 ans et elle n’est pas propriétaire du
dépanneur.
4.
La propriétaire du dépanneur n’a pas 35 ans.
5.
La propriétaire de la parfumerie n’aime pas Laurette.
6.
Les trois femmes ont respectivement 29, 34 et 35 ans.
Désignez la propriétaire de
chaque commerce et déterminez son âge.
|
Nom |
Âge |
Commerce |
|
Danielle |
|
|
|
Laurette |
|
|
|
Francine |
|
|
23. Le cavalier
Le cavalier aux échecs se
déplace en L. Si on exclut la case de départ, il parcourt deux cases
à gauche ou à droite et une case en haut ou en bas ; ou encore il
parcourt deux cases en haut ou en bas et une case à gauche ou à
droite.
Dans chacune des quatre grilles,
en partant de la case numéro 1, déplacez le cavalier de telle sorte qu’il
passe au plus une fois sur chaque case et jusqu’à ce qu’il ait
atteint le maximum de cases. Pour faciliter le jeu, numérotez au
passage chaque case.
Dans chacun des cas, quel est le
maximum de cases atteintes ?
24. Deux coureurs
Une piste de course circulaire
mesure 13 kilomètres. Yves a parcouru 342 kilomètres à partir du
point de départ. De son côté, Mia a parcouru 226 kilomètres toujours
à partir du point de départ.
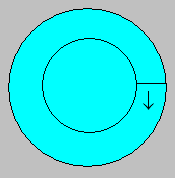
Lequel des deux coureurs a
parcouru une plus grande distance dans son dernier tour ?
25. Dollard au Long-Sault
Lorsqu’en 1660 Dollard
des Ormeaux eut conçu le projet de défendre la colonie et que son
projet s’ébruita dans la population de Ville-Marie, 36 jeunes gens se
présentèrent à lui pour faire partie de l’expédition. Dans son for
intérieur, Dollard décida de ne retenir que 16 candidats, en
particulier à cause d’un partage éventuel des ballots de fourrure.

Afin de ne décevoir personne à
cause de son choix, Dollard fit placer les 36 jeunes gens en cercle. Il
compta de 5 en 5 et élimina chaque fois le 5e, et ce, jusqu’à
ce qu’il en reste 16. Dans le groupe, Dollard avait six amis. Ils se
placèrent respectivement aux 6e, 12e, 18e,
24e, 30e et 36e rangs, par rapport à l’endroit
où Dollard commença à compter.
Combien de ses amis ont-ils
été choisis ?
26. Les billes de Simon
Simon possède 70 billes. Il doit
placer ses billes dans sept sections d’un coffre ayant la forme
suivante :
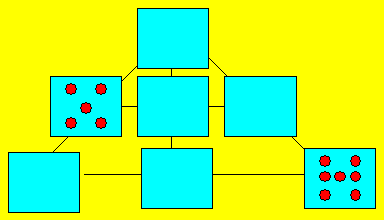
Le nombre de billes doit être
de 30 dans chacune des cinq rangées de trois sections. Par ailleurs,
deux sections du coffre contiennent chacune cinq et sept billes.
Combien Simon placera-t-il de
billes dans les autres sections ?
27. Deux pommes
Voilà ce que Marcel a écrit
dans son cahier. Il était loin de se douter que sa voisine Christiane y
avait vu une énigme.
UNE
pomme + UNE pomme = DEUX pommes
En effet, elle se demandait si
en remplaçant chaque lettre par un chiffre de 1 à 8, on pourrait
réaliser l’addition ci-dessous.
Elle se mit à l’œuvre et
elle finit par trouver pour chaque lettre un chiffre de 1 à 8 qui
rendait l’addition vraie.
Reconstituez l’addition.
28.
Les règlements d’Isabelle et d’Alain
Isabelle et Alain ont inventé un
nouveau jeu de dés.
-
Voilà, dit Isabelle, je lance les deux dés en même temps. Si j’obtiens
deux dés identiques, je te donne 5 $. Sinon, tu me donnes
3 $.
-
Quant à moi, reprend Alain, si j’obtiens une somme plus grande que 8,
je te donne 3 $. Sinon, tu me donnes 5 $.
Après avoir lancé les dés
chacun 18 fois, combien, selon toute probabilité, chacun aura-t-il
gagné ?
29. Face contre table
Huit cartes sont placées face
contre table comme ci-dessous.
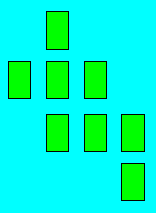
1.
Le valet de cœur est au-dessous du 9 de carreau dans la même rangée
verticale mais ne lui est pas voisin.
2.
Le valet de trèfle est immédiatement à gauche du 10 de cœur dans la
même rangée horizontale.
3.
Le 9 de pique est immédiatement au-dessus du 10 de carreau dans la
même rangée verticale.
4.
Le 9 de trèfle est immédiatement au-dessous du valet de carreau dans
la même rangée verticale.
5.
Le 10 de carreau est au milieu d’une rangée horizontale.
Déterminez la position de
chaque carte.
30. Des cercles en losange
Placez dans les cercles des
nombres impairs de façon à ce que la somme des cercles reliés par une
même droite soit toujours 27 dans le premier losange et 64 dans le
second. Des nombres sont déjà inscrits dans chaque figure. Les autres
nombres à placer sont donnés en bas.
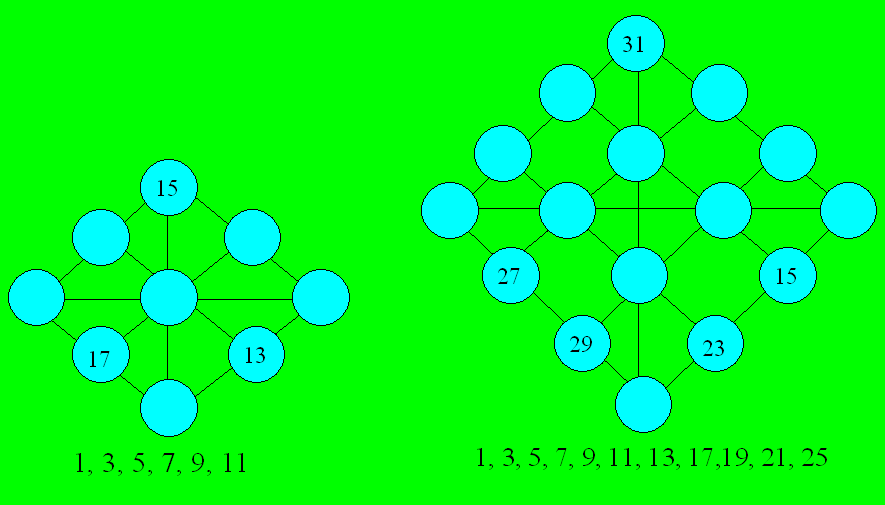
31. Domino Gratias
Les dominos sont connus depuis fort
longtemps. Les anciens Grecs, les Hébreux et les Chinois y ont joué bien
avant nous selon des règles particulières. Plus près, c’est en 1791
que ce jeu fut introduit en France. Les moines des couvents d’Italie l’avaient
d’ailleurs adopté et le gagnant s’exclamait Domino Gratias (Grâces
soient rendues au Seigneur) si bien que le mot
" domino " désigne maintenant le jeu.
Le modèle le plus courant sur le
marché est formé de 28 pièces comportant toutes les combinaisons des
nombres de 0 à 6 et allant du double-zéro (0, 0) au double-six (6,
6) : on l’appelle d’ailleurs le double-six. Les nombres sont
représentés par des points sur une face d’un prisme rectangulaire.
De votre jeu, sortez les six
dominos suivants : (1, 2), (1, 3), (1, 4), (2, 3), (2, 4), (3, 5).
Placez-les de façon à obtenir la
somme de 4 999.
32. De l’argent de poche
1e Agathe
a { dollars et
Caroline a Ä dollars.
Agathe et Caroline possèdent ensemble
81 dollars. Par ailleurs, Agathe possède 11 dollars de plus que Caroline.
Combien chacune
possède-t-elle ?
2e Carole possède
s dollars. Nicolas
sait que s/3
+ s/7 = 60
dollars.
Quel est l’avoir de
Carole ?
3e Réjean possède £
dollars et Rollande possède H
dollars. Ensemble, ils possèdent 60 dollars. Par
ailleurs, £/H
+ 60/H = H/6.
Combien chacun
possède-t-il ?
33. Les jetons de Mireille
Mireille a donné le problème
suivant à un garçon de sept ans.
- Découpe 12 jetons. Numérote-les de 1 à 12. Place maintenant un jeton
sur chacune des 12 cases ci-dessous de façon à effectuer des additions
qui donnent les sommes 12, 11, 10 et 6. Après plusieurs essais, le jeune
garçon trouva cette disposition.
|
3 |
|
4 |
|
2 |
|
1 |
|
+
|
|
+
|
|
+
|
|
+
|
|
9 |
|
7 |
|
8 |
|
5 |
|
12
|
|
11
|
|
10
|
|
6
|
Trouvez une disposition avec les
sommes 12, 11, 9 et 7.
34. Les arbres de Newton
Le problème suivant est dû au
britannique Isaac Newton (1642-1727) qui fut tour à tour mathématicien,
physicien, astronome et philosophe anglais.
Neuf arbres sont disposés de
façon à former huit rangées de trois arbres en ligne droite comme
ci-dessous : trois rangées horizontales, trois verticales et deux
diagonales.
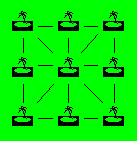
Disposez maintenant ces neuf
arbres pour qu’ils forment 10 rangées de trois arbres en ligne droite.
35. Les timbres de Jean-Christophe
Jean-Christophe doit timbrer quatre
colis. Il doit mettre quatre timbres sur chaque colis et utiliser en
tout :
• quatre timbres de 1 $
• quatre timbres de 2 $
• quatre timbres de 4 $
• quatre timbres de 8 $
Le coût des timbres pour chaque
colis est respectivement de 9 $, de 13 $, de 17 $ et de
21 $.
Quels timbres Jean-Christophe
devra-t-il utiliser pour chaque colis ?
36. Chiffres cachés
Dans le tableau ci-dessous, chaque
lettre a une valeur différente de 0 à 9. Un groupe de deux ou de trois
lettres forme un nombre. De plus, les nombres sont additionnés
horizontalement et verticalement.
|
A B |
+ |
C D |
= |
E F |
|
+ |
|
+ |
|
+ |
|
G H |
+ |
J G |
= |
B G |
|
=
|
|
=
|
|
=
|
|
D B |
+ |
F J |
= |
C G K |
Une des lettres A, H ou K vaut 0,
l’autre 6 et le troisième 7.
Décodez le tableau en trouvant le
chiffre correspondant à chaque lettre.
37. Quel est leur âge ?
Neuf personnes disposées 3 × 3
donnent chacune leur âge. Yann a noté que la personne du centre avait 14
ans, mais il a oublié le reste.
Il sait toutefois que :
1. La somme des âges égale 42 ans horizontalement, verticalement et en
diagonale.
2.
La personne au centre de la première rangée horizontale est
respectivement deux fois et quatre fois plus jeune que ses deux voisines
sur cette même rangée.
Déterminez l’âge des huit
autres personnes.
38. Secrets à découvrir
Trois amies : Bertrande,
Gertrude et Laurence ont ensemble 67 ans. Elles demeurent l’une à
Matane, l’autre à Rimouski et la troisième à Sept-Îles. Lors de leur
dernière rencontre, elles ont vérifié leur avoir et ont constaté qu’elles
possédaient 1 000 $ répartis ainsi : 200 $,
300 $ et 500 $.
1.
La Matanaise est plus jeune que Gertrude.
2.
Bertrande est plus âgée que la Rimouskoise.
3.
Celle qui a le moins d’argent est âgée de 25 ans.
4.
Celle de 20 ans n’a jamais vu Sept-Îles.
5.
La Rimouskoise a plus d’argent que Laurence.
Trouvez l’âge, le lieu de
résidence et l’avoir de chacune.
|
|
Âge |
Résidence |
Avoir |
|
Bertrande |
|
|
|
|
Gertrude |
|
|
|
|
Laurence |
|
|
|
39. Une visite à la campagne
Annie possède, à la campagne, un
champ triangulaire dont chaque côté mesure 300 mètres.

Elle a l’intention de diviser
son terrain en six lots en vue de les vendre. Trois lots seront de forme
triangulaire et identiques. Les trois autres, également identiques,
auront la forme d’un losange.
Comment Annie partagera-t-elle son
champ ?
40.
Les inquiétudes de Philippe
- As-tu une calculatrice, Valérie
?, lança Philippe arrivé à l’improviste.
-
Bien sûr, répondit Valérie, que veux-tu en faire ?
-
Voilà, prends ta calculatrice. Tu entres, par exemple, 324. Puis, tu
utilises les quatre opérations (+, - , ´
, ¸ ) dans la séquence
que tu désires avec le nombre 12.
-
Si j’ai bien compris, après avoir entré 324, je peux, par exemple,
additionner 12, diviser par 12, soustraire 12 et multiplier par 12.
-
C’est bien cela.
-
Je lis alors 192 sur l’écran d’affichage.
-
Moi, je voudrais savoir combien il y a de séquences comportant les quatre
opérations, qui produisent un résultat supérieur à 324.
Aidez Philippe à déterminer ces
séquences. |
|
|
![]()
![]()