Ceci est le cinquième livre édité par Récréomath.

Évasions calculées
80 problèmes mathématiques et logiques

Par Charles-É. Jean

Solutions 1 à 40

Solutions 41 à 80

Solution 1. Denis ouvrit la première porte le 10^e jour. Le même jour, il essaya une clé dans la deuxième porte. C’est donc au 18^e jour qu’il ouvrit la 2^e porte, puis au 25^e jour la troisième porte et ainsi de suite en prenant un jour de moins par porte.

Denis ouvrira la dernière porte le 46^e jour, soit le 10 juin.

Solution 2. Une disposition possible est :

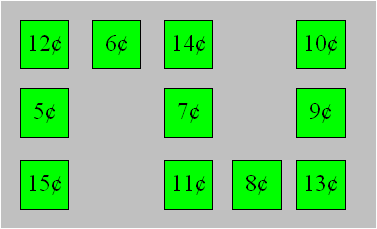
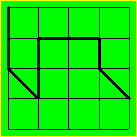
Solution 3. Réginald doit débourser au moins 7,35 $. Voici un chemin possible :

Solution 4. Voici quatre étapes pour ramener les deux hommes et la Constitution sur la terre ferme :

1^e Le batelier amène Lévesque sur la terre ferme et lui demande de l’attendre.

2^e Le batelier retourne sur l’île et revient avec Trudeau.

3^e Le batelier ramène Lévesque sur l’île, le laisse là et revient avec la Constitution.

4^e Le batelier retourne sur l’île et revient avec Lévesque.

Solution 5. Le taux de vérité de chaque enfant est :

Comme Michel et Sandra disent plus souvent la vérité, Michel est le troisième et Sandra la deuxième. Donc Louise est l’aînée et Germain est le cadet.

L’ordre, en commençant par l’aînée, est : Louise, Sandra, Michel et Germain.

Solution 6. Valin prendra 12 jours au minimum. Quatre chemins sont possibles :

1^e AG, GH, HF, FE, EB, BC, CF, FE, EB, BA, AG, GD

2^e AG, GH, HF, FC, CB, BE, EF, FC, CB, BA, AG, GD

3^e AB, BC, CF, FH, HG, GA, AB, BE, EF, FH, HG, GD

4^e AB, BE, EF, FH, HG, GA, AB, BC, CF, FH, HG, GD

Solution 7. Voici les résultats partiels et le résultat final dans chaque cas :

5 988 829

Les deux derniers chiffres sont 59 et les deux derniers 29. Il doit y avoir quatre 8 au centre. Le nombre cherché est 59 888 829.

1 222 155

Le premier chiffre est 1. Les trois derniers sont 144. Il doit y avoir quatre 2 au centre. Le nombre cherché est 12 222 144.

Solution 8. Il existe plusieurs dispositions. En voici une :

Solution 9. Les enfants de Louise et de Claude sont : Didier, Olivier et Serge. Les enfants d’Annie et Pierre sont : Marlène, Nathacha et Robin.

Solution 10. Voici un chemin qui permettra à chacun de traverser la rivière :

Solution 11. En faisant la somme des huit nombres qui touchent à un quantième donné, on s’aperçoit que la somme de ces nombres est égale à huit fois le quantième. Le quantième cherché est 168 ¸ 8 = 21.

Ginette est née le 21 avril.

Solution 12. L’addition reconstituée est : 234 + 889 + 621 = 1744.

Solution 13. Construisons un tableau qui permettra de voir les combinaisons dont la somme est paire (P) ou impaire (I).

Il y a donc 10 sommes paires et six sommes impaires. Comme la pièce est choisie au hasard, sur 16 dollars, Pierrette en gagnera 10 et Michel 6. Pierrette gagne donc 50 dollars et Michel 30 dollars.

Solution 14. Voici une disposition des nombres dans chaque cas :

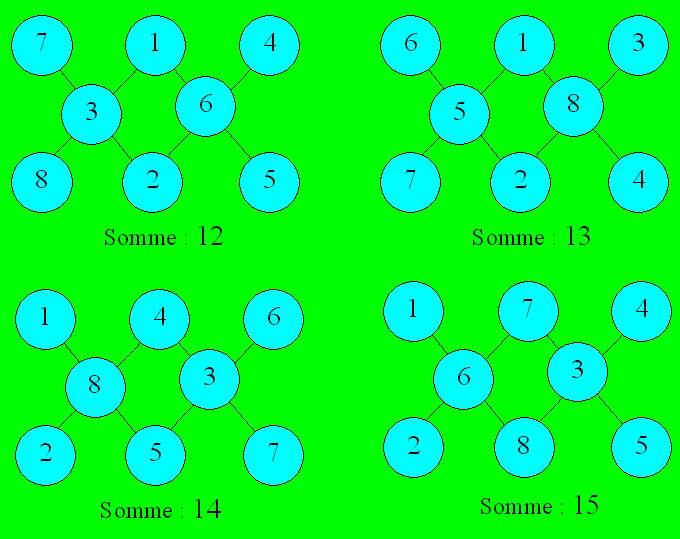
Solution 15. Gisèle est la plus âgée.

Solution 16. On voit le nombre de chemins qui aboutissent sur chaque case blanche de la rangée inférieure.

Sur la dernière ligne, la somme est 35. Il y a donc 35 chemins possibles.

Solution 17. Une disposition des nombres est donnée pour chaque résultat.

Solution 18. Il y a 25 façons de combiner les dés deux par deux. Le tableau ci-dessous indique les paires en ordre et la probabilité pour chaque somme.

Nicolas m’a berné en me faisant miroiter 5 sommes contre 4.

Solution 19. Après la première attaque, elle plaça trois soldats à chaque fenêtre des coins et cinq soldats à chaque autre fenêtre.

Après la seconde attaque, elle en plaça cinq à chaque coin et deux à chaque autre fenêtre.

Solution 20. Un chemin suivi par le gardien est :

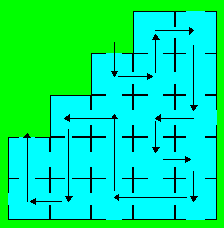
Solution 21. Si on additionne 100 + 99 + 98 + 97 + … + 3 + 2 + 1, il est certain que le calcul sera long. Pour simplifier, additionnons les boules des rangées extrêmes (la première et la dernière) ; éliminons ces deux rangées et additionnons les deux rangées extrêmes parmi celles qui restent (la deuxième et l’avant-dernière) ; en continuant ainsi, nous trouvons 50 fois la somme 101. Il y a donc 5 050 boules.

Solution 22. Voici un tableau qui illustre la situation :

Solution 23. Pour chaque grille, un exemple de chemin est donné de même que le maximum atteint.

Solution 24. Yves: 342 ¸ 13 = 26 tours et quatre kilomètres. Mia : 226 ¸ 13 = 17 tours et cinq kilomètres. Mia est la plus éloignée du point de départ. Donc, Mia a parcouru une plus grande distance dans son dernier tour.

Solution 25. Ceux qui se sont placés respectivement aux 6^e, 18^e et 24^e rangs ont été choisis.

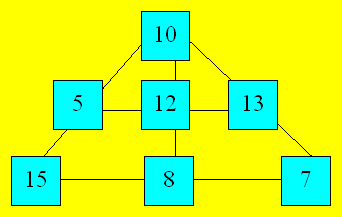
Solution 26. Comme il y a 30 billes dans chaque rangée, il doit y avoir 10 billes dans la section où trois rangées se rencontrent. En complétant, on obtient :

Solution 27. L’addition est : 632 + 632 = 1264.

Solution 28. La probabilité d’obtenir deux dés identiques est de 6 sur 36. Celle d’obtenir une somme plus grande que 8 est de 10 sur 36. Après 36 lancers, on aura :

Isabelle a gagné 60 $ et Alain 80 $.

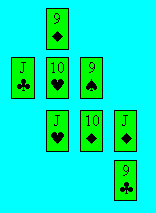
Solution 29. Voici la position des cartes :

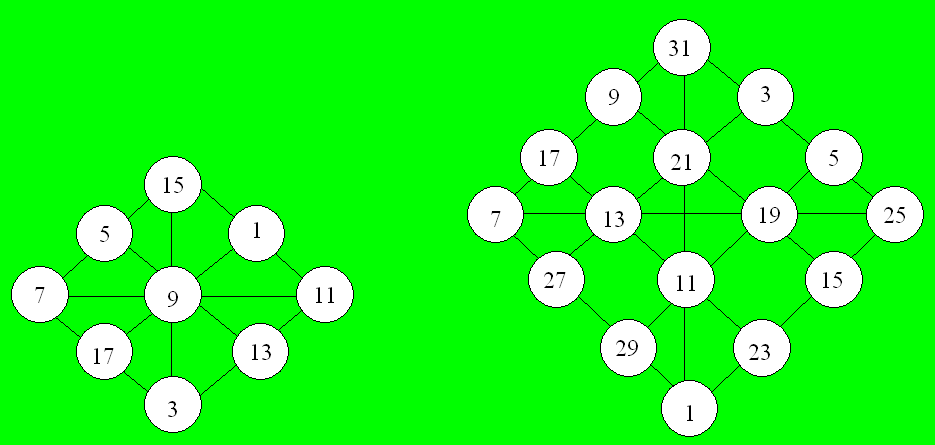
Solution 30. Voici la disposition des nombres dans chaque cas :

Solution 31. Voici une disposition possible :

Solution 32. 1^e Agathe a 46 $ et Caroline a 35 $.

2^e Carole possède 126 $.

3^e Réjean et Rolande ont respectivement 36 $ et 24 $.

Solution 33. Voici trois façons de disposer les nombres avec les sommes 12, 11, 9 et 7 :

a) 2 + 10 = 12, 3 + 8 = 11, 4 + 5 = 9, 1 + 6 = 7.

b) 2 + 10 = 12, 5 + 6 = 11, 1 + 8 = 9, 3 + 4 = 7.

c) 4 + 8 = 12, 1 + 10 = 11, 3 + 6 = 9, 2 + 5 = 7.

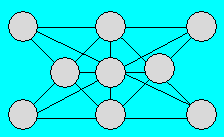
Solution 34. Les arbres peuvent être disposés ainsi :

Solution 35. Les quatre timbres par colis sont donnés.

Solution 36. Le tableau décodé ligne par ligne est : 65 + 19 = 84, 30 + 23 = 53, 95 + 42 = 137.

Solution 37. Si la personne située au centre de la première rangée horizontale a un an, les deux autres ont respectivement deux et quatre ans : ce qui fait une somme de sept ans. Puisque la somme est 42, la personne du centre a six ans et les deux autres ont 12 et 24 ans. Plaçons donc 12, 6 et 24 sur la première rangée horizontale et complétons pour donner 42 dans chaque rangée.

Les âges sont 2, 4, 6, 12, 16, 22, 24 et 26 ans.

Solution 38. Voici un tableau qui illustre la situation :

Solution 39. Le champ peut être partagé ainsi.

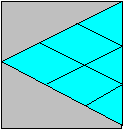
Solution 40. Il y a quatre séquences où le résultat est supérieur à 324 :