|
41. Des L
Dans une grille
carrée, on peut dessiner quatre L identiques, comme dans la figure placée à
gauche.
Dans la grille carrée de droite,
dessinez également quatre L identiques en utilisant 20 cases.
42. Des allumettes en triangles
Ces sept allumettes sont disposées en
deux triangles équilatéraux : un petit et un grand triangle.
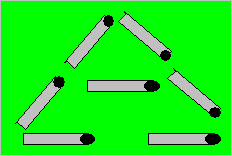
1e
Utilisez huit allumettes pour
construire trois triangles équilatéraux.
2e
Utilisez neuf allumettes pour construire cinq triangles équilatéraux.
3e
Utilisez 10 allumettes pour construire trois triangles équilatéraux.
43. Quelle heure est-il ?
Jai trouvé dans le grenier une
vieille horloge recouverte de poussière. Laiguille des minutes se trouvait
sur le 5 et laiguille des heures avait disparu. Jai également trouvé un
message au dos, probablement écrit par mon grand-père.
- Cette horloge sest arrêtée à
heures et 25 minutes le 12 mars 1922. Si tu veux savoir à quelle heure,
sers-toi des indices suivants :
Il
y a une chance sur trois que ce soit entre 3 heures et 6 heures.
Il
y a deux chances sur cinq que ce soit entre 4 heures et 7 heures.
Il
y a trois chances sur sept que ce soit entre 5 heures et 8 heures.
Il
y a quatre chances sur neuf que ce soit entre 6 heures et 9 heures.
44. Jongleries
Représentez
les nombres de 1 à 16 en utilisant les chiffres 1, 2, 3, et 4 pris une seule
fois dans chacun des cas. Vous pouvez utiliser les opérations +, - ,
×, ÷ de même que lélévation à une puissance. Aucune opération nest
obligatoire. Par exemple : 20 = 42 + 3 + 1.
|
1 |
|
9 |
|
|
2 |
|
10 |
|
|
3 |
|
11 |
|
|
4 |
|
12 |
|
|
5 |
|
13 |
|
|
6 |
|
14 |
|
|
7 |
|
15 |
|
|
8 |
|
16 |
|
45. Un nouveau stock
Marielle est propriétaire dun
magasin. Pour renouveler son stock,
Elle a acheté QR gilets à QR dollars chacun : ce qui a coûté QTM
dollars.
Elle a acheté M manteaux à TM dollars chacun : ce qui a coûté EPM
dollars.
Elle a dépensé RTS dollars pour acheter QS pantalons à RT dollars chacun.
Elle a dépensé BBTM dollars pour acheter CB blouses à BC dollars chacune.
Enfin, elle a acheté AT paires de souliers à AT dollars la paire pour un
montant de QEBQ dollars.
Heureusement, le grossiste sait quà
chaque lettre correspond un chiffre et que M = 6.
Quel est le montant total de la commande
de Marielle ?
46. Un groupe délèves
Dans un groupe, il y a 16 élèves. Les
prénoms sont : Luc, Réal, Diane et Victor. Les noms de famille
sont : Dion, Rioux, Lepage et Vignola. Aucun étudiant na le même nom.
Les 16 élèves doivent écrire leur nom sur un tableau carré de 16 cases. Dans
une même rangée horizontale, verticale et diagonale, les prénoms doivent
être différents et les noms de famille aussi.
|
Luc
Vignola |
|
|
|
|
|
|
|
Luc
Dion |
|
|
Luc
Rioux |
|
|
|
|
|
Luc
Lepage |
|
À quel endroit, les 12 autres élèves
écriront-ils leur nom lorsque les quatre Luc auront placé le leur ?
47. Des Sept-Îliens
Nom des garçons : Alex, Bastien,
Camille, Daniel.
Nom des filles : Fabienne, Geneviève, Héloïse, Irène.
Résidence des garçons : Comeau, Giasson, Régnault, Smith.
Résidence des filles : Arnaud, Brochu, Dequen, Évangéline.
1.
Héloïse ne demeure pas rue Dequen.
2.
Camille est lami de la fille qui demeure rue Arnaud.
3.
Daniel nest pas lami de Fabienne et nest jamais allé rue Régnault.
4.
La fille de la rue Évangéline est lamie du garçon de la rue Comeau.
5.
Lamie de Bastien demeure rue Dequen.
6.
Fabienne rencontre son ami rue Arnaud, où elle habite.
7.
Héloïse nest pas lamie de Daniel et nest pas lamie du garçon de
la rue Giasson.
8.
Le garçon de la rue Régnault est lami de Geneviève.
9.
Irène demeure rue Évangéline.
Déterminez dans quelles rues demeurent
chacun des garçons et des filles.
48. Des gains au cribbage
Gilles joue au
cribbage tous les jours, sauf le 16 de chaque mois et le lundi. À chaque fois
quil se livre à sa passion, Gilles joue 12 parties, sauf le 29 de chaque
mois et le mardi où il ne joue que six parties. Gilles gagne une partie sur
trois, sauf le 21 de chaque mois et le vendredi où il perd une partie sur
trois. Voici la page de calendrier de janvier :
|
D |
L |
M |
M |
J |
V |
S |
|
|
|
|
|
|
1 |
2 |
|
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
10 |
11 |
12 |
13 |
14 |
15 |
16 |
|
17 |
18 |
19 |
20 |
21 |
22 |
23 |
|
24 |
25 |
26 |
27 |
28 |
29 |
30 |
|
31 |
|
|
|
|
|
|
Combien de parties de cribbage Gilles
a-t-il gagné pendant les trois premiers mois de lannée 1982 ?
49. Les mesures de Tartaglia
Il semble bien que cest litalien
Niccola Fontana (1499-1557), connu sous le nom de Tartaglia, qui proposa le
premier un problème consistant à mesurer du liquide par transvasement.
Un marchand doit partager 24 litres dune
huile précieuse en trois parties égales. Les seules mesures disponibles sont
des récipients de 5, 11 et 13 litres, sans oublier évidemment celui de 24
litres.
Comment le marchand sy prendra-t-il
pour atteindre son but ?
50. Pas encore millionnaires
Six partenaires se rencontrent et
divulguent le montant de leur avoir qui, pour chacun, varie entre
100 000 $ et 1 000 000 $. Les six montants sont formés
des six mêmes chiffres, placés toutefois dans un ordre différent et aucun deux
napparaissant plus dune fois dans un montant. Par exemple, chaque montant
pourrait être composé de 1, 4, 5, 6, 8, 9 ordonnés de manières diverses.
Rencontrant Hélène, Aimée tente de
lui faire deviner le capital de chacun en lui disant ceci :
- Karine et Émilie possèdent respectivement trois et quatre fois mon avoir.
Bertrand, Dany et Firmin détiennent respectivement deux fois et demie, trois
fois et demie et cinq fois et demie mon avoir. Le dernier chiffre de la somme
que je possède est 6.
Hélène réfléchit, griffonne quelques
calculs simples et court chercher sa calculatrice.
Aidez Hélène à déterminer lavoir
de chacun.
51. Des figures en boules
La figure ci-dessous est formée par 16
boules et 24 segments de droite. On y compte neuf petits carrés égaux et
distincts.
Toujours à partir de la figure
initiale, vous devez enlever des boules et des segments pour constituer des
carrés disposés différemment.
1e
Enlevez 5 boules et 11 segments pour obtenir trois carrés.
2e
Enlevez 4 boules et 8 segments pour obtenir cinq carrés.
3e
Enlevez 6 boules et 12 segments pour obtenir trois carrés.
4e
Enlevez cinq boules et 12 segments pour obtenir deux carrés.
52. Un parterre de fleurs
Lan passé, Martine avait partagé son
parterre en 10 parcelles. Dans la rangée de la base, elle avait planté cinq,
sept, huit et trois fleurs. Dans chaque parcelle des autres rangées, elle avait
placé le total des fleurs qui se trouvaient dans les deux parcelles
inférieures voisines. Ainsi, dans la deuxième rangée, on trouvait 5 + 7 = 12
fleurs ; 7 + 8 = 15 fleurs et 8 + 3 = 11 fleurs.

Cette année, Martine a divisé son
parterre en 15 parcelles et a planté 168, 88, 47, 25 et 13 fleurs dans les
parcelles qui touchent à la zone A comme il est montré ci-dessous. On ne
connaît pas le nombre de fleurs des autres parcelles ; mais ce nombre a été
déterminé à partir de la base, selon le même principe que lannée
précédente.

Combien y a-t-il de fleurs en tout dans
les cinq parcelles qui touchent à la zone B ?
53. Un voyage organisé
Dans lorganigramme, suivez les
flèches et effectuez les opérations indiquées. Les lettres x, y,
z peuvent changer de valeur en cours de route. À la fin, vous trouverez
un nombre.
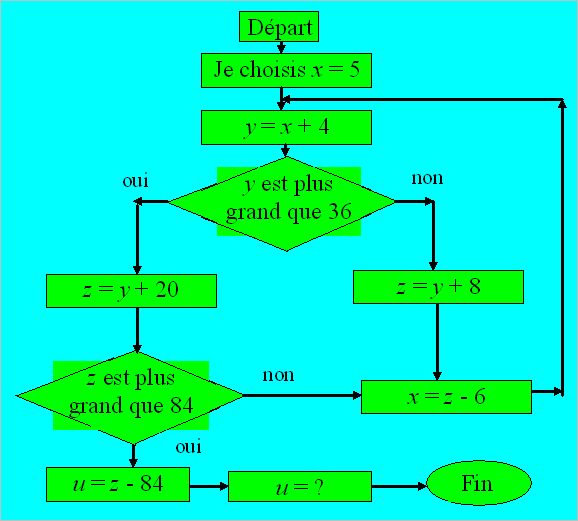
Quel est le nombre qui correspond à u
?
54. Des comités disloqués
Quatre
comités, A, B, C, D, sont composés chacun de quatre personnes qui sont
président(e), vice-président(e), secrétaire, trésorier(ère).
Les
président(e)s sont : Andrée, Bernard, Céline, Denis.
Les
vice-président(e)s sont : Élisabeth, Francis, Ginette, Henri.
Les
secrétaires sont : Isabelle, Jérôme, Lorraine, Mathieu.
Les
trésoriers(ères) sont : Nathalie, Oscar, Paule, Roger.
Les sept personnes suivantes disent deux
phrases dont lune est vraie et lautre fausse.
Lorraine :
Je suis dans le même comité que Mathieu. Je suis dans le comité C, comme
Francis.
Francis :
Je suis dans le même comité que Paule. Je suis dans le comité B.
Nathalie :
Je suis trésorière du comité C. Je suis dans le comité A, comme Céline.
Roger :
Je suis dans le comité D, comme Denis. Je suis dans le comité A.
Oscar :
Je suis dans le comité D. Je suis dans le même comité que Bernard et
Isabelle.
Élisabeth :
Je suis dans le même comité que Lorraine. Je suis dans le même comité que
Denis et Jérôme.
Ginette :
Je suis dans le même comité que Mathieu. Je suis dans le même comité que
Paule.
Dans quel comité se trouve Henri ?
55. En forêt
Dans une forêt, 11 arbres sont disposés
comme ci-dessous. Régis désire faire la coupe de ces arbres et partager le
tronc en billes dun mètre de longueur. Après avoir mesuré ces 11 arbres,
il réalise que chaque rangée de trois arbres alignés obliquement contient 26
billes et que les arbres des coins peuvent donner 8, 9, 12 et 13 billes, comme
il est indiqué.
De plus, aucun arbre ne peut donner le
même nombre de billes, lesquelles varient de 4 à 14 dun arbre à lautre.
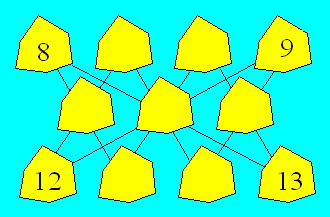
Déterminez le nombre de billes par
arbre.
56. Lettres et chiffres
1e Pendant
un bon moment, Réal sest amusé à écrire les 26 lettres de lalphabet,
dans lordre où il se présente, et à répéter la série jusquà ce quil
ait inscrit 10 000 lettres.
a b c d e f g h i j k l m n o p q r s t u
v w x y z a b c d e f g h i
Quelle est la dernière lettre écrite ?
2e Puis, il décide décrire
les nombres les uns à la suite des autres.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
18 19
Parvenu au nombre 18, Réal a déjà
écrit 27 chiffres, comme on peut le vérifier. Il cessa après avoir écrit
10 000 chiffres.
Quel est le dernier chiffre écrit ?
57. Neuf dépôts
Neuf personnes ont déposé un certain
montant dargent dans un coffre-fort muni de neuf cases. Le nom des déposants
apparaît sur chaque case.
|
Armande
|
Brigitte
|
Carol
|
|
David
|
Étienne
|
François
|
|
Gonzague |
Henriette |
Irma
|
Armande et Carol ont déposé
995 $; Carol et Irma : 695 $; Irma et Gonzague : 665 $;
Gonzague et Armande : 965 $. Dans chaque rangée de trois cases
horizontalement, verticalement et en diagonale, le montant total est de
1 245 $.
Combien chaque personne a-t-elle
déposé ?
58. Lallocation de Christian
Christian est absorbé par ses calculs.
Son père lui a promis une allocation hebdomadaire identique au nombre de
diviseurs dun certain entier entre 9 et 59. Christian sait que, par exemple,
35 a quatre diviseurs : 1, 5, 7, 35 ; que 16 en a cinq : 1, 2, 4, 8,
16.
Évidemment, le jeune garçon veut que
le montant de son allocation soit le plus élevé possible. Aussi recherche-t-il
le nombre qui a le plus de diviseurs. Le père, lui, connaît le montant exact
car il a, au préalable, vérifié avec lordinateur. Évidemment, il a dû
composer un programme.
Quel est le montant maximum que
Christian pourra toucher ?
59. Des mots multipliés
En recopiant deux problèmes de multiplication, Julie a remplacé les nombres
par des mots. Toutefois, dans chaque cas, elle a laissé le résultat. De plus,
chaque même lettre est mise pour un même chiffre.
1e C A R × A R C = 47 385
2e M O N
× N O M = 675 783
Écrivez R O C en chiffres. Au besoin,
utilisez votre calculatrice.
60. La semaine de six jours
Geneviève-Marie a décidé de supprimer
le vendredi au calendrier et de créer ainsi des semaines de six jours. Voici lexemple
dun mois :
|
D |
L |
M |
M |
J |
S |
|
|
|
1 |
2 |
3 |
4 |
|
5 |
6 |
7 |
8 |
9 |
10 |
|
11 |
12 |
13 |
14 |
15 |
16 |
|
17 |
18 |
19 |
20 |
21 |
22 |
|
23 |
24 |
25 |
26 |
27 |
28 |
|
29 |
30 |
31 |
|
|
|
1e Si le 3 mai tombe un
samedi, quel jour de la semaine sera le 30 ?
2e Le 1er janvier
1984 tombe un lundi. Quel jour de la semaine sera le 29 décembre de la même
année.
3e Odette est née un jeudi 5
avril 1970. En quelle année son anniversaire de naissance sera-t-il à nouveau
un jeudi ?
61. Un divin arrangement
- Tu vois cet arbre, fit remarquer
Sylvain. Il possède 10 branches. Le nombre de ses feuilles dune branche à lautre
suit un ordre logique. Malheureusement, les feuilles des deux branches
supérieures sont tombées.
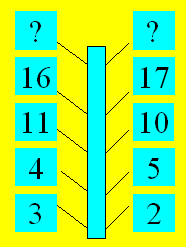
Combien y avait-il de feuilles sur larbre
avant quil ne commence à les perdre ?
62. En parcelles
Lucie a un terrain de 60 mètres sur 40
mètres. Elle plante un piquet tous les 10 mètres et obtient ainsi 24 parcelles
carrées. Lucie attache un fil dacier à un piquet planté dans un coin et
désire ainsi clore le plus grand nombre de parcelles sans couper son fil.

Combien de parcelles Lucie pourra-t-elle
clôturer sans avoir à mettre son fil en double ?
63. Une planète protégée
Voici le plan secret dune zone de
protection dune planète. Plusieurs visiteurs ont jusquà ce jour péri à
lintérieur de ses murs parce quils avaient choisi un mauvais mot de
passe.
Lorsque vous visiterez ce château fort,
à la ligne de départ vous devrez choisir un mot de passe, lequel est un nombre
entier entre 100 et 200. Vous devrez suivre le chemin indiqué et effectuer
chaque opération. À la fin, vous devrez retrouver le même nombre quau
départ sinon vous serez pulvérisé.
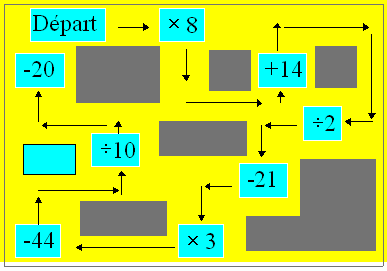
Quel est ce mot de passe ?
64. Une loterie
Cinq bouliers contiennent chacun cinq
boules numérotées de 1 à 5. On tire dans lordre une boule dans chaque
boulier, afin de former un numéro gagnant de cinq chiffres. Une personne gagne
lorsque le nombre formé est un carré parfait. Ainsi 34 225 est un numéro
gagnant car : 185 ´ 185
= 34 225.
Martin décide de miser 1 $ et il
recouvre 300 fois sa mise sil tire un numéro gagnant.
Selon toute probabilité, Martin peut-il
espérer gagner beaucoup dargent ?
65. Cartes chiffrées
Voici les quatre couleurs du jeu de
cartes : ♠, ♣, ♥, ♦.
Chaque couleur correspond à un chiffre sauf le 0 ou le 9.
Deux couleurs accolées forment un nombre de deux chiffres.
♥ ♠ +
♥ ♦ = ♠
♣
♥ ♥ + ♣
♣ =
♠ ♠
♠ ♠ + ♣
♣ = ♦ ♦
En vous basant sur ces égalités,
déterminez le chiffre correspondant à chaque couleur.
66. Une division cachée
La plupart des gens se souviennent davoir
appris la division à lécole. Même si la disposition des nombres varie dune
méthode à lautre, le vieux principe de multiplier par un nombre choisi, de
soustraire et dabaisser un chiffre a toujours été très populaire.
Ceci est lexemple de la division de 6
318 par 22.
|
6318
|
|22 |
|
44 |
287 |
|
191
176 |
|
|
158
154 |
|
|
4 |
|
La réponse est 287 reste 4.
Voici maintenant la division dun
certain nombre par 7 où chaque astérisque remplace un chiffre :
|
4*** |
|7 |
|
** |
*** |
|
3*
** |
|
|
5*
** |
|
|
5 |
|
Reconstituez la division.
67. Une chocolaterie
Michèle est responsable de la mise en
marché dans une chocolaterie. On lui a demandé de mettre au point un système
permettant de combiner dans une même boîte diverses variétés de chocolats.
Elle a en stock les variétés suivantes : à la fraise (classe 1), à la
framboise (classe 2), au bleuet (classe 3) et à la groseille (classe 4).
Michèle doit placer 36 chocolats par
boîte en y mettant une quantité différente de chaque classe. Les chocolats de
classe 1 doivent être moins nombreux que ceux de classe 2 et ainsi de suite,
selon lordre des classes. Il doit y avoir au moins trois chocolats à la
fraise dans une même boîte.
À titre dexemple, voici ci-dessous
trois combinaisons permettant de préparer trois boîtes :
|
Fraise |
Framboise |
Bleuet |
Groseille |
|
3 |
5 |
6 |
22 |
|
4 |
7 |
11 |
14 |
|
3 |
9 |
11 |
13 |
Combien Michèle peut-elle préparer de
boîtes de chocolats ?
68. Cartes logiques
Dune rangée verticale à lautre,
les cartes sont placées selon un ordre logique.
|
3© |
|
4© |
|
6© |
|
7© |
|
? |
|
5¨ |
|
8¨ |
|
1¨ |
|
4¨ |
|
? |
Nommez les deux cartes de la dernière
rangée.
69. Les quadrilles de Lucas
Édouard Lucas (1842-1891) proposa une
variante célèbre du jeu des dominos. Il sagit de placer les 28 pièces dun
ensemble double-six de telle sorte que quatre points identiques forment un
carré. La première et la dernière rangée horizontale contiennent chacune
quatre carrés tandis que les deux rangées intermédiaires contiennent chacune
trois carrés. Selon le concepteur de ce problème, il existe 342 740
façons de quadriller cette figure. En voici un exemple :
|
0 |
0 |
3 |
3 |
4 |
4 |
1 |
1 |
|
0 |
0 |
3 |
3 |
4 |
4 |
1 |
1 |
|
|
5 |
5 |
6 |
6 |
0 |
0 |
|
|
|
5 |
5 |
6 |
6 |
0 |
0 |
|
|
|
4 |
4 |
5 |
5 |
2 |
2 |
|
|
|
4 |
4 |
5 |
5 |
2 |
2 |
|
|
2 |
2 |
6 |
6 |
1 |
1 |
3 |
3 |
|
2 |
2 |
6 |
6 |
1 |
1 |
3 |
3 |
Prenez vos 28 dominos et reconstituez ce
tableau en indiquant la position exacte de chaque pièce. Par la suite, vous
pourrez essayer de trouver dautres quadrilles.
70. Le gâteau de Pascal
Pascal vient de réussir un immense
gâteau de forme circulaire, qui semble très appétissant. Lucille sapproche
et lui dit :
- Peux-tu diviser ce gâteau au moyen de 20 traits de couteau en ligne droite dune
extrémité du gâteau à lautre, en partant toujours du point darrivée ?
Tu dois ainsi obtenir le plus grand nombre de morceaux. Voici un exemple de
partage :

Combien de morceaux Pascal pourra-t-il
obtenir ?
71. Le collier de Louise
Louise avait un collier de 48 perles de
grande valeur. Un inconnu subtilisa le collier et le modifia au hasard de telle
sorte quune perle sur quatre de rang impair était fausse et quune perle
sur trois de rang pair était authentique. Puis, il replaça le collier dans le
coffre.
Par la suite, Louise voulut réduire la
longueur du collier. Elle décida denlever une perle de cinq en cinq, à
partir de la 7e perle jusquà la 37e.
Selon toute probabilité, combien
restait-il de perles authentiques dans le collier de Louise ?
72. Des disques
1e Pierre et Réjeanne ont
respectivement o et m
disques. Réjeanne a cinq disques de plus que Pierre.
Aussi, (o ´ o)
+ (m ´
m) = 377.
Combien Pierre et Réjeanne ont-ils de
disques ensembles ?
2e Paul,
Martine et Lucie ont respectivement l,
u et n
disques. Par ailleurs, Paul et Martine ensemble ont six
disques de plus que Lucie. Aussi, (l ´
l) + (u ´
u) = (n ´
n).
Combien chacun a-t-il de disques,
sachant que Lucie en a deux de plus que Martine ?
73.
Cest parfait
- Savais-tu, Denise, quil existe des
nombres parfaits ?
-
Des nombres par
faits ?
-
En effet, 6 est parfait.
-
Pourquoi ?
-
Parce que la somme de ses diviseurs est 6.
-
Attends un peu. Les diviseurs de 6 sont 1, 2, 3 et 6. Ça fait 12 et non 6.
-
Tu ne dois pas tenir compte du nombre lui-même. Donc, tu additionnes 1, 2 et 3
et tu obtiens 6. Cest dailleurs le plus petit nombre parfait.
-
Y a-t-il dautres nombres parfaits ?
-
Oui, seulement douze nombres parfaits sont connus. Le troisième est 496 et le
quatrième 8 128.
-
Ça va, je comprends.
- Peux-tu alors trouver le deuxième
nombre parfait ? Je te donne un indice : il ne dépasse pas 100.
74. Chacun sa part
Dans chacun des cas, chaque lettre
différente représente un chiffre.
1e
Maxime veut partager également AM3 726 dollars entre huit
personnes. Par hasard, il na pas de monnaie. Combien restera-t-il de dollars
non partagés ?
2e
Manon partage également WXY WXY livres entre sept personnes.
Combien de livres ne seront pas partagés ?
3e
Genevière partage également RS4 832 cahiers entre 125 enfants.
Combien de cahiers ne seront pas partagés ?
4e Yolande
partage également LOT + MER fleurs entre trois personnes. Combien de fleurs ne
seront pas partagées, puisque LOT ¸
MER = 8 ?
75. Sous le signe du chat
Ernö Rubik, un architecte hongrois,
créa un cube qui révolutionna le marché du jouet au début des années 1980.
En effet, des millions dexemplaires furent vendus à travers le monde. Des
centaines darticles de revues furent écrits sur le sujet de même que des
dizaines de livres.
Certains appellent le cube lalgorithme
de Dieu, dautres le jeu du siècle. Quoiquil en soit, la cubomanie sest
répandue à une allure vertigineuse dans tous les pays. Une dépêche de la
presse canadienne (82 - 04 - 10) a même rapporté quun journal chinois avait
dû mettre en garde ses lecteurs contre les dangers du cube. Il semblerait que
le cube aurait provoqué des divorces, des douleurs articulaires, de lhypertension
et de sérieux écarts de conduite.
Prenez votre cube et écrivez le mot
CHAT. Pour chaque lettre, vous partez toujours du cube dans sa position
originale, cest-à-dire lorsque chacune des six faces est de couleur
uniforme. Voici dailleurs la représentation que vous devez obtenir, en
supposant que seulement deux couleurs devraient apparaître sur une face pour
chaque lettre. Voici les faces :

Tenez votre cube toujours dans la même
position de façon quà la fin la face illustrée soit devant vous.
76.
Des ziades
Des habitants dune petite ville ont
inventé une nouvelle façon dexprimer les nombres. Ils comptent ainsi :
- zéro, un, deux,
-
une triade, une triade un, une triade deux,
-
deux triades, deux triades un, deux triades deux,
-
une viade, une viade un, une viade deux
-
une viade une triade, une viade une triade un, une viade une triade deux,
-
une viade deux triades, une viade deux triades un, une viade deux triades deux,
-
deux viades, deux viades un, etc.
Après deux viades deux triades deux, on
retrouve une xiade. Et après deux xiades deux viades deux triades deux, on
retrouve une ziade.
Un habitant de cette ville possède deux
ziades une xiade une triade deux chevaux.
Combien cet habitant a-t-il de chevaux ?
77. Un héritage
Martin est père de six garçons et de
sept filles. Ayant lintention de partager son avoir entre ses enfants, il se
dit :
Si je partage tout mon argent également entre mes six garçons, il me restera
cinq dollars.
Si je partage tout mon argent également entre mes sept filles, il me restera
six dollars.
Si je partage tout mon argent également entre mes 13 enfants, il me restera 12
dollars.
Par ailleurs, si je partage tout mon argent également entre mes 41 neveux et
nièces, il ne me restera rien.
Quel est lavoir de Martin ?
78.
Des plaques dimmatriculation
Dans une ville, les plaques dimmatriculation
sont composées dun nombre de trois chiffres, de la lettre P et dun second
nombre de trois chiffres. Par exemple, 461 P 529 est possible. On a décidé
ceci :
1.
La somme des deux nombres doit être inférieure à 1 000.
2.
Aucune plaque ne doit avoir deux nombres identiques ni un nombre inférieur à
100.
Par exemple, les plaques suivantes nexistent
pas :
|
236 P 842 |
247 P 247 |
350 P 047 |
Déterminez le nombre possible de
plaques.
79. Des chars allégoriques
Lors du dernier carnaval, il y avait 12
chars allégoriques. Les chars étaient numérotés de 1 à 12 et ils
contenaient un nombre de personnes correspondant au numéro.
Éric
fut frappé par le fait que les numéros des chars nétaient pas en ordre. De
plus,
1.
Chaque groupe de deux chars transportait le même nombre de personnes.
2.
Il y avait 19 personnes dans les trois premiers chars, 20 dans les trois
suivants, 21 dans les trois autres et 18 dans les trois derniers.
3.
Les numéros des deuxième, sixième, huitième, douzième chars étaient
consécutifs en ordre croissant. Par exemple 16, 17, 18, 19 sont des nombres
consécutifs en ordre croissant.
4.
Le deuxième char contenait plus de personnes que le premier.
Déterminez le numéro de chaque char.
80. Variation sur le cube de Rubik
Le jeu du cube de Rubik consiste à
agencer les six faces de telle sorte que chacune delles présente une couleur
uniforme. Pour cette variante du jeu, il faut placer dabord le cube dans
cette position finale.
Lorsque chaque face présentera une
seule couleur, procédez aux déplacements indiqués en faisant chaque fois un
demi-tour. Tenez toujours le cube dans la même position.

Reprenez trois fois de suite cette même
séquence. Puis effectuez la séquence suivante en faisant chaque fois un
demi-tour.

Le cube sera alors mélangé comme
désiré.
Vous devez remettre le cube dans sa
position finale en limitant au minimum le nombre des manipulations. |
![]()
![]()