Solution 41. Voici une grille comportant quatre L :

Solution 42. Voici des triangles construits dans chaque cas :

Solution 43. Pour chaque intervalle d’une heure, établissons la probabilité.

La somme des probabilités est plus grande entre 6 et 7 qu’entre 5 et 6, car 4/27 est plus grand que 1/9. L’horloge s’est arrêtée à six heures et 25 minutes.

Solution 44. Il peut exister plus d’une solution par nombre représenté.

1 = (2 - 1)(4 - 3)            2 = (4 + 2) - (3 + 1)            3 = 2³ - 1 - 4

4 = (1 + 2 + 4) - 3          5 = 3² - 4¹                                  6 = (3 × 4) ¸ (1 ´ 2)

7 = 2³ - 1⁴                            8 = 3² - 1⁴                          9 = 2³ + 1⁴

10 = 3² + 1⁴                      11 = 2³ + 4 - 1                    12 = 2³ + 4¹

13 = 2³ + 1 + 4            14 = (3 × 4) + (1 × 2)          15 = (3 × 4) + 1 + 2

16 = (12 × 4) ÷ 3

Solution 45. Puisque QR × QR = QTM et M = 6, alors R = 4 et T = 9.

Puisque M × TM = EPM, alors E = 5 et P = 7.

Puisque QS × RT = RTS, alors S = 0.

Puisque CB × BC = BBTM, alors B = 2 et C = 8.

Puisque AT × AT = QEBQ, alors A = 3.

Marielle a dépensé successivement 196 $, 576 $, 490 $, 2 296 $, 1 521 $ pour un total de 5 079 $.

Solution 46. Voici un tableau qui illustre une situation :

Solution 47. Comme le nom des filles est cité plus souvent que celui des garçons, il est plus facile de commencer avec leurs noms.

Solution 48. Construisons un tableau qui indique la fréquence et le nombre de parties gagnées pour chaque jour de la semaine en prenant soin d’exclure les 16, 21 et 29 de chaque mois.

Aucune partie n’est jouée le 16 de chaque mois. Huit parties sont gagnées le 21 de chaque mois. Quatre parties sont gagnées le 29 janvier ; il n’y a pas de 29 février ; aucune partie n’est gagnée le 29 mars, car c’est un lundi. Gilles a donc gagné 28 parties les 16, 21 et 29. Il a donc gagné 334 parties en tout.

Solution 49. Voici une façon de transvaser le liquide :

(1) Le contenant de 11 litres est rempli à même celui de 24 litres.

(2) Le contenant de cinq litres est rempli à même celui de 24 litres.

(3) Le contenant de cinq litres est versé dans celui de 13 litres.

(4) Le contenant de 13 litres est complété à même celui de 11 litres.

(5) Le contenant de cinq litres est rempli à même celui de 13 litres.

(6) Le contenant de cinq litres est versé dans celui de 11 litres.

Solution 50. Le dernier chiffre de chaque montant est :

Les six chiffres sont donc, 1, 3, 4, 5, 6, 8. On connaît le premier et le dernier chiffre du montant de chacun. En faisant des essais avec les quatre autres chiffres, on trouve :

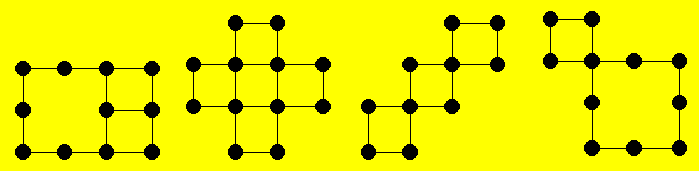
Solution 51. Voici une figure obtenue dans chaque cas :

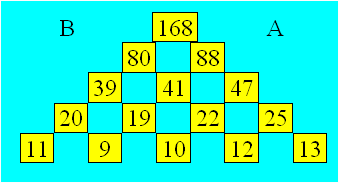
Solution 52. Il y a 318 fleurs dans les parcelles qui touchent à la zone B.

Solution 53. Après avoir trouvé les valeurs de x, de y et de z, on aboutit à u = 11. Ce problème peut être résolu par ordinateur.

Solution 54. Voici un tableau qui illustre la situation :

Henri se trouve dans le comité B.

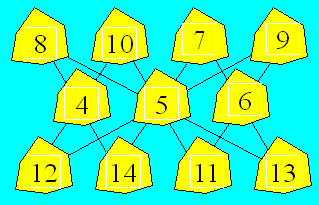
Solution 55. Le nombre de billes par arbre est donné.

Solution 56. 1^e En divisant 10 000 par 26, on obtient 384 reste 16. La 10 000^e lettre correspond à la 16^e lettre de l’alphabet, c’est-à-dire la lettre P.

2^e Pour écrire les nombres de

1 à 9 : 1 × 9 = 9 chiffres

10 à 99 : 2 × 90 = 180 chiffres

100 à 999 : 3 × 900 = 2 700 chiffres

Total:                          2 889 chiffres

Le 10 000^e chiffre se trouve dans un nombre de quatre chiffres, puisqu’il y en a 36 000. Il s’agit de chercher le 7 111^e chiffre à partir de 1 000. En divisant 7 111 par 4, on obtient 1 777 reste 3. Le 10 000^e chiffre est le 3^e chiffre de 1 777, soit 7.

Solution 57. Comme Armande et Carol ont déposé 995 $, Brigitte a déposé 1 245 $ - 995 $ = 250 $. À partir des autres données, on trouve que François a déposé 550 $, Henriette 580 $ et David 280 $. Étienne a donc déposé 415 $. En complétant le tableau, on obtient :

Solution 58. Le nombre de diviseurs est donné en regard de chaque entier entre 9 et 59.

L’allocation de Christian sera de 10 $. Le problème peut être résolu par ordinateur.

Solution 59. Puisque le produit est inférieur à 50 000, C est inférieur à 5. Donc R = 5. C = 1 ou 3. Si C = 3, A = 1 : cela donnerait 48 195. D’où, C = 1. Après des essais où C = 1 et R = 5, on obtient 135 × 351 = 47 385.

Par ailleurs, à cause du dernier chiffre 3, on a le produit de 1 et de 3 ou le produit de 7 et de 9. Compte tenu de la grandeur du produit, N et M valent 7 ou 9. Après des essais, on obtient : 927 × 729 ou 729 ´ 927 = 675 783. ROC devient 521.

Solution 60. 1^e On soustrait 3 de 30 et on divise le résultat par 6. On obtient 4 reste 3. Puisque le reste est 3, on décale de 3 le jour de la semaine. Le 30 mai est un mardi.

2^e Il y a 363 jours du 2 janvier au 29 décembre. En effet, 1984 est une année bissextile. De plus, on ne compte pas le 1^er janvier, ni les 30 et 31 décembre. Or, 363 ÷ 6 = 60 reste 3. Donc, le 29 décembre 1984 est un jeudi.

3^e Voici le jour de la semaine du 5 avril de 1970 à 1978.

C’est en 1978 que l’anniversaire de naissance d’Odette sera à nouveau un jeudi.

Solution 61. Les branches situées à droite contiennent successivement 2, 5, 10, 17 feuilles. La différence entre chaque branche est respectivement de 3, de 5 et de 7 feuilles. Donc, la dernière branche avait 17 + 9 ou 26 feuilles. Les branches situées à gauche ont une feuille de plus lorsque le nombre de feuilles à droite est pair et une feuille de moins lorsque le nombre à droite est impair. La dernière branche à gauche avait 27 feuilles. L’arbre portait 121 feuilles.

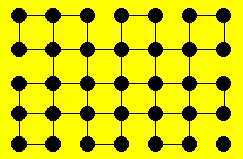
Solution 62. Lucie pourra clôturer 17 parcelles. Voici une façon de disposer le fil :

Solution 63. Le mot de passe est 143. Le problème peut être résolu par ordinateur.

Solution 64. Il y a neuf carrés parfaits qui contiennent cinq chiffres de 1 à 5.

Par ailleurs, 3 025 nombres peuvent être formés. La probabilité est donc de 9 sur 3 025. Comme Martin recouvre 300 fois sa mise, selon toute probabilité il gagnera 2 700 $ quand il en dépensera 3 025 $. Martin perdra 325 $ quand il misera 3 025 $, donc une perte d’environ 11 ¢ par dollar.

Solution 65. Voici le chiffre qui correspond à chaque couleur :

♥ = 2         ♠ =  5            ♣ = 3          ♦ = 8

Solution 66. La division reconstituée est :

Solution 67. Voici le tableau des combinaisons à partir du nombre de chocolats à la fraise :

Michèle peut préparer 84 boîtes différentes. Le problème peut être résolu par ordinateur.

Solution 68. Chaque ensemble de deux cartes constitue un nombre de deux chiffres. La différence entre chaque paire est 13. Les deux dernières cartes sont : le huit de cœur et le sept de carreau.

Solution 69. Les pointillés indiquent la ligne médiane d’un domino. Voici une façon dont les dominos sont disposés :

Solution 70. Faisons des essais en divisant un gâteau successivement par un, deux, trois, quatre, cinq traits. Pour obtenir le plus grand nombre de morceaux, tous les traits, à partir du troisième, doivent rencontrer les traits existants sauf le précédent. Chaque fois qu’on fait un nouveau trait de couteau, le nombre de morceaux augmente du nombre de traits déjà faits.

Le nombre de morceaux sera donc : 2 + (1 + 2 + 3 + … + 19) = 192. Pascal obtiendra 192 morceaux.

Solution 71. Après modification, il y avait 18 perles vraies de rang impair et huit perles vraies de rang pair. Louise enleva quatre perles de rang impair (donc probablement trois vraies) et trois perles de rang pair (donc probablement une vraie). Selon toute probabilité, il reste 22 perles authentiques dans le collier de Louise.

Solution 72. 1^e Pierre et Réjeanne ont respectivement 11 et 16 disques. Ils ont donc ensemble 27 disques.

2^e Paul, Martine et Lucie ont respectivement 8,15 et 17 disques.

Solution 73. Le deuxième nombre parfait est 28. Le problème peut être résolu par ordinateur.

Solution 74. 1^e Un nombre est divisible par 8 si ses trois derniers chiffres forment un nombre divisible par 8. Or 726 ÷ 8 = 90 reste 6. Donc, six dollars ne seront pas distribués quelles que soient les valeurs de A et de M.

2^e Tout nombre de six chiffres formé par deux tranches identiques de trois chiffres est divisible par 7. Tous les livres seront distribués.

3^e Un nombre est divisible par 125 si ses trois derniers chiffres forment un nombre divisible par 125. Or 832 ÷ 125 = 6 reste 82. Donc, 82 cahiers ne seront pas distribués quelles que soient les valeurs de R et de S.

4^e LOT = 8 × MER. D’où LOT + MER = 9 × MER. Donc, toutes les fleurs seront distribuées.

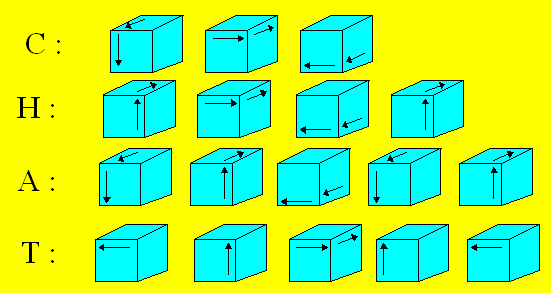
Solution 75. Pour chacune des lettres, vous faites les mouvements indiqués. Vous tenez toujours le cube dans la même position. À la fin, la lettre apparaîtra sur la face que vous avez devant vous. Deux flèches dans un cube permettent un demi-tour ; une seule flèche un quart de tour.

Solution 76. Une triade correspond à 3 ou 3¹. Une viade correspond à 9 ou 3². Une xiade correspond à 27 ou 3³. Une ziade correspond à 81 ou 3⁴. On a donc : (2 × 81) + (1 × 27) + (1 × 3) + 2 = 194. Cet habitant possède 194 chevaux.

Solution 77. L’avoir de Martin est un multiple de 41, c’est-à-dire 41 $, 82 $, 123 $, 164 $, etc.

41 ÷ 6 = 6 reste 5               41 ÷ 7 = 5 reste 6                      41 ÷ 13 = 3 reste 2

Cherchons maintenant le plus petit nombre n tel que :

n ÷ 6 donne 1 comme reste, car 5 × 1 = 5

n ÷ 7 donne 1 comme reste, car 6 × 1 = 6

n ÷ 13 donne 6 comme reste, car 2 × 6 = 12

Pour 6 et 7, n = (6 × 7) + 1 ou 43. Ajoutons successivement 42 et vérifions le reste de la division par 13. On trouvera n = 253. L’avoir de Martin est de 253 × 41 ou 10 373 $.

Solution 78. Utilisons 100 comme premier nombre ; alors le deuxième nombre varie de 101 à 899 : ce qui donne 799 plaques.

Utilisons 101 comme premier nombre ; alors le deuxième nombre varie de 100 à 898 sauf 101 : ce qui donne 798 plaques.

Utilisons 102 comme premier nombre ; alors le deuxième nombre varie de 100 à 897 sauf 102 : ce qui donne 797 plaques. Et ainsi de suite jusqu’à ce que 499 soit le premier nombre : ce qui donne 400 plaques.

Utilisons 500 comme premier nombre ; alors le deuxième nombre varie de 100 à 499 : ce qui donne 400 plaques.

Utilisons 501 comme premier nombre ; alors le deuxième nombre varie de 100 à 498 : ce qui donne 399 plaques. Et ainsi de suite jusqu’à ce que 899 soit le premier nombre : ce qui donne une plaque.

Le nombre total de plaques est donc :

799 + 798 + 797 + … + 400 + 400 + 399 + 398 + … + 1 = 320 000.

Il est possible de fabriquer 320 000 plaques.

Solution 79. Puisqu’il y a le même nombre de personnes par groupe de deux chars et qu’il y a en tout 78 personnes, les combinaisons possibles sont : (1, 12), (2, 11), (3, 10), (4, 9), (5, 8), (6, 7).

Puisque les trois premiers chars et les trois suivants contiennent 19 et 20 personnes, il faut prendre la combinaison (6, 7) pour le troisième et le quatrième char. De la même façon, il faut prendre la combinaison (5, 8) pour le neuvième et le dixième char.

Les numéros restant à attribuer aux autres chars sont 1, 2, 3, 4 et 9, 10, 11, 12. Comme le deuxième char contient plus de personnes que le premier, son numéro est 9. Les numéros des chars sont dans l’ordre : 4, 9, 6, 7, 3, 10, 2, 11, 8, 5, 1, 12.

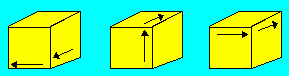
Solution 80. Cette séquence doit être réalisée deux fois de suite.