Ce recueil contient 120 récréations pour lesquelles il faut établir une formule. Une solution détaillée est suggérée pour les problèmes de rang impair. Ceux de rang pair sont un prolongement du problème précédent et la solution n’est pas donnée.

Rappelons qu’une formule mathématique est une égalité dans laquelle le premier membre est constitué par l’inconnue ou la donnée recherchée et dans laquelle le deuxième membre contient des variables sur lesquelles on opère. Par exemple, la formule permettant de déterminer l’aire d’un rectangle est A = B × H, où A est l’aire, B la mesure de la base et H celle de la hauteur. Quand on connaît la base et la hauteur d’un rectangle, on n’a qu’à appliquer cette formule pour trouver l'aire.

Dans ce recueil, à titre d'aide, on suggère que le premier membre soit m qui représente le résultat souhaité. Le deuxième membre est alors constitué de facteurs en n et de constantes. Par exemple, une formule recherchée peut être exprimée ainsi : m = 3n + 7. Dans ce cas, si n = 5, m = 22 ; si n = 6, m = 25, etc. On voit que m varie en fonction de n.

Amusez-vous bien.

1. Distribution de dominos
Des enfants se sont réunis dans la salle de jeux municipale. Il y a là deux filles de plus que de garçons. Chaque garçon donne cinq pièces de dominos à chacune des filles. Chaque fille donne trois pièces à chacun des garçons.

Trouvez une formule qui permet de déterminer la quantité de dominos distribués en fonction d’un nombre donné de garçons présents.

Aide. On pose m la quantité de dominos et n le nombre de garçons présents.

2. Prolongement
Même énoncé que précédemment.

Une quantité de dominos étant donnée, trouvez une formule qui permet de déterminer le maximum d’enfants présents.

3. Des insectes laborieux
Chaque matin, avant d’aller butiner les fleurs des pommiers, la reine de la ruche demande aux abeilles de se placer en rangées. La première rangée contient deux abeilles et chaque rangée successive contient cinq abeilles de plus que la précédente.

Trouvez une formule qui permet de déterminer le nombre d’abeilles dans une rangée donnée.

Aide. On pose m le nombre d’abeilles par rangée et n le rang d’une rangée.

4. Prolongement
Même énoncé que précédemment.

Étant donné un nombre d’abeilles, trouvez une formule qui permet de déterminer le rang de la rangée où la dernière abeille apparaît.

5. Bicyclettes de Thomas
Thomas commence par dessiner neuf bicyclettes en un carré, comme il est montré à gauche. Il ajoute successivement une colonne. Il compte alors le nombre de rangées de trois bicyclettes voisines qu’il est possible de former horizontalement, verticalement et diagonalement. Par exemple, dans chaque ligne de la deuxième figure, on peut compter deux rangées de trois bicyclettes, soit six rangées. En colonnes, on peut compter quatre rangées. En diagonale, on peut aussi compter quatre rangées.

Trouvez une formule qui permet de déterminer le nombre de rangées de trois bicyclettes voisines en fonction d’un nombre de bicyclettes d’une ligne d’une figure donnée.

Aide. On pose m le nombre de rangées de trois bicyclettes voisines et n le nombre de bicyclettes d’une ligne.

6. Prolongement
Même énoncé que précédemment.

Trouvez une formule qui permet de déterminer le nombre de rangées de trois bicyclettes voisines en fonction du nombre de bicyclettes d’une figure donnée.

7. Mois riche en coquillages
Le 1^er juillet, Nicolas a commencé une collection de coquillages. Ce jour-là, il en a recueilli 2. Le lendemain, il en a ajouté 3 à sa collection. Par la suite, le nombre de coquillages a augmenté de 3 à chaque jour.

Trouvez une formule qui permet de déterminer le nombre de coquillages recueillis lors d’un jour quelconque de juillet.

Aide. On pose m le nombre de coquillages et n le quantième du mois de juillet.

8. Prolongement
Même énoncé que précédemment.

Trouvez une formule qui permet de déterminer le nombre de coquillages recueillis depuis le 1^er juillet jusqu’à un quantième donné du mois.

9. Serpent d’Étienne
Étienne écrit les nombres consécutifs à partir de 7 jusqu’à 25 dans la grille ci-après en serpentant. Puis, il continue selon le même modèle.

Trouvez une formule qui permet de déterminer la somme des nombres d’une colonne donnée.

Aide. On pose m la somme des nombres de la colonne donnée et n le rang d’une colonne.

10. Prolongement
Même énoncé que précédemment.

Trouvez une formule qui permet de déterminer le nombre inférieur d’une colonne donnée.

11. Chats de Philomène
Philomène dessine des chats en carrés comme ci-après. Chaque chat est situé à cinq mètres d’un autre en ligne et en colonne. Philomène part du chat du coin supérieur gauche. Elle se dirige vers la droite et va toucher au chat du coin opposé. Sa sœur part du même endroit que Philomène. Elle se dirige vers le bas et va toucher au chat voisin à gauche de celui visité par Philomène.

Trouvez une formule qui permet de déterminer la distance totale parcourue par les deux soeurs en fonction du nombre de chats par rangée de la figure donnée.

Aide. On pose m la distance totale parcourue en mètres et n le nombre de chats par rangée.

12. Prolongement
Même énoncé que précédemment.

Trouvez une formule qui permet de déterminer le nombre total de chats à partir de la première figure jusqu’à une figure donnée, et ceci en fonction du nombre de chats par rangée de la dernière figure.

13. Navets d’Alyssa
Alyssa fait les commandes de légumes pour un marché d’alimentation. Un bon lundi, elle note qu’il lui reste 10 sacs de navets en stock. Cette semaine-là, elle achète 11 sacs et elle en vend 9. La semaine suivante, elle en achète 12 et en vend 10. La semaine d’après, elle en achète 13 et en vend 11. Dans les semaines qui suivent, elle achète toujours un sac de navets de plus que la semaine précédente et elle en vend toujours un de plus.

Trouvez une formule qui permet de déterminer le nombre de navets en stock à la fin d’une semaine donnée.

Aide. On pose m le nombre de navets en stock à la fin d’une semaine et n le rang de la semaine.

14. Prolongement
Même énoncé que précédemment.

Une quantité paire de navets étant donnée, trouvez une formule qui permet de déterminer en quelle semaine cette quantité sera atteinte.

15. Tout en rousseur
Au pays de la Rousseur, les écureuils roux augmentent leur production de trois noisettes par jour. Voici un tableau qui indique le nombre de noisettes recueillies pour les cinq premiers jours :

Trouvez une formule qui permet de déterminer le nombre de noisettes recueillies pendant deux jours consécutifs en fonction du rang donné du premier des deux jours.

Aide. On pose m le nombre de noisettes recueillies pendant deux jours consécutifs et n le rang du premier des deux jours.

16. Prolongement
Même énoncé que précédemment.

Trouvez une formule qui permet de déterminer le nombre total de noisettes recueillies à partir du cinquième jour jusqu’à un jour ultérieur de rang donné.

17. Cure-dents de Flavie
Flavie trace une première colonne de deux hexagones ; la suivante contient un seul hexagone et ainsi de suite en alternance. Voici la figure qui présente les huit premières colonnes :

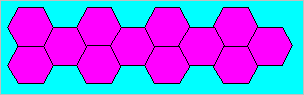
Avec des cure-dents, Flavie décide de reproduire la succession d’hexagones.

Trouvez une formule qui permet de déterminer le nombre de cure-dents requis pour reproduire la figure jusqu’à une colonne donnée de rang impair.

Aide. On pose m le nombre de cure-dents requis et n le rang impair de la colonne.

18. Prolongement
Même énoncé que précédemment.

Trouvez une formule qui permet de déterminer le nombre de cure-dents requis pour reproduire la figure jusqu’à une colonne de rang donné.

19. Pyramide d’Alexandre
Alexandre a préparé le tableau ci-après. Tout nombre appartenant à une ligne supérieure est égal à la somme des deux nombres inférieurs adjacents. Par exemple, 7 + 4 = 11.

Dans un autre tableau de même forme, Alexandre suppose que les quatre nombres de la ligne inférieure sont consécutifs de façon décroissante.

Trouvez une formule qui permet de déterminer le nombre supérieur en fonction du premier nombre donné de la ligne inférieure.

Aide. On pose m le nombre supérieur et n le premier nombre de la ligne inférieure.

20. Prolongement
Même énoncé que précédemment, sauf qu’Alexandre suppose que les nombres de la ligne inférieure appartiennent à la suite 2, 5, 8, 11, 14, 17, ... dans cet ordre.

Trouvez une formule qui permet de déterminer le nombre supérieur en fonction du dernier nombre donné de la ligne inférieure.

21. Impairs de Julia
Julia écrit les entiers consécutifs impairs à partir de 1. Elle insère alternativement entre les nombres les signes + et -. Au fur et à mesure, elle calcule le résultat. Par exemple, elle a écrit :

Trouvez une formule qui permet de déterminer le résultat d’une égalité qui contient un nombre impair d’entiers.

Aide. On pose m le résultat de l’égalité et n le nombre impair d’entiers.

22. Prolongement
Même énoncé que précédemment.

Trouvez une formule qui permet de déterminer le résultat d’une égalité en fonction du dernier entier dans le premier membre.

23. Grilles d’Océanne
Océanne prépare des grilles rectangulaires qui ont deux rangées verticales de plus que de rangées horizontales. Elle veut compter le nombre de grilles 2 × 2 qu’il est possible de trouver dans ces grilles rectangulaires. Par exemple, dans une grille 2 × 4, elle peut dénombrer trois carrés 2 × 2.

Trouvez une formule qui permet de déterminer le nombre de carrés 2 × 2 en fonction du nombre de lignes d’une grille donnée.

Aide. On pose m le nombre de carrés 2 × 2 et n le nombre de lignes.

24. Prolongement
Même énoncé que précédemment.

Trouvez une formule qui permet de déterminer le nombre de carrés de toute grandeur en fonction du nombre de lignes d’une grille rectangulaire donnée.

25. Noisettes de Julia
Julia met d’abord une noisette dans un sac. Par la suite, chacun de ses amis doit déposer sept noisettes. À la suite d’un dépôt, Julia vérifie si les noisettes du sac pourraient être partagées également entre quatre enfants. Dans l’affirmative, elle dessine une étoile.

Trouvez une formule qui permet de déterminer la quantité de noisettes dans le sac quand un nombre donné d’étoiles auront été dessinées.

Aide. On pose m la quantité de noisettes et n le nombre d’étoiles.

26. Prolongement
Même énoncé que précédemment.

Trouvez une formule qui permet de déterminer le nombre d’étoiles qui auront été dessinées lorsqu’une quantité donnée de noisettes aura été atteinte.

27. Suites de Martin
Martin écrit les entiers consécutifs à partir de 1. Par la suite, il forme tous les groupes de deux entiers différents dont la somme est le nombre qui suit le dernier entier écrit. Par exemple, si le dernier nombre est 6, on peut former trois groupes de deux entiers différents dont la somme est 7 : 1 + 6, 2 + 5, 3 + 4.

Trouvez une formule qui, en fonction d’un dernier entier donné de la suite, permet de déterminer le nombre de groupes de deux entiers différents qui peuvent être formés.

Aide. On pose m le nombre de groupes et n le dernier entier de la suite.

28. Prolongement
Martin écrit les entiers consécutifs à partir de 1 comme dans l’énoncé précédent. Par la suite, il forme tous les groupes de trois entiers différents dont la somme est le double du dernier entier écrit.

Trouvez une formule qui, en fonction d’un dernier entier donné de la suite, permet de déterminer le nombre de groupes de trois entiers différents qui peuvent être formés.

29. Perles de Jérémie
Jérémie a un sac de perles. Il donne les deux tiers de ses perles plus une à sa sœur. Puis, il donne les trois quarts des perles qui restent plus une à son frère. Le premier cas où les dons pourront se faire, Jérémie a 15 perles.

Trouvez une formule qui permet de déterminer le nombre de perles du sac dans les cas où il est possible de faire ces dons.

Aide. On pose m le nombre de perles du sac et n le rang du cas possible.

30. Prolongement
Jérémie a un sac de perles. Il donne à sa sœur la moitié de ses perles plus deux. Il donne à son frère le tiers des perles qui restent plus trois. Puis, il donne à un ami le quart de ce qui reste plus quatre.

Trouvez une formule qui permet de déterminer le nombre de perles du sac dans les cas où il est possible de faire ces dons.

31. Visages de Livia
Livia prépare des grilles carrées dans lesquelles elle dessine des visages. Sur toute ligne de rang impair, elle dessine un visage dans la case de gauche. Sur toute ligne de rang pair, elle dessine un visage dans la deuxième case de gauche. Dans les deux cas, elle continue en passant toujours deux cases. Voici un exemple pour les deux premières lignes :

Trouvez une formule qui permet de déterminer le nombre de carrés 3 × 3 qui contiennent trois visages dans une grille carrée donnée.

Aide. On pose m le nombre de carrés 3 × 3 et n le nombre de lignes d’une grille carrée.

32. Prolongement
Même énoncé que précédemment.

Trouvez une formule qui permet de déterminer le nombre de carrés de toute grandeur, sans tenir compte des visages, dans une grille carrée donnée.

33. Carottes de Cédric
Cédric sème des graines de carottes. Il met :

• cinq graines dans une première rangée.

• deux graines de plus dans la deuxième rangée que dans la première.

• trois graines de plus dans la troisième rangée que dans la deuxième.

• quatre graines de plus dans la quatrième rangée que dans la troisième.

• et continue en ajoutant successivement deux, trois, quatre graines.

Trouvez une formule qui permet de déterminer le nombre de graines semées dans n’importe quelle rangée.

Aide. On pose m le nombre de graines et n le rang d’une rangée.

34. Prolongement
Même énoncé que précédemment.

Trouvez une formule qui permet de déterminer le nombre total de graines semées à partir du début jusqu’à une rangée donnée.

35. Tableau d’Alexandra
Alexandra a préparé le tableau ci-après. Elle a écrit les entiers 2, 3, 4 dans la première colonne. Puis, elle a augmenté de 4 d’une colonne à l’autre en ajoutant des colonnes au besoin.

Trouvez une formule qui permet de déterminer l’entier qui apparaît à l’intersection d’une ligne et d’une colonne donnée.

Aide. On pose m l’entier, L le rang d’une ligne et C le rang d’une colonne.

36. Prolongement
Même énoncé que précédemment.

Un nombre étant donné, trouvez une formule qui permet de situer ce nombre dans la grille ou d’affirmer qu’il n’est pas dans la grille.

37. Tuiles de Cédrika
Cédrika prend des tuiles de 1 × 2 centimètres carrés. Elle les place de façon à former le contour d’un carré. Elle continue à former d’autres carrés selon la même régularité.

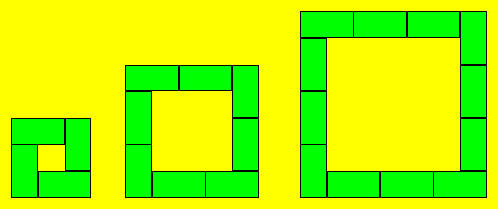
Trouvez une formule qui permet de déterminer l’aire du carré intérieur en fonction du nombre de tuiles d’une figure donnée.

Aide. On pose m l’aire du carré intérieur en centimètres carrés et n le nombre de tuiles d’une figure.

38. Prolongement
Même énoncé que précédemment.

Trouvez une formule qui permet de déterminer le nombre total de tuiles à partir de la première figure jusqu’à une figure de rang donné.

39. Fleurs de Marcelle
Le 1^er octobre, Marcelle décide de dessiner des fleurs dans son journal. Ce jour-là, elle en dessine cinq. Le lendemain, elle en dessine deux de plus. Par la suite, elle dessine deux fleurs de plus chaque jour.

Trouvez une formule qui permet de déterminer le nombre de fleurs dessinées depuis le début du mois jusqu’à la fin d’un jour quelconque.

Aide. On pose m le nombre de fleurs et n le quantième du mois d’octobre.

40. Prolongement
Même énoncé que précédemment.

Trouvez une formule qui permet de déterminer en quel quantième d’octobre un nombre donné de fleurs a été atteint.

41. Fête de fourmis
Un certain nombre de fourmis participent à la fête annuelle des récoltes. Chaque fourmi a l’obligation de donner un pain à chacune des autres fourmis présentes.

Trouvez une formule qui permet de déterminer la quantité de pains distribués en fonction d’un nombre quelconque de participantes.

Aide. On pose m le nombre de pains distribués et n le nombre de fourmis.

42. Prolongement
Même énoncé que précédemment.

Trouvez une formule qui permet de déterminer le nombre maximum de participantes en fonction d’un nombre donné de pains.

43. Grille de Sophia
Sophia écrit les nombres impairs consécutifs dans une grille comportant sept colonnes et autant de lignes que nécessaires.

Trouvez une formule qui permet de déterminer le rang de la ligne où apparaît un nombre impair quelconque.

Aide. On pose m le rang de la ligne et n un nombre impair.

44. Prolongement
Même énoncé que précédemment.

Trouvez une formule qui permet de déterminer le rang de la colonne où apparaît un nombre impair quelconque.

45. Clôtures de Raoul
Raoul plante des piquets et place des tiges de façon à rejoindre les piquets deux à deux ou plus quand les piquets sont en ligne droite. Il a d'abord mis deux colonnes de deux piquets. Ensuite, il a mis trois colonnes de deux piquets. Il continue ainsi en ajoutant une colonne de deux piquets vers la droite d’une figure à l’autre.

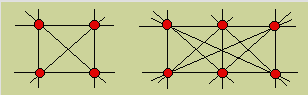
Trouvez une formule qui permet de déterminer le nombre de tiges en fonction du nombre de colonnes de piquets d’une figure donnée.

Aide. On pose m le nombre de tiges et n le nombre de colonnes.

46. Prolongement
Même énoncé que précédemment.

Trouvez une formule qui permet de déterminer le nombre total de tiges à partir de la figure formée de deux colonnes jusqu’à une figure donnée.

47. Cadenas de Régis
Régis dessine trois cadenas en une première rangée horizontale. Par la suite, il augmente d’un cadenas à chaque rangée.

Trouvez une formule qui permet de déterminer le nombre total de cadenas à partir de la première rangée jusqu’à une rangée donnée.

Aide. On pose m le total des cadenas et n le rang d’une rangée horizontale.

48. Prolongement
Même énoncé que précédemment.

Un nombre de cadenas étant donné, trouvez une formule qui permet de déterminer le rang de la rangée où on peut trouver le dernier cadenas correspondant à ce nombre.

49. Alphabet d’Ariane
Ariane écrit les lettres de l’alphabet selon le modèle ci-après. Elle écrit A une fois, B trois fois, C cinq fois, D sept fois et ainsi de suite. Elle veut connaître le rang, dans la séquence, de la première lettre de chaque groupe de lettres identiques. Par exemple, A est au premier rang, le premier B est au deuxième rang, le premier C est au cinquième rang dans la séquence.

Trouvez une formule qui permet de déterminer le rang de la première lettre d’un groupe quelconque de lettres identiques et ce, en fonction de son rang dans l’alphabet.

Aide. On pose m le rang de la première lettre d’un groupe et n le rang de la lettre dans l’alphabet.

50. Prolongement
Même énoncé que précédemment.

Un rang étant donné dans la séquence, trouvez une formule qui permet de déterminer la lettre qui apparaît à ce rang.

51. Dominos de Sylvain
Sylvain dessine des grilles rectangulaires qui ont une rangée verticale de plus que de rangées horizontales. Il y place des dominos tels que chaque pièce recouvre deux cases. Il veut les disposer de façon à occuper le plus de cases possible.

Trouvez une formule qui permet de déterminer le nombre de dominos en fonction d’un nombre donné de rangées horizontales d’une grille.

Aide. On pose m le nombre de dominos et n le nombre de rangées horizontales.

52. Prolongement
Même énoncé que précédemment.

Un nombre de dominos étant donné, trouvez une formule qui permet de déterminer la grandeur de la grille qui permet de placer le plus de pièces possible.

53. Médaillons d’Isabelle
Le 1^er janvier, Isabelle a commencé une collection de médaillons. Ce jour-là, elle en a reçu 2. Le lendemain, elle en a ajouté 5 à sa collection. Par la suite, le nombre de médaillons a augmenté de 3 d’un jour à l’autre.

Trouvez une formule qui permet de déterminer, en n’importe quel jour de janvier, le nombre total de médaillons obtenus depuis le début du mois.

Aide. On pose m le nombre total de médaillons obtenus depuis le début du mois et n le quantième du mois de janvier.

54. Prolongement
Même énoncé que précédemment.

Un nombre de médaillons inférieur à 1400 étant donné, trouvez une formule qui permet de déterminer en quel jour de janvier ce nombre aura été atteint ou aura été dépassé avant le jour suivant.

55. Grille de Mathis
Mathis a préparé la grille ci-après. Il désire la compléter en ajoutant des lignes et en écrivant les nombres selon la même régularité.

Trouvez une formule qui permet de déterminer le nombre qui devra apparaître sur une ligne et dans une colonne donnée.

Aide. On pose m le nombre de la grille, L le rang de la ligne et C le rang de la colonne.

56. Prolongement
Même énoncé que précédemment.

Un nombre étant donné, trouvez une formule qui permet de savoir si ce nombre peut apparaître dans la grille et, dans l’affirmative, de déterminer sa position.

57. Polygones de Micheline
Micheline représente successivement par des points les sommets d’un triangle, d’un quadrilatère, d’un pentagone, d’un hexagone, etc. Elle joint chaque point à tout autre point par des droites.

Trouvez une formule qui permet de déterminer le nombre de droites obtenues en fonction du nombre de côtés d’un polygone quelconque.

Aide. On pose m le nombre de droites et n le nombre de côtés du polygone.

58. Prolongement
Même énoncé que précédemment.

Un nombre de droites étant donné, trouvez une formule qui permet de déterminer le nombre de côtés du polygone où ce nombre a été atteint.

59. Vers le trésor
Pour accéder à un trésor caché sur une montagne, on a construit une séquence d’escaliers. Le premier escalier a trois marches. Chacun des escaliers suivants a quatre marches de plus que le précédent.

Trouvez une formule qui permet de déterminer le nombre de marches foulées à partir du premier escalier jusqu’à la dernière marche d’un escalier de rang donné.

Aide. On pose m le nombre de marches foulées et n le rang de la dernière marche de l’escalier de rang donné.

60. Prolongement
Même énoncé que précédemment.

Trouvez une formule qui permet de déterminer le nombre de marches foulées à partir du premier escalier jusqu’à la première marche d’un escalier de rang donné.