61. Croix de Sylvain
Sylvain dessine des grilles rectangulaires qui ont une rangée de cases verticales de plus que de cases horizontales. Il veut y colorier des croix qui occupent des positions différentes. Par exemple, dans une grille 3 × 4, on peut disposer deux croix dans les positions différentes illustrées.

Trouvez une formule qui permet de déterminer le nombre de croix qu’il est possible de colorier dans une grille rectangulaire donnée.

Aide. On pose m le nombre de croix et n le nombre de lignes de la grille.

62. Prolongement
Même énoncé que précédemment.

Un nombre de croix étant donné, trouvez une formule qui permet de déterminer la grandeur maximale de la grille dans laquelle ces croix pourront être coloriées.

63. Histoire de pommes
A cueille 4 pommes, B en cueille 3 de plus que A, C en cueille 3 de plus que B, D en cueille 3 de plus que C et ainsi de suite selon la même régularité en faisant intervenir E, F, G, etc.

Trouvez une formule qui permet de déterminer le nombre de pommes cueillies par un groupe donné de trois personnes voisines en ordre alphabétique, et ce en fonction du rang de la personne centrale du groupe.

Aide. On pose m le nombre de pommes cueillies par un groupe de trois personnes voisines et n le rang de la personne centrale du groupe.

64. Prolongement
A cueille 2 pommes, B en cueille 3 de plus que A, C en cueille 4 de plus que B, D en cueille 5 de plus que C, E en cueille 6 de plus que D et ainsi de suite selon la même régularité.

Trouvez une formule qui permet de déterminer le nombre de pommes cueillies par un groupe donné de trois personnes voisines en ordre alphabétique, et ce en fonction du rang de la personne centrale du groupe.

65. Triangles d’Éloi
Éloi dessine des triangles équilatéraux. Dans le premier, il trace une parallèle et trois perpendiculaires à la base. Dans le deuxième, il trace deux parallèles et cinq perpendiculaires à la base. Dans le troisième, il trace trois parallèles et sept perpendiculaires à la base. Il continue selon la même régularité. Voici le tracé des trois premières figures :

Éloi s’amuse à compter les triangles de toute grandeur dans chaque figure, en incluant le grand triangle. Par exemple, dans la première figure, on peut compter huit triangles.

Trouvez une formule qui permet de déterminer le nombre de triangles de toute grandeur en fonction du nombre de parallèles à la base d’une figure donnée.

Aide. On pose m le nombre de triangles et n le nombre de parallèles à la base.

66. Prolongement
Même énoncé que précédemment.

Trouvez une formule qui permet de déterminer le nombre de triangles de toute grandeur en fonction du nombre de perpendiculaires à la base d’une figure donnée.

67. Catherine additionne
Catherine choisit un entier. Elle fait la somme des trois résultats suivants :

= l’entier élevé au carré.

= l'entier qui suit élevé au carré.

= le produit des deux premiers résultats.

Puis, elle extrait la racine carrée de la somme. Par exemple, si elle choisit 5 comme entier. La somme sera 25 + 36 + 900 = 961. Le résultat final sera 31.

Trouvez une formule qui permet de déterminer le résultat final en fonction d’un entier quelconque.

Aide. On pose m le résultat final et n un entier.

68. Prolongement
Même énoncé que précédemment, sauf que Catherine choisit seulement les multiples de 3.

Trouvez une formule qui permet de déterminer le résultat final en fonction du rang de n’importe quel multiple de 3.

69. Allumettes de Lili
Lili représente des grilles carrées avec des allumettes. Voici un exemple d’une grille 3 × 3 :

Trouvez une formule qui permet de déterminer le nombre d’allumettes requises pour former une grille carrée d’une grandeur donnée.

Aide. On pose m le nombre d’allumettes et n le nombre de cases par ligne ou par colonne.

70. Prolongement
Même énoncé que précédemment.

Trouvez une formule qui permet de déterminer le nombre d’allumettes requises pour former une grille rectangulaire dont le nombre de colonnes est supérieur de 2 au nombre de lignes.

71. Triangle d’Isaac
Isaac dispose les entiers consécutifs à partir de 5 en un triangle comme ci-après. Puis, il continue en plaçant un nombre de plus d’une ligne à l’autre.

Trouvez une formule qui permet de déterminer la somme des deux nombres du milieu d’une ligne donnée de rang pair.

Aide. On pose m la somme des deux nombres du milieu et n le rang d’une ligne de rang pair.

72. Prolongement
Même énoncé que précédemment.

Trouvez une formule qui permet de déterminer la somme du premier et du troisième nombre d’une ligne donnée.

73. Autobus d’Henri
Henri dessine des autobus selon une certaine régularité. Voici les trois premières figures qu’il a formées :

Trouvez une formule qui permet de déterminer le nombre d’autobus pour une figure de rang donné.

Aide. On pose m le nombre d’autobus et n le rang de la figure.

74. Prolongement
Même énoncé que précédemment.

Trouvez une formule qui permet de déterminer le nombre total d’autobus à partir de la première figure jusqu’à une figure de rang donné.

75. Étoiles de Francis
Francis a préparé plusieurs tableaux d’étoiles qui contiennent chacun trois rangées horizontales. D’un tableau à l’autre, il ajoute une colonne d’étoiles. Les trois premiers tableaux sont donnés ci-après. Une araignée part du coin supérieur gauche de chaque tableau. Elle se déplace toujours en avançant de gauche à droite et de haut en bas. Elle s’arrête au coin inférieur droit.

Trouvez une formule qui permet de déterminer le nombre de chemins parcourus par l’araignée en fonction du nombre de colonnes du tableau donné.

Aide. On pose m le nombre de chemins parcourus et n le nombre de colonnes du tableau.

76. Prolongement
Même énoncé que précédemment sauf qu’on forme successivement un carré de 4, 9, 16, 25, ... étoiles.

Trouvez une formule qui permet de déterminer le nombre de chemins parcourus par une araignée en fonction du nombre de lignes ou de colonnes du carré donné.

77. Tableau d’Émile
Émile écrit les nombres à partir de 1 comme ci-après. Il divise chacun des nombres par 7 et note le reste de chaque opération.

Trouvez une formule qui permet de déterminer la somme de tous les restes à partir du début jusqu’à un nombre donné.

Aide. On pose m la somme de tous les restes à partir du début, n le nombre donné, q la partie entière du quotient et r le reste de la division.

78. Prolongement
Émile écrit les nombres impairs à partir de 1. Il divise chacun des nombres par 10 et note le reste de chaque opération.

Trouvez une formule qui permet de déterminer la somme de tous les restes à partir du début jusqu’à un nombre donné.

79. Triangles de Vincent
Vincent dessine des triangles rectangles dont le premier côté de l’angle droit mesure successivement 3, 5, 7, 9, 11, ... centimètres. L’autre côté de l’angle droit mesure 4, 12, 24, 40, 60, ... centimètres.

Trouvez une formule qui permet de déterminer la mesure du deuxième côté de l’angle droit en fonction de la mesure du premier côté.

Aide. On pose m la mesure du deuxième côté de l’angle droit et n la mesure du premier côté.

80. Prolongement
Même énoncé que précédemment.

Trouvez une formule qui permet de déterminer la mesure de l’hypoténuse en fonction de la mesure du premier côté de l’angle droit.

81. Piste de Nicolas
Nicolas a construit une piste de course dans la cour de ses parents. Le long de la piste, il plante des petits drapeaux indiquant la distance depuis le début. Sur le premier drapeau, il inscrit A-7, ce qui correspond à 7 centimètres. Sur le second drapeau, il inscrit B-13. Sur le troisième, il inscrit C-21. Sur le quatrième, il inscrit D-31. Sur le cinquième, il inscrit E-43. Il continue selon la même régularité.

Trouvez une formule qui permet de déterminer la longueur en centimètres de la piste depuis le début jusqu’à une lettre donnée de l’alphabet.

Aide. On pose m la longueur en centimètres et n le rang de la lettre dans l’alphabet.

82. Prolongement
Même énoncé que précédemment.

Étant donné une longueur en centimètres, trouvez une formule qui permet de déterminer la position d’un mobile sur la piste.

83. Pyramides d’Étienne
Étienne découpe des hexagones de même grandeur. Il les assemble en forme de pyramides ayant successivement 1, 2, 3, 4, 5, ... hexagones à la base. Voici un exemple où la base contient quatre hexagones :

Étienne veut maintenant reproduire la pyramide avec des cure-dents.

Trouvez une formule qui permet de déterminer le nombre de cure-dents requis en fonction du nombre d’hexagones à la base.

Aide. On pose m le nombre de cure-dents requis et n le nombre d’hexagones à la base.

84. Prolongement
Même énoncé que précédemment.

Trouvez une formule qui permet de déterminer le nombre de cure-dents requis en fonction du nombre d’hexagones de la pyramide.

85. Points d’Alexia
Alexia dessine successivement des carrés de 9, 16, 25, 36, ... points. Elle veut tracer des losanges dont les sommets ont quatre points.

Trouvez une formule qui permet de déterminer le nombre de losanges dans une grille donnée et ce, en fonction du nombre de lignes ou de colonnes de la grille.

Aide. On pose m le nombre de losanges et n le nombre de lignes ou de colonnes de la grille.

86. Prolongement
Même énoncé que précédemment.

Trouvez une formule qui permet de déterminer le nombre de losanges de toute grandeur d’une grille donnée, et ce en fonction du nombre de lignes ou de colonnes de la grille.

87. Boules de Laurent
Laurent dessine quatre figures de boules comme ci-après. Il continue à dessiner d’autres figures selon le même modèle.

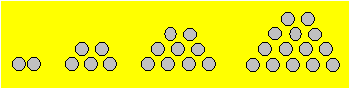
Trouvez une formule qui permet de déterminer le nombre de boules de n’importe quelle figure et ce, en fonction du nombre de boules à la base.

Aide. On pose m le nombre de boules d’une figure et n le nombre de boules à la base.

88. Prolongement
Même énoncé que précédemment.

Un nombre de boules étant donné, trouvez une formule qui permet de déterminer dans quelle figure la dernière boule pourra être posée.

89. Étoiles d’Amélie
À l’école, Amélie a gagné une étoile la première semaine, trois étoiles la deuxième semaine, cinq étoiles la troisième semaine et ainsi de suite en obtenant deux étoiles de plus d’une semaine à l’autre. Elle a écrit ses gains dans le tableau suivant.

Trouvez une formule qui permet de déterminer tous les nombres qui apparaissent sur une ligne donnée.

Aide. On pose m le nombre au début de la ligne donnée et n le rang de la ligne.

90. Prolongement
Même énoncé que précédemment.

Un nombre impair étant donné, trouvez une formule qui permet de déterminer dans quelle rangée horizontale se trouve ce nombre.

91. Citrons de Rébecca
Rébecca dispose des citrons pour former les quatre figures ci-après. Elle continue à former d’autres figures selon la même régularité.

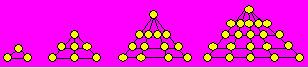
Trouvez une formule qui permet de déterminer le nombre de citrons nécessaires pour former une figure d’un rang donné.

Aide. On pose m le nombre de citrons nécessaires et n le rang de la figure.

Même énoncé que précédemment.

Un nombre de citrons étant donné, trouvez une formule qui permet de déterminer dans quelle figure on pourra poser le dernier citron.

93. Pairs de Lisa
Lisa fait la somme des nombres pairs consécutifs. Elle a écrit :

Trouvez une formule qui permet de déterminer la somme en fonction du plus grand entier du premier membre donné d’une égalité.

Aide. On pose m la somme et n le plus grand entier.

94. Prolongement
Même énoncé que précédemment.

Un nombre pair étant donné, trouvez une formule qui permet de déterminer si ce nombre peut être une somme.

95. Bâtonnets d’Ariane
Ariane dessine des grilles carrées avec des bâtonnets. Sur le contour, elle place des bâtonnets rouges et à l’intérieur des bleus. Voici un exemple :

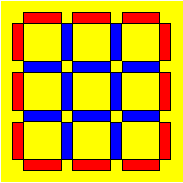
Trouvez une formule qui permet de déterminer le nombre de bâtonnets bleus dans une grille carrée donnée et ce, en fonction du nombre de bâtonnets rouges par côté de la grille.

Aide. On pose m le nombre de bâtonnets bleus et n le nombre de bâtonnets rouges par côté de la grille.

Trouvez une formule qui permet de déterminer le nombre de bâtonnets bleus dans une grille rectangulaire donnée en fonction du nombre de bâtonnets rouges sur le contour.

97. Lettres de Nathaniel
Nathaniel prépare un tableau dans lequel il écrit les lettres de A à N. Il continue ainsi jusqu’à Z ; puis après Z, il écrit A, B, C, et ainsi de suite. D’une ligne à l’autre, il place une lettre de plus.

Trouvez une formule qui permet de déterminer la dernière lettre qui apparaît sur une ligne donnée.

Aide. On pose m le rang en ordre alphabétique de la dernière lettre de la ligne et n le rang d’une ligne.

98. Prolongement
Même énoncé que précédemment.

Trouvez une formule qui permet de déterminer sur quelles lignes la lettre Z apparaîtra.

99. Migration des oies blanches
Chaque printemps, les oies blanches migrent vers le nord. Un bon jour, elles ont formé les quatre groupes suivants. Les autres groupes vers la droite se forment selon la même régularité.

Trouvez une formule qui permet de déterminer le nombre d’oies en fonction du rang d’un groupe donné.

Aide. On pose m le nombre d’oies et n le rang d’un groupe donné.

100. Prolongement
Même énoncé que précédemment.

Un nombre d’oies étant donné, trouvez une formule qui permet de déterminer dans quel groupe sera la dernière oie correspondant à ce nombre.

101. Tableau de Victoria
Victoria a préparé le tableau suivant dans lequel les nombres de la première ligne augmentent de 4 et ceux de la deuxième ligne de 1. Puis, elle prolonge le tableau vers la droite. Elle fait le produit des deux nombres de chaque colonne. Par exemple, le produit pour la septième colonne est 348.

Trouvez une formule qui permet de déterminer le produit des deux nombres d’une colonne donnée.

Aide. On pose m le produit des deux nombres et n le rang de la colonne.

102. Prolongement
Même énoncé que précédemment.

Un nombre étant donné, trouvez une formule qui permet de déterminer si ce nombre peut être le produit des nombres d’une colonne.

103. Carrés de points
Émile représente successivement des carrés par des points sur le contour. Il commence par un carré dont chaque côté a trois points ; puis il continue en augmentant d’un point par côté pour chaque carré successif accolé. Voici la représentation des quatre premiers carrés :

Trouvez une formule qui permet de déterminer le nombre total de points requis quand un carré quelconque a été représenté et ce, en fonction du nombre de points par côté de ce carré.

Aide. On pose m le nombre de points requis et n le nombre de points par côté du dernier carré.

104. Prolongement
Même énoncé que précédemment.

Trouvez une formule qui permet de déterminer le nombre total de points requis quand un carré quelconque a été représenté et ce, en fonction du nombre total de points de ce carré.

105. Pamplemousses d’Octavie
Octavie a acheté quatre pamplemousses. Le même jour, elle en donne deux. Le jour suivant, elle en achète trois. Par la suite, successivement, elle donne deux pamplemousses un jour et en achète trois le jour suivant.

Trouvez une formule qui permet de déterminer le nombre de pamplemousses possédés par Octavie à la fin d’un jour de rang donné.

Aide. On pose m le nombre de pamplemousses possédés par Octavie à la fin d’un jour et n le rang du jour.

106. Prolongement
Même énoncé que précédemment.

Un nombre de pamplemousses étant donné, trouvez une formule qui permet de déterminer en quel jour ce nombre a été atteint pour la première fois.

107. Monnaie de Jessica
Jessica a disposé des pièces de monnaie comme dans les deux figures ci-après. Dans la première figure, il y a deux pièces sur chaque côté des triangles et sur chaque côté du carré. Dans la seconde figure, il y a trois pièces sur chaque côté des triangles et sur chaque côté du carré. Jessica dessine d’autres figures en augmentant d’une pièce par côté.

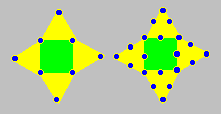
Trouvez une formule qui permet de déterminer le nombre de pièces de monnaie requises pour former une figure de rang donné et ce, en fonction du nombre de pièces par côté des triangles ou du carré.

Aide. On pose m le nombre de pièces de monnaie requises et n le nombre de pièces par côté des triangles ou du carré.

108. Prolongement
Même énoncé que précédemment.

Trouvez une formule qui permet de déterminer le nombre total de pièces de monnaie requises à partir de la première figure jusqu’à une figure dont le nombre de pièces par côté des triangles ou du carré est donné.

109. Œufs de Maxime
Lors de la fête de Pâques de l’an 2004, Maxime a reçu trois œufs en chocolat. Il avait alors quatre ans. À chaque fête de Pâques suivante, il a reçu deux œufs de plus que l’année précédente.

Trouvez une formule qui permet de déterminer le nombre total d’œufs reçus à partir de 2004 jusqu’à une année donnée.

Aide. On pose m le nombre total d’œufs reçus et n l’année donnée. Pour simplifier les calculs, on peut aussi poser a l’âge de Maxime.

110. Prolongement
Même énoncé que précédemment.

Un nombre d’œufs étant donné, trouvez une formule qui permet de déterminer l’âge de Maxime quand il aura atteint ce nombre ou quand il l’aura dépassé sans atteindre le nombre d’œufs de l’année suivante.

111. Triangles de Victor
Victor prépare les quatre figures ci-après. Il dessine d’autres figures selon la même régularité. Il veut connaître le nombre de triangles de toute grandeur dans chaque figure en excluant les triangles d’une seule partie et les triangles dont la base est renversée. Par exemple, dans la troisième figure, Victor peut compter six triangles de quatre parties, trois triangles de neuf parties et le grand triangle.

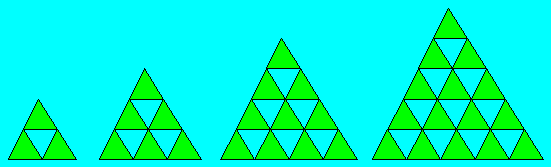
Trouvez une formule qui permet de déterminer, à l’exemple de Victor, le nombre de triangles de toute grandeur et ce, en fonction du rang de la figure.

Aide. On pose m le nombre de triangles de toute grandeur et n le rang de la figure.

112. Prolongement
Même énoncé que précédemment.

Trouvez une formule qui permet de déterminer le nombre de triangles de toute grandeur dont la base est renversée et ce, en fonction du rang de la figure.

113. Lettres de Christophe
Christophe prépare quatre triangles de lettres. Il continue de former d’autres triangles selon la même régularité. Son intention est de compter, dans les figures successives, le nombre de fois qu’on peut lire AB, ABC, ABCD, ABCDE, ... en joignant les lettres voisines de haut en bas.

Trouvez une formule qui permet de déterminer le nombre de fois qu’on peut lire la même expression dans un triangle donné et ce, en fonction du nombre de lettres de la dernière ligne.

Aide. On pose m le nombre de fois et n le nombre de lettres de la dernière ligne.

114. Prolongement
Même énoncé que précédemment.

Trouvez une formule qui permet de déterminer le nombre de fois qu’on peut lire la même expression dans un triangle donné et ce, en fonction du nombre de lettres de la figure.

115. Grilles de Fernando
Fernando prépare des grilles carrées. Il veut compter le nombre de rectangles 2 × 3 qu’il est possible de tracer dans ces grilles. Par exemple, dans une grille 4 × 4, il peut dénombrer 12 rectangles 2 × 3.

Trouvez une formule qui permet de déterminer le nombre de rectangles 2 × 3 dans n’importe quelle grille carrée.

Aide. On pose m le nombre de rectangles 2 × 3 et n nombre de lignes ou de colonnes de la grille.

116. Prolongement
Même énoncé que précédemment.

Trouvez une formule qui permet de déterminer le nombre de rectangles 3 × 4 dans n’importe quelle grille carrée.

117. Rondelles de Mathieu
Mathis assemble des rondelles de façon à obtenir les quatre figures ci-après. La base contient successivement 1, 2, 3 et 4 rondelles.

Trouvez une formule qui permet de déterminer le nombre de rondelles dans une figure dont le nombre de rondelles à la base est donnée.

Aide. On pose m le nombre de rondelles d’une figure et n le nombre de rondelles à la base.

118. Prolongement
Même énoncé que précédemment.

Un nombre de rondelles étant donné, trouvez une formule qui permet de déterminer dans quelle figure la dernière rondelle pourra être posée.

119. Téléphones de Nicolas
Nicolas dessine des téléphones en triangles comme ci-après. Il continue selon la même régularité. Puis, dans chaque rangée horizontale, il marque d’un X chaque téléphone de rang pair.

Trouvez une formule qui permet de déterminer le nombre de X dans un triangle dont le nombre de téléphones à la base est donné.

Aide. On pose m le nombre de X dans le triangle et n le nombre de téléphones à la base.

120. Prolongement
Même énoncé que précédemment.

Un nombre de X étant donné, trouvez une formule qui permet de déterminer dans quel triangle le dernier X pourra être posé.