*******************
Récréations
51 à 100
*******************
51. Carrés et magie
Dans tout carré magique d’ordre 3, la
somme des carrés des éléments de la première ligne est égale à la
somme des carrés des éléments de la troisième ligne. Cela est vrai aussi
pour la somme des éléments de la première et de la troisième colonne. À
partir d’un carré magique d’ordre 3, il est possible de résoudre le
système d’équations suivant :
A + B + C = D + E
+ F
A2 + B2
+ C2 = D2 + E2 + F2
Montrez qu’un carré magique d’ordre
3 ne donne pas toutes les solutions entières du système d’équations.
52. Cubes de Léonard
Léonard élève 5 au cube et divise le
résultat par 9. Le reste est 8. Il fait de même avec 8, 11 et 14. Le reste
est toujours 8. Il écrit cette suite :
5, 8, 11, 14, 17, 20, ...
Montrez que, si on divise par 9 le
cube de chaque terme de cette suite, le reste est 8.
53. Mine d’un mage
MINE de rien, un MAGE SEMA. Chaque lettre
représente un chiffre différent.
|
S E M A
-
M
A G E
M I N E |
Montrez que E ne peut pas être
égal à 3.
54. Deux classes
Les
triangulaires appartiennent à la suite : 1, 3, 6, 10, 15, 21, 28, ... L’exposant
est D, si bien qu’on peut écrire : 1D
= 1, 2D
= 3, 3D
= 6, 4D
= 10, 5D
= 15, etc. Les carrés appartiennent à la suite 1, 4, 9, 16, 25, 36, 49, etc. L’exposant
est 2, si bien qu’on peut écrire : 12
= 1, 22 = 4, 32
= 9, 42 = 16, 52
= 25, etc. Il existe une égalité qui met en relation ces deux classes de
nombres : 32 + 42
= 4D
+ 5D.
Cette égalité peut se traduire par cette proposition : Soit deux carrés
successifs A2 et B2 et deux triangulaires successifs BD
et CD, alors A2 + B2 = BD
+ CD.
Montrez que, dans l’ensemble des entiers positifs, cette
égalité est vraie pour un seul cas : 32
+ 42 = 4D
+ 5D.
55. Treillis de
Jeanne
Jeanne a écrit chacun des nombres de 1 à 8
dans ce treillis de telle manière que la somme dans chaque rangée de trois
cercles reliés par une droite est 13.
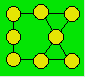
Montrez que, s’il existe au moins
une configuration où la somme est 13 dans chaque rangée, il en existe au
moins une où la somme est 14.
56. Impairs d’Émile
Émile a écrit les premiers termes de la
suite des nombres impairs en un triangle comme ci-après. Sur chaque ligne,
on doit trouver successivement 1, 2, 3, 4, 5, ... termes.
|
1
3 5
7 9
11
13 15
17 19
21
23 25 27 29
..................................... |
Montrez que la somme des nombres de
chaque ligne est un cube.
57. Couples de Gabriel
Gabriel choisit deux nombres entiers. Il les
additionne. Il les soustrait l’un de l’autre. Il les multiplie et les
divise. À la fin, il additionne ces quatre résultats. Par exemple, il
choisit le couple (15, 60). Il fait : 60 + 15 = 75, 60 - 15 = 45, 60 ×
15 = 900 et 60 ÷ 15 = 4. La somme des résultats est 1024.
Montrez qu’il existe exactement
trois couples de nombres entiers sur lesquels on peut opérer pour que la
somme des résultats soit 675.
58. Jetons de Tristan
Dans cette figure, Tristan dispose chacun
des jetons de 1 à 8 pour que la somme soit 15 dans chacune des quatre
rangées de trois cercles reliés par une droite.
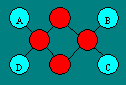
Montrez que A + B + C + D = 12.
59. Urne de Ludovic
Ludovic numérote 99 boules de 1 à 99. Il
les met dans une urne. Au hasard, il prend trois boules à la fois et les
remet dans l’urne.
Montrez que la somme des numéros
des boules sera un multiple de 3 deux fois sur cinq.
60. Quel zig !
Si le nez hume le gaz au rez-de-chaussée, c’est
le temps de sortir, selon un zig inconnu. Dans l’addition suivante, chaque
lettre représente un chiffre différent.
|
N E Z
+ G A Z
R E Z
Z I G |
Montrez que la plus petite valeur de
Z est 7.
61. Dominos de Pascal
Pascal tire de sa boîte huit dominos :
(1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 3), (3, 4), (5, 6). Il veut
faire une chaîne circulaire de dominos telle que deux demi-dominos
adjacents ont le même nombre de points.
Montrez qu’il est impossible de
réaliser une chaîne circulaire avec ces huit dominos.
62. Double de Carmen
Carmen a composé le carré magique d’ordre
3 ci-après. La densité ou somme des nombres dans chaque rangée
horizontale, verticale et diagonale est 42. Le médian est 14. La somme des
éléments extrêmes d’une rangée qui passe par le centre est 28.
|
16 |
9 |
17 |
|
15 |
14 |
13 |
|
11 |
19 |
12 |
Montrez que, dans tout carré
magique d’ordre 3, la somme des éléments extrêmes d’une rangée qui
passe par le centre est le double du médian.
63. Triangle de Simon
Simon a écrit les premiers termes de la
suite des entiers en un triangle comme ci-après. Sur chaque ligne, on doit
trouver successivement 1, 3, 5, 7, 9, ... termes.
|
1
2 3 4
5 6 7 8 9
10 11 12 13 14 15 16
17 18 19 20
21 22 23 24 25
................................................ |
Montrez que la somme des nombres
de chaque ligne est un nombre impair.
64. Sommets d’Anselme
Anselme a formé la figure suivante dans
les cases de laquelle il veut écrire chacun des nombres de 1 à 6. À l’intérieur
de trois triangles, la somme des trois sommets de chaque petit triangle
est indiquée.
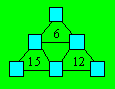
Montrez qu’il est impossible
de disposer les nombres de 1 à 6 dans cette figure.
65.
Ciel d’Alice
Alice a écrit l’addition ci-après.
Elle dit à son amie :
- Tu vois
ce que j’ai écrit. Il te faut attribuer un chiffre à chaque lettre
différente pour que l’addition soit vraie. Par exemple, tu pourrais
trouver : 649 + 2508 = 3157. Toutefois, j’aimerais que tu n’utilises
pas le zéro.
Au bout de plusieurs minutes, l’amie
n’a pas trouvé de réponse. Frustrée, elle affirme qu’aucune
solution n’existe.
Montrez que l’amie a raison.
66. Escaliers de Paule
Paule a agencé des cubes pour faire des
escaliers de 1, 2, 3 et 4 marches. Elle a utilisé respectivement 1, 3,
6 et 10 cubes. Elle dessine d'autres escaliers à la suite sur le même
modèle.
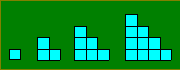
Montrez que la quantité de
cubes nécessaires pour construire deux escaliers voisins est un carré.
67. Premiers de classe
On peut partager tous les entiers en six
classes qui prennent la forme 6n, 6n + 1, 6n + 2, 6n
+ 3, 6n + 4 ou 6n + 5.
Montrez que seuls les nombres de
la forme (6n + 1) ou (6n + 5) peuvent être des nombres
premiers.
68.
Visages d’Amélie
Amélie a dessiné des visages, soit un
carré de 16 et un autre de 25 visages. Elle dit à un ex ami qui l’a
provoquée :
-
Voilà ce que tu es, un homme aux 41 visages.
- Et toi
Amélie, tu es une femme aux 999 visages.

En fait, l’ex s’est trompé.
Il pensait que 999 pouvait être la somme de deux carrés comme 41
; mais ce n’est pas le cas.
Montrez que 999 ne peut pas
être la somme de deux carrés.
69. Somme de Julie
Dans une grille 3 ´ 3, Julie a écrit
trois nombres : (a - 12), a et (a + 4) dans
les positions illustrées. Elle veut compléter la grille pour que la
somme des éléments soit la même dans chaque rangée horizontale,
verticale et diagonale.
Montrez que cette somme est plus
petite que 3a.
70. Fleurs de Clara
Tout en pensant à son jardin, Clara
veut placer chacun des nombres de 1 à 11 dans les cellules ci-après.
La somme doit être la même dans chacune des rangées de trois cellules
reliées par une droite.
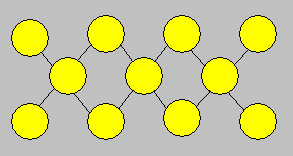
Montrez que la somme dans
chacune des rangées ne peut pas être 15.
71. Passage de la vie
Dans cette addition, chaque lettre
représente un chiffre différent.
Montrez que A ne peut pas être
égal à 5.
72. Suite de Roxanne
Roxanne a écrit les cinq premières
lignes d’une suite en un triangle comme ci-après. Le premier terme
est 2 et chaque autre terme est augmenté de 3. Elle continue la suite
selon le même modèle.
|
2
5 8
11 14 17
20 23 26 29
32 35
38 41 44 |
Montrez que la somme des nombres
de chaque ligne est supérieure au cube du rang de la ligne.
73. Triangle de
Violette
Violette a tracé un grand triangle
partagé en quatre petits triangles. Elle veut écrire chacun des
nombres de 1 à 6 dans les cases des sommets. À l’intérieur de trois
petits triangles, la somme des sommets est indiquée.
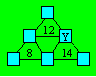
Montrez que, peu importe la
façon de répartir les nombres, le 6 est toujours dans la position Y.
74. Pairs de Pauline
Pauline fait la somme des nombres pairs
à partir de 2. Ainsi, elle a écrit :
2
+ 4 = 6
2
+ 4 + 6 = 12
2
+ 4 + 6 + 8 = 20
Montrez que la somme des nombres
consécutifs pairs à partir de 2 ne peut pas être 654 324.
75. Nonantie de
Désiré
Désiré doit choisir neuf nombres dans
ce tableau de telle sorte que leur somme soit 2000.
|
181 |
189 |
184 |
195 |
|
188 |
203 |
456 |
182 |
|
198 |
185 |
204 |
186 |
Montrez qu’il existe
exactement trois triplets de nombres dont la somme est 2000.
76. Ber d’Albert
Albert rêve à son berceau. Il veut
écrire les nombres de 1 à 8 dans les cases de ce ber. La somme doit
être la même dans chaque rangée de trois ou de quatre cases reliées
par une droite.
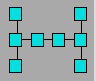
Montrez que la somme des nombres
de chaque rangée ne peut pas être 14.
77. Coupure de Major
Major a placé six rangées de boules en
un triangle comme ci-après. Il a tracé une droite entre la quatrième
et la cinquième rangée. La partie supérieure contient 10 boules et l’inférieure
11 boules.

Montrez qu’un triangle de
boules ne peut pas être partagé en deux parties égales lorsque le
nombre de rangées est de la forme 4m + 1.
78.
Oursons d’Alice
Alice fabrique neuf oursons et les
numérote de 1 à 9. Elle dit à Aimée :
- Dispose
les oursons en un triangle comme ci-après pour que la somme des
numéros soit 18 sur chaque côté du triangle.

Montrez qu’il est impossible
de disposer les oursons.
79. Années triples
Zoé presque centenaire s'inspire de
trois années du 21e siècle pour écrire cette expression :
200233 + 200533 + 200833
Montrez que cette expression est
un multiple de 3.
80. Cellules de Laure
Laure désire placer chacun des nombres
de 1 à 9 pour que la somme soit 13 dans chaque rangée de deux, de
trois ou de quatre cellules reliées par une droite.
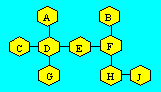
Montrez qu’une seule
disposition est possible. Le fait de pouvoir intervertir des nombres
dans une même rangée ne constitue pas une nouvelle disposition.
81. Trios généreux
Soit a, b, c et d
quatre entiers où b = a + 1 et d = c + 1.
Montrez que, pour chaque valeur
de a, il existe un trio (a, b, c) pour
lequel a2 + b2 + c2
= d2.
82. Totaux différents
Jean-Nil écrit chacun des nombres de 1
à 9 dans les deux carrés ci-après. Il trouve d’abord la somme de
chacune des rangées horizontales, verticales et diagonales ;
puis, il fait le total des huit rangées pour chaque carré. Le total
pour le premier carré est 119 et celui pour le deuxième carré est
121.
|
9 |
4 |
8 |
|
1 |
6 |
2 |
|
2 |
1 |
5 |
|
8 |
9 |
5 |
|
3 |
6 |
7 |
|
7 |
4 |
3 |
Montrez que la différence
des totaux est 2, sans faire l’addition rangée par rangée.
83. Histoire marine
Le marin Jules a écrit l’addition
ci-après. Chaque lettre représente un chiffre différent.
|
M A R I N
+ B
U T I N
B A T E
A U |
Montrez que M ne peut pas avoir
une valeur inférieure à 9.
84. Nobles billes
Royal a une bille et il reçoit chaque
jour trois fois le nombre de billes du jour précédent plus 1. Par
exemple, il reçoit 1, 4, 13, 40, 121, ... billes. Majesté a aussi une
bille et elle reçoit chaque jour trois fois le nombre de billes du jour
précédent plus 2. Par exemple, elle reçoit 1, 5, 17, 53, 161, ...
billes.
Montrez que, pour n’importe
lequel jour, Majesté recevra autant de billes que Royal pendant deux
jours consécutifs, soit ce jour-là et le précédent.
85. Pentagone de Carl
Carl dessine le pentagone ci-après. Il
écrit cinq nombres dans les triangles intérieurs. Il additionne les
nombres de chaque couple de triangles adjacents et écrit les résultats
sur les sommets du pentagone. Parmi les nombres de 1 à 10, le 4
apparaît deux fois et le 8 est absent. Maintenant, Carl veut écrire
chacun des nombres de 1 à 10 dans cette figure.
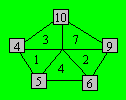
Montrez que cette tâche est
impossible à réaliser.
86.
Écureuil éveillé
En vue de l'hiver, les écureuils Roussi
et Rousso ont fait des provisions de noix. Roussi qui est moins volage a
travaillé neuf jours de plus que Rousso. Chacun a récolté le même
nombre de noix par jour que le nombre de jours affectés à la
cueillette. Ainsi, si l'un a travaillé pendant 32 jours, il a récolté
32 noix par jour. Après avoir fait le décompte des deux récoltes,
Roussi dit à Rousso :
-
Nous avons ensemble 1318 noix.
-
C'est impossible, de reprendre Rousso sur-le-champ.
Montrez que les deux écureuils
n’ont pas pu cueillir 1318 noix.
87. Pommes de Samuel
Samuel place devant lui trois paniers
contenant chacun 144 pommes. Il distribue en parts égales le contenu de
l’un entre neuf enfants, de l’autre entre 11 enfants et du
troisième entre 13 enfants. Il reste deux pommes qui ne sont pas dans
même panier.
Montrez que 144 est la plus
petite quantité qui permet un reste de deux pommes.
88. Rames de Raymond
Raymond qui a eu une mauvaise
expérience sur l’eau a écrit l’addition suivante. Chaque lettre
représente un chiffre différent.
|
R A M E
+
R I M A
L I M B E |
Montrez que I ne peut pas être
impair.
89. Carrés d’Émile
Émile écrit les égalités suivantes.
1 + 3 = 4
1 + 3 + 5 = 9
1 + 3 + 5 + 7
= 16
Montrez que la somme des nombres
impairs consécutifs à partir de 1 est un carré.
90. Un H croisé
Henriot a dessiné la figure
ci-après. Il veut placer les chiffres de 1 à 7 pour que la somme soit
13 dans chacune des cinq rangées de trois cellules reliées par une
droite.
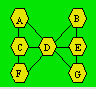
Montrez que la somme, dans
chaque rangée, ne peut pas être 13.
91. Foin de Clovis
Une araignée se promène sur un
treillis de brins de foin. Elle part du point supérieur gauche et doit
se rendre à l’autre point. Après avoir passé par un brin, elle le
fait exploser. Son maître Clovis veut qu’elle passe par 16 brins de
foin.

Montrez que cette recommandation
est impossible à réaliser.
92. Suite au cube
En pensant aux cubes, Réjeanne a écrit
la suite ci-après. Le cube de 4 est 64. Elle divise ce nombre par 9 ;
le reste est 1. Le cube de 7 est 343. Elle divise ce nombre par 9 ; le
reste est 1.
1, 4, 7, 10, 13, ...
Montrez que, si l'on élève
chaque terme de cette suite au cube et si l'on divise le résultat par
9, le reste de la division est toujours 1..
93. Cour d’école
Dans une cour d’école, il y a neuf
balançoires disposées trois par trois. On demande aux 108 élèves d’occuper
les balançoires. Le nombre d’élèves doit être le même
horizontalement, verticalement et en diagonale. Chaque balançoire
reçoit un nombre différent d’élèves. Celle la moins occupée en
reçoit cinq.

Montrez qu’aucune balançoire
ne peut recevoir plus de 19 élèves.
94. Boîtes d’Antoine
Antoine a décidé de placer les nombres
de 1 à 11 dans cette figure de telle manière que la somme est 17 dans
chaque rangée de trois boîtes reliées par une droite.
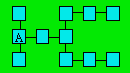
Montrez que la boîte A ne peut
accueillir que 2.
95. Dominos de Rachel
Rachel ampute les cases des quatre coins
d’une grille 5 × 5. Elle veut placer des dominos sur cette grille
tronquée.
Montrez qu’elle peut y
déposer au maximum neuf dominos.
96. Étoile de Luce
Luce a écrit les nombres de 1 à 12
dans l’hexagramme de gauche. La somme des nombres dans chaque rangée
de quatre cases est 26. Luce prend la suite des nombres impairs comme 1,
3, 5, 7, etc. Elle écrit ces entiers dans la seconde figure en
respectant l’ordre numérique de la première.
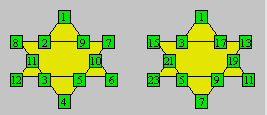
Montrez que, dans le second
hexagramme, la somme des quatre nombres de chaque rangée est la même.
97. Solitaire d’Étienne
Étienne trace une grille 4 × 4. Il y
place deux jetons bleus (B), deux jetons noirs (N) et deux jetons rouges
(R), comme il est montré dans la figure de gauche. Il déplace les
jetons un à un. Il les fait sauter horizontalement, verticalement ou
obliquement par-dessus un autre pour se poser sur une case libre et
adjacente au jeton sauté. À la fin, il doit obtenir la figure de
droite.
|
R |
N |
R |
N |
|
|
|
|
|
|
|
B |
B |
|
|
|
|
|
|
|
|
|
|
|
® |
|
R |
N |
|
|
|
|
|
|
|
B |
R |
N |
B |
Montrez qu’il est impossible d’obtenir
la figure de droite.
98. Triangle d’Alberte
Dans les cercles de ce triangle, Alberte
veut placer chacun des nombres de 1 à 6 pour que la somme soit la même
sur chaque côté du triangle..
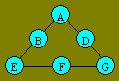
Montrez que, peu importe la
somme de chaque rangée, la somme des nombres des coins est toujours un
multiple de 3.
99. Noix d’Isaac
Isaac a acheté 7 635 noix qu’il
veut répartir en deux sacs. Chacun doit contenir un nombre carré de
noix.
Montrez qu’il est impossible
de partager les noix en deux carrés.
100. Cailloux de
Tristan
Tristan a divisé son parterre en 15
parcelles comme ci-après. Dans chaque parcelle, sauf celles du bas, le
nombre de cailloux doit être égal au total des cailloux qui se
trouvent dans les deux parcelles inférieures. Émilie a placé 3, 4, 5,
6, 7 cailloux à la base, mais pas dans cet ordre. Elle a ainsi disposé
88 cailloux au sommet. Elle voudrait avoir, à la base, au moins
une autre suite d’entiers consécutifs, tout en ayant 88 cailloux au
sommet.
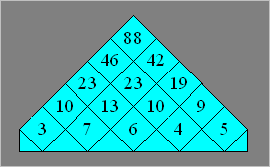
Montrez qu’il y a une seule
autre suite d’entiers consécutifs qui permet de disposer 88 cailloux
au sommet.
![]()
![]()