****************
Récréations
1 à 50
****************
Ce recueil contient 100
récréations pour lesquelles il faut faire une démonstration. Une solution
détaillée est donnée pour chaque problème. Les solutions que nous
présentons s’appuient, en grande partie, sur les propriétés des nombres
et des réseaux.
Nous proposons des problèmes
puisés dans diverses classes qui constituent les mathématiques
récréatives. Le lecteur pourra développer et appliquer des stratégies
qui lui serviront dans d’autres domaines des mathématiques.
Amusez-vous bien.
* * * * * * * * * * * * * * * *
1.
Céline roule
Céline veut disposer chacun des nombres de 1 à 9 dans les cases de la
roue ci-après. La somme doit être la même sur chaque rayon.
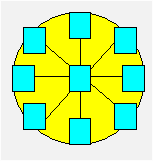
Montrez que toute somme possible est
un multiple de 3.
2. Bien de Raymond
Raymond a écrit l’addition suivante dans
laquelle chaque lettre représente un chiffre différent.
|
M O N
+
M E S
M A
B
I E N |
Montrez que M + O est égal à 9.
3. Suite d’Ariane
La jeune fille d’Ariane se met à compter
de 4 en 4. Alors, Ariane s’empresse d’écrire cette suite :
1, 5, 9, 13, 17, 21, ...
Montrez que tous les carrés impairs
se trouvent dans cette suite.
4. Doudou d’Éliane
Éliane prend un cavalier le pose sur la
case 1 de la grille 4 ´
4. Elle le déplace comme aux échecs, soit en L.
Montrez qu’un cavalier qui part d’un
coin peut parcourir au plus 15 cases.
5. Gabarit de Mathieu
Mathieu désire placer chacun des nombres de
1 à 8 dans les cercles de ce gabarit. La somme doit être la même dans
chaque rangée de deux ou de trois cercles joints par une droite.

Montrez que la seule somme possible
est 12.
6. Un nez zen
Malorie fait les deux additions suivantes
dans lesquelles chacune des trois lettres correspond à un chiffre
différent.
|
N E Z
+
Z N E |
E N Z
+
Z E N |
Elle soustrait le plus petit
résultat du plus grand. Montrez que la différence des deux sommes est un
multiple de 9.
7. Perles de Roussin
Dans un entrepôt, il y a à perte de vue
des caisses de perles sans grande valeur. Dans chaque caisse, la quantité
de perles est un nombre élevé à la puissance 4. Roussin désire acheter
deux caisses ayant en tout 8764 perles.
Montrez qu’aucun groupe de deux
caisses ne peut contenir 8764 perles.
8. Un lapin frustré
Magloire dispose 25 roches en un carré 5 ´
5. Un lapin peut se déplacer d’une roche à une autre voisine
horizontalement ou verticalement.
Montrez que le lapin peut fouler
toutes les roches mais, ce faisant, ne peut pas terminer sa course au point
de départ.
9. Triangle dense
Marcelle a préparé le triangle ci-après.
Elle veut y placer sept nombres de façon que la somme des nombres de chaque
rangée de trois cellules reliées par une droite soit la même.
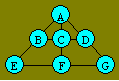
Montrez que la somme totale des
éléments est égale à 7 fois A.
10. Hommage à Gardner
Marius a trouvé dans un livre écrit par
Martin Gardner la figure ci-après. Les nombres consécutifs de 1 à 19 sont
répartis dans autant de cellules. La somme des nombres dans les rangées
verticales et obliques de trois, de quatre et de cinq cellules est 38.

Montrez que cette somme est la seule
possible.
11. Années au centuple
Zoé qui est
presque centenaire est impressionnée par le début du 21e
siècle. Elle a écrit :
2002100
+ 2003100 + 2004100
Montrez que cette somme n’est pas
divisible par 5.
12. Vers le bal
Prenez huit jetons marqués TOI, AM et BLE.
Placez-les dans la grille de gauche. Faites glisser les jetons sur une case
vide horizontalement ou verticalement. À la fin, vous devez obtenir la
configuration de droite.
|
T |
O |
I |
|
B |
A |
L |
|
A |
M |
|
|
O |
T |
E |
|
B |
L |
E |
|
M |
I |
|
Montrez qu’il est impossible de
réaliser cette tâche en 18 mouvements ou moins.
13. Horace cause
De sa causeuse, Horace veut écrire les
nombres de 1 à 8 dans les cases pour que la somme soit 15 dans chaque
rangée de trois ou de quatre cases reliées par une droite.
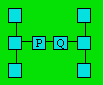
Montrez que P + Q = 6 lorsque la
somme est 15 dans chaque rangée.
14. Sommes de Vincent
Vincent a écrit l'expression suivante où
chaque lettre représente un chiffre différent de 1 à 6.
AB + CD + DE
Montrez que 10 sommes sont
possibles.
15. Cavalier de Patricia
Dans une grille 5 ´
5, Patricia a déplacé le cavalier à partir de la
case numérotée 1. Voici le chemin suivi :
|
1 |
24 |
19 |
14 |
3 |
|
18 |
13 |
2 |
9 |
20 |
|
25 |
8 |
23 |
4 |
15 |
|
12 |
17 |
6 |
21 |
10 |
|
7 |
22 |
11 |
16 |
5 |
Montrez que le cavalier peut
parcourir au moins 24 cases lorsque son point de départ est n’importe
quelle case blanche.
16. Médian de Vincent
Vincent a composé le carré magique d’ordre
3 ci-après. La somme des nombres (ou densité) dans chaque rangée
horizontale, verticale et diagonale est 78. Le nombre du milieu 26 est le
tiers de la densité.
|
37 |
12 |
29 |
|
18 |
26 |
34 |
|
23 |
40 |
15 |
Montrez que, dans tout carré
magique d’ordre 3, le nombre du milieu est toujours égal au tiers de la
densité.
17. Désaccord de filles
Anabelle trace six cercles comme ci-dessous.
Elle désire placer chacun des nombres de 1 à 6 dans les cercles pour que l’addition
soit vraie.
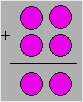
Montrez qu’il est impossible de
placer les nombres de 1 à 6 dans ce diagramme.
18. Carmen divisée
Arthur a écrit un nombre de six chiffres
différents et l’a représenté par CARMEN.
Montrez que si CARMEN est divisible
par 13, CAR - MEN est aussi divisible par 13.
19. Fleurs d’Émilie
Émilie a divisé son parterre en 15
parcelles carrées comme ci-après. Dans chaque parcelle, le nombre de
fleurs doit être égal au total des fleurs qui se trouvent dans les deux
parcelles inférieures. Émilie a planté 2, 3, 4, 5, 6 fleurs à la base,
mais pas dans cet ordre. Elle a ainsi planté 65 fleurs au sommet. Elle
voudrait avoir, à la base, au moins une autre suite de nombres
consécutifs, mais pas nécessairement dans cet ordre, tout en ayant 65
fleurs au sommet.
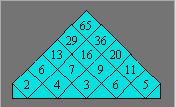
Montrez qu’il n’y a pas d’autres
suites d’entiers consécutifs qui permettent de planter 65 fleurs au
sommet.
20. Suite de Fleuron
Fleuron a écrit les premiers termes de la
suite ci-après : La différence est 3 entre chaque terme.
2, 5, 8, 11, 14, 17, ...
Montrez qu’il n’y a pas de
carré dans cette suite.
21. Initiale de Mathias
Dans la figure ci-après, Mathias désire
placer chacun des nombres de 1 à 9 pour que la somme soit 17 dans chaque
rangée de trois cellules reliées par une droite.
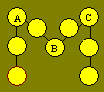
Montrez que les cellules A et C
doivent recevoir respectivement les nombres 8 et 9.
22.
Racine de Pascale
Pascale fait la somme des trois résultats
suivants :
1.
un entier élevé au carré.
2.
l'entier qui le suit élevé au carré.
3.
le carré du produit des deux premiers résultats.
Puis, elle extrait la racine carrée
de la somme. Par exemple, si elle choisit 12 comme entier, le résultat
final est 157.
|
122 = 144
132 = 169
(12 × 13)2 = 24 336
Somme : 24 649
Ö24
649 = 157 |
Montrez que le même résultat peut
être obtenu en faisant la somme des deux carrés, en divisant par 2 cette
somme et en arrondissant le quotient à l’entier supérieur.
23. Neveu de Philippe
Philippe demande à son neveu de placer
chacun des nombres de 2 à 10 dans les cases de façon à réaliser trois
additions.
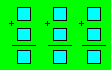
Montrez qu’il y a un seul ensemble
de trois sommes qui est possible.
24. Lapin d’Angélie
Trente-six cailloux sont disposés en un
carré 6 × 6. Angélie a placé une carotte sur chaque caillou. Un lapin
part d’un caillou ; il se déplace horizontalement et verticalement.
Il mange chaque carotte qu’il atteint.
Montrez qu’un lapin peut manger
toutes les carottes, peu importe son point de départ.
25. Rectangle d’Adamis
Adamis veut placer les nombres de 1 à 10
pour que la somme soit 17 dans chacune des quatre rangées de trois ou de
quatre cases en périphérie.
Montrez que la somme ne peut pas
être 17.
26. Somme de Maya
En utilisant chacun des chiffres de 1 à 9,
Maya a écrit l’addition ci-après. Chaque lettre représente un
chiffre différent.
AB + CD + EF + GH + J = 189
Montrez qu’il est impossible que
la somme soit 204.
27. Coins de Fabrix
Fabrix a composé le carré magique d’ordre
3 ci-après. La densité ou somme des nombres dans chaque rangée
horizontale, verticale et diagonale est 54. La somme des nombres des quatre
coins est 72, ce qui est quatre fois le nombre du milieu (ou médian).
|
26 |
7 |
21 |
|
13 |
18 |
23 |
|
15 |
29 |
10 |
Montrez que, dans tout carré
magique d’ordre 3, la somme des nombres des quatre coins est égale à
quatre fois le médian.
28. Cavalier de Line
Dans une grille 5 × 5, Line a déplacé le
cavalier à partir de la case numérotée 1. Voici le chemin suivi :
|
1 |
24 |
19 |
14 |
3 |
|
18 |
13 |
2 |
9 |
20 |
|
25 |
8 |
23 |
4 |
15 |
|
12 |
17 |
6 |
21 |
10 |
|
7 |
22 |
11 |
16 |
5 |
Montrez que le cavalier peut
parcourir toutes les cases de cette grille lorsque son point de départ est
une case grise.
29. Oiseaux de Philippe
Dans l’article
Quand
les oiseaux volent, nous avons introduit un symbole qui exprime
la puissance triangulaire d'un entier naturel donné. On peut donc écrire :
|
1D =
1 2D
= 3 3D
= 6 4D
= 10 5D
= 15
6D = 21
7D = 28
8D = 36 9D
= 45 |
À l’inverse, on peut extraire la
racine triangulaire d’un nombre. Ainsi, 9 est la racine triangulaire de
45. Philippe a trouvé un algorithme pour extraire la racine d’un
triangulaire.
1.
On multiplie le nombre donné par 8 et on additionne 1 au produit.
2.
On extrait la racine carrée.
3.
On soustrait 1 et on divise par 2.
Le
résultat est la racine triangulaire.
Montrez que cet algorithme est
valide.
30. Victor partage
Victor choisit un nombre. Il le partage en
quatre parties a, b, c, d. Il additionne 6 à a,
soustrait 5 à b, multiplie c par 4 et divise d
par 3.
Montrez que la somme des quatre
parties est 2a + 13c + 11, lorsque le résultat de chacune des
quatre opérations est identique.
31. Frère de Jocelyn
Jocelyn demande à son petit frère de placer
chacun des nombres de 1 à 9 dans les cases de façon à réaliser trois
soustractions.
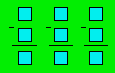
Montrez qu’il est impossible de placer
ces nombres.
32. Claudine multiplie
Claudine veut faire la multiplication ci-après
dans laquelle chacune des lettres représente un chiffre différent. Les deux
nombres doivent contenir les 10 chiffres de 0 à 9.
57AB02 × CDE8 = ?
Montrez que le produit est un multiple
de 36 si A + B = 7.
33.
Macarons d’Alexis
Alexis prend 11 macarons et les numérote de 1
à 11. Il dit à Alexia :
- Tu dois placer
un macaron par cellule. La somme des numéros doit être la même dans chaque
rangée oblique de trois macarons.

Montrez que la plus petite somme
possible par rangée oblique est 16.
34. Multiples de Léonie
Léonie écrit les nombres de 1 à 50. Elle met
entre parenthèses des groupes de trois nombres consécutifs et les additionne.
Par exemple, elle fait : 28 + 29 + 30 = 87. Le nombre 87 est un multiple de
3. Elle prend d’autres trios. La somme est toujours un multiple de 3.
Montrez que la somme de trois nombres
consécutifs est toujours un multiple de 3.
35. Marque de Florence
Florence a écrit son nom sous forme d’une
addition. Chaque lettre représente un chiffre différent.
Montrez qu’aucune somme possible n’est
inférieure à 381.
36. Huard de Laura
La pièce d’un dollar du Canada montre un
huard. Laura prend une pièce et l’entoure de six autres pièces. Toutes les
pièces touchent à la pièce centrale et se touchent entre voisines.
Montrez que six pièces sont
nécessaires et suffisantes pour former la couronne d’une première pièce.
37. Carrés de Raoul
Raoul a composé le carré magique d’ordre 3
ci-après. La somme est 54 dans chaque ligne, colonne et diagonale. Il
écrit : 232 + 102 + 212 = 152
+ 262 + 132 = 1070.
|
23 |
10 |
21 |
|
16 |
18 |
20 |
|
15 |
26 |
13 |
Montrez que, dans tout carré magique d’ordre
3, la somme des carrés des éléments de la première ligne est égale à la
somme des carrés des éléments de la troisième ligne.
38. Damier de Josias
Josias a construit un damier 10 ´
10 pour son oncle. Il demande un euro pour la première case, quatre euros pour
la deuxième, sept euros pour la troisième, ainsi de suite en augmentant de
trois euros par case.
Montrez que le double du montant
demandé pour la 99e case, diminué du montant de la 100e
case, est égal au montant de la 98e case.
39. Choix de Bernard
Bernard choisit un nombre de cinq chiffres. Il
fait la somme des chiffres de ce nombre et soustrait cette somme du nombre
choisi. Par exemple, s’il a choisi 36 548, il fait : 3 + 6 + 5 + 4 + 8 =
26 et 36 548 - 26 = 36 522. Le résultat est un multiple de 9.
Montrez que le résultat est toujours un
multiple de 9.
40. Cinq de Malorie
Malorie a écrit l’addition suivante. Chaque
lettre correspond à un chiffre différent.
|
C I N Q
+ C I N Q
D
I X O |
Montrez que la plus grande valeur de
CINQ est 4036.
41. Initiale de Xavier
Xavier dessine le treillis ci-après. Il désire
y inscrire chacun des nombres de 1 à 8 de telle manière que la somme dans
chacune des cinq rangées de trois cercles reliés par une droite est 12.
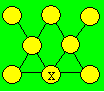
Montrez qu’il est impossible d’inscrire
5 dans la cellule où Xavier a écrit son initiale.
42. Poules géantes
Au pays des Œufs géants, le grand chef
possède un poulailler de 1321 poules. Il demande à son adjoint de
regrouper les poules en trois enclos. L’enclos du milieu doit avoir 45
poules de plus que l’enclos de gauche et 54 poules de moins que l’enclos
de droite.
Montrez qu’il est impossible de faire
ces groupes.
43. Billes de Rosario
Rosario partage ses billes en groupes de 3, 7,
11 et 15. Son père qui l'observe écrit cette suite :
3, 7, 11, 15, 19, ...
Montrez que le reste est 1 lorsqu’on
divise par 4 le carré de chaque terme de cette suite.
44. Magie de Margot
Margot a écrit 7, 3 et 9 sur la première ligne
d’un carré 3 × 3. Elle désire compléter le carré pour que la somme de
chacune des rangées horizontales, verticales et diagonales (ou densité) soit
la même.
Montrez qu’il est impossible de
construire un carré magique avec des entiers, lorsqu’une rangée contient 7,
3 et 9.
45. Soldats de plomb
Le prof Idéal a donné le problème suivant à
ses élèves : "Alphonse et Bérénice ont ensemble 37 soldats de
plomb. Bérénice et Caroline ont ensemble 27 soldats de plomb. Caroline et
Alphonse ont ensemble 17 soldats de plomb."
Montrez que ce problème n’est pas
réaliste.
46. Trios de Raynold
Raynold écrit les nombres de 1 à 20. Il met
entre parenthèses des groupes de trois nombres consécutifs et les multiplie.
Par exemple, il fait :13 × 14 × 15 = 2730. Le nombre 2730 est divisible
par 6. Il fait d’autres essais. Le produit est toujours divisible par 6.
Montrez que le produit de trois nombres
consécutifs est toujours divisible par 6.
47. Mission de Malo
Malo a tracé une grille rectangulaire 3 × 4.
Il désire placer les nombres de 1 à 12 pour que la somme soit identique dans
chaque rangée horizontale et identique, mais différente de la première, dans
chaque rangée verticale.
Montrez que cette tâche est impossible
à réaliser.
48. Voisins d’Alex
Alex écrit la suite ci-après. Il note que les
différences successives entre deux termes voisins sont 2, 3, 4, 5, 6, 7, etc.
1, 3, 6, 10, 15, 21, 28, ...
Montrez que si on multiplie par 8 chaque
terme de la suite et qu’on additionne 1 au produit, le résultat est un
carré.
49. Suite de Paélie
Paélie a composé un carré magique d’ordre 3
avec chacun des entiers de 1 à 9. La somme dans chaque rangée horizontale,
verticale et diagonale est 15.
Montrez qu’on peut construire un
carré magique d’ordre 3 avec toute suite de neuf entiers consécutifs.
50. Initiale d’Arsène
Arsène veut écrire les nombres de 1 à 9 dans
les cellules de cette figure. Il désire que la somme soit 19 dans chaque
rangée de quatre cellules reliées par une droite.
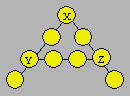
Montrez que X + Y + Z = 12.
![]()
![]()