**************
Solutions 1 à 50
**************

Solution 1. La somme des nombres de 1 à 9 est 45. On compte quatre rayons. La case du centre apparaît dans quatre rangées. Soit C l’élément du centre qui peut varier de 1 à 9, A la somme des éléments des autres cases. En regard de chaque élément, on fait : (A + 4C)/4, comme l’indique le tableau.

La dernière ligne donne les sommes. Or, seuls 12, 15 et 18 sont possibles. 

D’où, toute somme possible est un multiple de 3.

Solution 2. A + S = 10, car N + S + A = N (colonne des unités) : ce qui amène une retenue de 1 au-dessus de la colonne des dizaines. Alors, 1 + O + E + M = E (colonne des dizaines) et 1 + O + M = 0. 

En conséquence, M + O = 9.

Solution 3. Soit 2n + 1 un nombre impair, son carré est 4n² + 4n + 1. Quand on divise le carré par 4, le reste est 1. D’où, ces carrés sont de la forme 4m + 1. Or, le terme général de la suite donnée est 4m + 1. 

D’où, tous les carrés impairs sont dans cette suite.

Solution 4. Lorsque le cavalier quitte la case 1, il atteint une des quatre cases du centre. Pour atteindre une autre case d’un coin, il doit partir d’une des trois cases libres du centre et revenir dans une de ces deux cases. Il reste alors une seule case libre au centre. Pour atteindre la troisième case du coin, le cavalier devra partir de la seule case libre du centre. Il restera alors prisonnier dans le coin. Une case d’un coin ne sera pas visitée. Voici un exemple de parcours d’un cavalier :

Donc, un cavalier qui part d’un coin d’une grille 4 × 4 peut parcourir au plus 15 cases.

Solution 5. On ajoute un cercle dans le coin supérieur droit. On y place 0. La somme des nombres de 0 à 8 est 36. Il y a trois rangées horizontales (ou verticales). On fait : 36 ÷ 3 = 12. 

En conséquence, la seule somme possible est 12. Voici un exemple :

Solution 6. En soustrayant les deux sommes, on peut écrire : (NEZ - ZEN) + (ZNE - ENZ). Ce sont deux couples de nombres renversés. La différence de deux nombres renversés est un multiple de 9. En effet, soit le nombre 100a + 10b + c, son renversé est 100c + 10b + a. La différence des deux est 99a - 99c, un multiple de 9. Aussi, (NEZ - ZEN) est un multiple de 9, de même que (ZNE - ENZ). Quand on additionne deux multiples de 9, on obtient un troisième multiple de 9. 

La différence des deux sommes est un multiple de 9.

Solution 7. Le dernier chiffre d’un nombre élevé à la puissance 4 est 0, 1, 5, 6. Comme on a deux caisses, on fait la somme des unités comme suit :

Or, 8764 se termine par 4 et 4 n’apparaît pas dans le tableau. 

Aucun groupe de deux caisses ne contient 8764 perles.

Solution 8. Le lapin peut fouler toutes les roches. En voici un exemple :

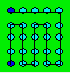
Soit (L, C) où L est la ligne et C la colonne, le lapin se déplace de (1,1) à (1, 2) ou à (2, 1), de (1, 2) à (1, 1), à (1, 3) ou à (2, 2), etc. D’une roche à l’autre, la somme des coordonnées passe de paire à impaire ou de impaire à paire. Selon cette règle d’alternance, si au départ la somme est paire, elle devra être aussi paire à la 25^e roche. Si, au départ, la somme est impaire, elle devra être aussi impaire à la 25^e roche. Le passage de la 25^e roche à la première ne peut pas se faire, car elles ont la même parité. 

En conséquence, le lapin ne peut pas terminer sa course au point de départ.

Solution 9. Soit S la somme totale et s la somme des éléments de chaque rangée,

A + E = C + D, car A + B + E = B + C + D

A + F = B + D, car A + C + F = B + C + D

A + G = B + C, car A + D + G = B + C + D

En additionnant, membre à membre, ces trois égalités, on obtient :

3A + E + F + G = 2B + 2C + 2D

3A + s = 2s

D’où, 3A = s

Or, S = A + B + C + D + E + F + G

S = A + s + s

S = A + 3A + 3A

D’où, S = 7A.

Donc, la somme totale des éléments est égale à 7 fois A.

Solution 10. Soit S la somme par rangée. On compte 15 rangées. On obtient 15S. Chaque cellule est à l’intersection de trois rangées. On divise 15S par 3. On obtient 5S. La somme des entiers de 1 à 19 est 190. On fait : 5S = 190. D’où, S = 38. 

Il ne peut pas y avoir d’autres sommes possibles que 38.

Solution 11. Le tableau indique le dernier chiffre pour chaque puissance de 1 à 5.

Comme la puissance 5 a les même chiffres que la puissance 1, un nouveau cycle débute à cette puissance. De là, la puissance 100 a les mêmes chiffres que la 4. On additionne ces trois chiffres : 6 + 1 + 6 = 13. Le dernier chiffre est 3. Aucun nombre se terminant par 3 n’est divisible par 5. 

L’expression n’est pas divisible par 5.

Solution 12. Pour chaque lettre, on vérifie le nombre de mouvements nécessaires pour atteindre la configuration finale. T (2), O (2), I (3), A (2), M (2), case vide (1), B (2), L (3), E (1) : ce qui fait 18 mouvements. 

Comme il faut déplacer d’autres jetons, il est impossible de réaliser cette tâche en moins de18 mouvements.

Note : Voici une façon de réaliser cette tâche en 35 mouvements : M, L, E, M, I, O, T, A, B, E, M, I, O, T, L, O, T, L, A, B, O, T, I, M, E, O, T, E, M, I, E, T, O, M, I.

Solution 13. On fait : 3 × 15 = 45, car il y a trois rangées. La somme des nombres de 1 à 8 est 36. On fait : 45 - 36 = 9. La somme des cases extrêmes de la rangée horizontale est 9, car ces cases appartiennent à deux rangées. Comme la somme de chaque rangée est 15, on fait : 15 - 9 = 6. Donc, P + Q = 6. Une configuration est :

Solution 14. Pour avoir la plus petite somme, on donne les valeurs 1, 2, 3 aux dizaines et 4, 5, 6 aux unités. La somme est 75. Pour avoir la plus grande somme, on donne les valeurs 4, 5, 6 aux dizaines et 1, 2, 3 aux unités. La somme est 156. En intervertissant deux chiffres consécutifs de l’unité à la dizaine, on augmente la somme de 9. On a une suite arithmétique dont le premier terme est 75, le dernier 156 et la raison 9. 

Il y a 10 sommes possibles.

Solution 15. On se base sur le tableau donné dans le problème. Le cavalier part de la case 24. Il prend le chemin inverse et s’arrête à la case 1. La case 25 n’a pas été touchée. Le cavalier a parcouru 24 cases. À cause de la symétrie de la figure, il en est de même lorsque le cavalier part des cases blanches périphériques, soit 14, 20, 10, 16, 22, 12 et 18. Le cavalier part de la case 2 et suit le même chemin jusqu’à la case 25. Il a parcouru 24 cases. À cause de la symétrie de la figure, il en est de même lorsque le cavalier part des trois autres cases blanches centrales, soit 4, 6 et 8. 

Bref, dans tous les cas, le cavalier peut parcourir 24 cases à partir d’une case blanche.

Solution 16. On compose un carré dans lequel la densité est D.

On écrit :

a₁₁ + a₂₂ + a₃₃ = D

a₁₂ + a₂₂ + a₃₂ = D

a₁₃ + a₂₂ + a₃₁ = D

On additionne, membre à membre, ces trois égalités.

(a₁₁ + a₁₂ + a₁₃) + 3a₂₂ + (a₃₁ + a₃₂ + a₃₃) = 3D

D + 3a₂₂ + D = 3D

3a₂₂ = D

D’où, a₂₂ est égal à D/3. Le nombre du milieu est toujours égal au tiers de la densité.

Solution 17. On examine d’abord le cas où il y a une retenue au-dessus des dizaines. Pour avoir une retenue, il faut que les unités des deux nombres à additionner soient 5 et 6. L’unité de la somme est alors 1. Il reste 2, 3 et 4 pour la colonne des dizaines : ce qui est impossible. Dans le cas où il n’y a pas de retenue, les quatre chiffres des nombres à additionner doivent avoir la même somme que la somme des chiffres du résultat. Or, la somme des nombres de 1 à 6 est 21. On fait 21 ÷ 2 = 10,5. Le résultat n’est pas un entier. 

Il est impossible de placer les nombres de 1 à 6 dans ce diagramme.

Solution 18. On montre d’abord que CAR CAR est divisible par 13. On peut décomposer ce nombre ainsi : 100 000C + 10 000A + 1000R + 100C + 10A + R, ce qui est égal à 100 100C + 10 010A + 1001R. Cette somme est divisible par 1001 car chaque terme est divisible par 1001. Or, 1001 est divisible par 13. D’où, CAR CAR est divisible par 13. On fait : CAR CAR - CAR MEN = CAR - MEN. 

Comme CAR CAR et CAR MEN sont tous deux divisibles par 13, CAR - MEN est divisible par 13.

Solution 19. Soit a, a + 1, a + 2, a + 3 et a + 4 le nombre de fleurs à la base et s le nombre de fleurs au sommet. Pour avoir la plus petite valeur au sommet, on place la plus petite valeur parmi les cinq au centre de la base, puis les plus grandes aux extrémités. La plus petite valeur de s est 16a + 19. Pour avoir la plus grande valeur au sommet, on place la plus grande valeur au centre de la base, puis les plus petites aux extrémités. La plus grande valeur de s est 16a + 45. Si a = 1, la plus petite valeur est 35 et la plus grande 61. Or, 65 n’est pas dans cet intervalle. Si a = 3, la plus petite valeur est 67 et la plus grande 93. Or, 65 n’est pas dans cet intervalle. 

D’où, il n’y a pas d’autres suites d’entiers consécutifs qui permettent de planter 65 fleurs au sommet.

Solution 20. On partage les nombres en trois classes : 3n - 1, 3n, 3n + 1. Le carré de 3n - 1 est 9n² - 6n + 1. Le reste de la division de ce polynôme par 3 est 1. Le carré de 3n est 9n². Le reste de la division par 3 est 0. Le carré de 3n + 1 est 9n² + 6n + 1. Le reste de la division par 3 est 1. Or, les termes de la suite sont de la forme 3n + 2. Le reste de la division par 3 est 2. 

Il n’y a pas de carré dans cette suite.

Solution 21. La somme des nombres de 1 à 9 est 45. Les cellules marquées A, B et C sont les seules qui appartiennent à deux rangées. Comme il y a quatre rangées, on fait : 4 × 17 = 68 et 68 - 45 = 23. La somme des nombres des cellules A, B et C est 23. Les trois nombres possibles sont 6, 8 et 9. Le 8 et le 9 ne peuvent pas être dans une même rangée. Ils doivent être placés en A et en C. Donc, les cellules A et C doivent recevoir respectivement les nombres 8 et 9. Une configuration possible est :

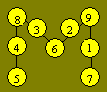
Solution 22. 1^er On généralise la première démarche. Soit n le plus petit entier, le total est n² + (n + 1)² + n²(n + 1)² = n⁴ + 2n³ + 3n² + 2n + 1. L'expression est égale à (n² + n + 1)². La racine carrée de cette dernière expression est n² + n + 1.

2^e On généralise la seconde démarche. Soit n le plus petit entier, le carré de n est n², celui de (n + 1) est n² + 2n + 1. La somme est 2n² + 2n + 1. En divisant l’expression par 2, on obtient n² + n + ½. En arrondissant ½ à l’entier supérieur, on a n² + n + 1. 

Le même résultat peut donc être obtenu en appliquant les deux démarches.

Solution 23. La somme des nombres de 2 à 10 est 54. Comme chaque somme est la moitié de la somme de trois nombres qu’on additionne, on fait : 54 ¸ 2 = 27. La somme des trois sommes est 27. L’une des sommes est 10, car ce nombre est le plus grand. Une deuxième somme est 9, car il n’y a pas de 1 pour faire : 9 + 1 = 10. La troisième somme est : 27 - 10 - 9 = 8. 

L’ensemble (8, 9, 10) est le seul possible. À titre d’exemple, on peut écrire : 3 + 7 = 10, 4 + 5 = 9 et 2 + 6 = 8.

Solution 24. Dans cet exemple, le lapin part du coin supérieur gauche et passe par tous les cailloux.

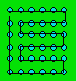
Comme il peut atteindre le caillou de départ, peu importe le point de départ, le lapin peut toucher à tous les cailloux et manger toutes les carottes.

Solution 25. Par rapport aux rangées, le total est : 17 × 4 = 68. La somme des nombres de 1 à 10 est 55. On fait : 68 - 55 = 13. La somme des nombres des quatre coins est 13. Les combinaisons possibles sont (1, 2, 3, 7), (1, 2, 4, 6) et (1, 3, 4, 5). Pour (1, 2, 3, 7), on place 1 dans un coin. Seul le 7 peut être dans un coin de la même colonne. L’autre colonne accueille 2 et 3 qui exigent 12 pour une somme de 17 : hypothèse à rejeter. Pour (1, 2, 4, 6), on place 1 dans un coin. Seul le 6 peut être dans un coin de la même colonne. L’autre colonne accueille 2 et 4 qui exigent 11 pour une somme de 17 : hypothèse à rejeter. Pour (1, 3, 4, 5), on place 1 dans un coin. Aucun autre nombre ne peut compléter la colonne : hypothèse à rejeter. 

Il est impossible que la somme par rangée soit 17.

Solution 26. La somme des chiffres de 1 à 9 est 45. La somme des chiffres de 45 est 9. La somme des chiffres du total doit être un multiple de 9. Or, la somme des chiffres de 204 est 6. 

Il est donc impossible que la somme soit 204.

Solution 27. On compose un carré magique dans lequel d est la densité et m le médian.

On écrit : a₁₁ + m + a₃₃ = d
a₁₃ + m + a₃₁ = d

On fait la somme des deux égalités.
a₁₁ + a₃₃ + a₁₃ + a₃₁ + 2m = 2d
a₁₁ + a₃₃ + a₁₃ + a₃₁ = 2d - 2m

Dans tout carré magique d’ordre 3, le médian est égal au tiers de la densité. On déduit que d = 3m. On peut écrire : a₁₁ + a₃₃ + a₁₃ + a₃₁ = 6m - 2m = 4m. 

Donc, dans tout carré magique d’ordre 3, la somme des nombres des quatre coins est égale à quatre fois le médian.

Solution 28. On se base sur la grille donnée.
1^er À cause de la symétrie, le cavalier parcourt aussi 25 cases lorsqu’il part des cases 3, 5 et 7.

2^e Le cavalier peut partir de la case 25 et reculer jusqu’à 1. À cause de la symétrie, le cavalier parcourt aussi 25 cases lorsqu’il part des cases 19, 15 et 11.

3^e Le cavalier peut partir de 13 en suivant le chemin jusqu’à 22, puis toucher 25, 24, 23, de là atteindre 12 et reculer jusqu’à 1. À cause de la symétrie, le cavalier parcourt aussi 25 cases lorsqu’il part des cases 9, 21 et 17.

4^e Le cavalier peut partir de la case du centre. Il avance sur les cases 24, 25 et 22 et suit le chemin 21, 20, 19, ... jusqu'à 1. À partir du centre, le cavalier peut reculer jusqu’à 1.

En conséquence, lorsque le point de départ est une case grise, le cavalier peut parcourir les 25 cases d’une grille 5 × 5.

Solution 29. Soit n la racine ou le rang d’un nombre triangulaire, le terme général est n(n + 1)/2. En multipliant l’expression par 8 et en additionnant 1 au produit, on obtient 4n² + 4n + 1. Sa racine carrée est 2n + 1. En soustrayant 1 et en divisant par 2, on obtient n. 

Comme, à partir du terme général, on obtient n, l’algorithme est valide.

Solution 30. On pose : a + 6 = b - 5. D’où, b = a + 11. On pose : 4c = d/3. D’où, d = 12c. On fait : a + b + c + d = a + a + 11 + c + 12c = 2a + 11 + 13c. 

La somme des quatre parties est donc 2a + 13c + 11.

Solution 31. On considère des additions au lieu des soustractions, car a - b = c est équivalent à a = b + c. La somme des nombres de 1 à 9 est 45. Or, chaque somme est égale aux deux termes à additionner. On fait : 45 ¸ 2 = 22,5. La somme des trois sommes doit être un entier. 

Donc, il est impossible de placer ces nombres

Solution 32. La somme des chiffres de 0 à 9 est 45. Puisque A + B = 7, la somme des chiffres du premier nombre est 21 et 2 + 1 = 3. La somme des chiffres du deuxième nombre est : 45 - 21 = 24 et 2 + 4 = 6. On fait : 6 × 3 = 18. D’où, le produit est un multiple de 9. Les chiffres non utilisés sont 1, 3, 4, 6 et 9. Si E = 1, on fait : 02 × 18 = 36. Si E = 3, on fait : 02 × 38 = 76. Si E = 4, on fait : 02 × 48 = 96. Si E = 6, on fait : 02 × 68 = 136. Si E = 9, on fait : 02 × 98 = 196. Tous les produits sont des multiples de 4, car le nombre formé par les deux derniers chiffres est divisible par 4. D’où, le produit des deux nombres donnés est un multiple de 4. 

Comme le produit est un multiple de 9 et de 4, il est un multiple de 36.

Solution 33. La somme des nombres de 1 à 11 est 66. Tous les éléments peuvent être comptés deux fois, sauf ceux des quatre coins qui le seront une seule fois. Pour avoir la plus petite somme, on place 8, 9, 10, 11 dans les coins. On additionne à 66 les nombres de 1 à 7 ; la somme est 94. Comme il y a six rangées, on fait : 94 ÷ 6 = 15 2/3. La plus petite somme peut être 16. On vérifie s’il existe au moins une configuration avec cette somme. En voici une :

D’où, la plus petite somme possible par rangée est 16.

Solution 34. Soit a, a + 1, a + 2 les trois nombres consécutifs, la somme est : 3a + 3 = 3(a + 1). L’expression est un multiple de 3. 

En conséquence, la somme de trois nombres consécutifs est toujours un multiple de 3.

Solution 35. Pour que la somme soit la plus petite possible, la colonne des centaines doit contenir 1 et 2, celle des dizaines 0, 3 et 4 et celle des unités 0, 5 et 6. La somme est alors 381. C’est la plus petite possible. On ne sait pas s’il y a une solution dans ce cas, mais ce n’est pas nécessaire puisque 381 est exclu. 

Donc, aucune somme n’est inférieure à 381.

Solution 36. On dessine trois pièces comme ci-après. On marque le centre de chaque pièce et on joint les centres deux à deux. On forme ainsi un triangle.

Si a est la mesure du rayon d’une pièce, chaque côté du triangle mesure 2a. Le triangle est équilatéral et ses angles mesurent 60°. Comme la mesure de la circonférence d’un cercle est de 360°, on fait : 360 ÷ 60 = 6. 

Six pièces sont donc nécessaires et suffisantes pour former la couronne d’une première pièce.

Solution 37. On construit un carré magique général. On place la variable k au centre. Dans une diagonale, on additionne et on soustrait a ; dans l’autre, on fait les deux mêmes opérations avec b. On complète les cases périphériques médianes de façon à ce que la somme soit 3k dans chaque rangée. Le carré est magique.

On élève au carré les éléments de la première et de la troisième ligne.

 (k + a)² + (k - a - b)² + (k + b)² = 3k² + 2a² + 2ab + 2b²

et (k - b)² + (k + a + b)² + (k - a)² = 3k² + 2a² + 2ab + 2b²

Dans tout carré magique d’ordre 3, la somme des carrés des éléments de la première ligne est égale à la somme des carrés des éléments de la troisième ligne.

Solution 38. On pose que la 98^e case vaut n euros, la 99^e vaudra (n + 3) euros et la 100^e (n + 6) euros. On fait : 2 × (n + 3) - (n + 6) = n. Or, n est le montant demandé pour la 98^e case. 

La proposition est donc vraie.

Solution 39. Soit N le nombre choisi et R le résultat. On écrit : N = 10 000a₁ + 1000a₂ + 100a₃ +10a₄ + a₅, puis S = a₁ + a₂ + a₃ + a₄ + a₅. Alors, N - S = 9999a₁ + 999a₂ + 99a₃ +9a₄. Chacun des termes est multiple de 9. 

Donc, le résultat est toujours un multiple de 9.

Solution 40. On pose C = 4, car C + C = D. Si I = 9, il y a une retenue et D = 9, à rejeter. Alors I = 0 et D = 8. Comme il n’y a pas de retenue au-dessus des I, N égale à, au plus, 4. Comme il y a déjà un 4, on fait : N = 3. On essaie : 39 + 39 = 78, à rejeter à cause du 8 ; 37 + 37 = 74, à rejeter à cause du 4 ; 36 + 36 = 72. D’où, NQ = 36. 

La plus grande valeur de CINQ est 4036.

Solution 41. Avec les nombres de 1 à 8, les combinaisons de trois nombres dont la somme est 12 sont (1, 3, 8), (1, 4, 7), (1, 5, 6), (2, 3, 7), (2, 4, 6), (3, 4, 5). La cellule X est placée à l’intersection de trois rangées. Or, 5 n’apparaît que deux fois dans les combinaisons. 

Il est donc impossible d’inscrire 5 dans la cellule X.

Solution 42. Soit x le nombre de poules de l’enclos du milieu, l’enclos de gauche contient (x - 4⁵) poules et celui de droite (x + 5⁴) poules. On fait : x - 4⁵ + x + x + 5⁴ = 13²¹. Cela donne : 3x = 13²¹ - 369. Comme 3x et 369 sont divisibles par 3, pour trouver une valeur à x, il faudrait que 13²¹ soit divisible par 3 : ce qui n’est pas le cas, car 13 est un nombre premier. 

En conséquence, la tâche est impossible à réaliser.

Solution 43. Le terme général est (4n - 1). Or, (4n - 1)² = 16n² - 8n + 1. Chaque terme est divisible par 4 sauf 1. Quand on divise 1 par 4, le reste est 1. 

En conséquence, le reste est 1 lorsqu’on divise par 4 le carré de chaque terme de cette suite.

Solution 44. Dans tout carré magique d’ordre 3, le nombre du milieu est égal au tiers de la densité. Or, la somme des éléments de la première ligne étant 19, la densité est 19. Ce nombre n’est pas un multiple de 3. 

En conséquence, il est impossible de construire un carré magique lorsqu’une rangée contient 7, 3 et 9.

Solution 45. On fait : A + B = 37, B + C = 27 et C + A = 17. On fait la somme de ces trois équations. On obtient : 2A + 2B + 2C = 81. En divisant chaque membre par 2, on obtient : A + B + C = 40½. Il n’existe pas de fraction de soldat de plomb. 

Donc le problème n’est pas réaliste.

Solution 46. Dans chaque groupe de trois nombres, il y a au moins un nombre pair, soit un nombre divisible par 2. Il y au moins un nombre divisible par 3. On fait 2 × 3 = 6. 

Le produit de trois nombres consécutifs est toujours divisible par 6.

Solution 47. La somme des nombres de 1 à 12 est 78. Comme la somme est identique dans chaque rangée horizontale, elle doit être : 78 ÷ 3 = 26. Comme la somme est identique dans chaque rangée verticale, elle doit être : 78 ÷ 4 = 19,5. Cela est impossible, car on a seulement des entiers. 

En conséquence, la tâche est impossible à réaliser.

Solution 48. Soit m le terme général de la suite et n le rang des termes. On établit le tableau suivant.

Le terme général m est : n(n + 1)/2. On fait : [n(n + 1)/2 ´ 8] + 1. Cela donne : 4n² + 4n + 1 = (2n + 1)². Le résultat est le carré de (2n + 1). 

Donc, le résultat est un carré.

Solution 49. Soit s la somme des nombres de chaque rangée d’un carré magique d’ordre 3, si on additionne un même nombre c à chaque élément, la somme des nombres de chaque rangée du nouveau carré est s + 3c. Comme cette somme est unique, le nouveau carré est magique. Pour avoir toutes les suites d’entiers consécutifs, on additionne c à chaque élément de la suite initiale. 

En conséquence, toute suite de neuf entiers consécutifs forme un carré magique.

Solution 50. Trois cellules (X, Y et Z) appartiennent à deux rangées et les six autres à une seule rangée. La somme des nombres de 1 à 9 est 45. Comme la somme dans chaque rangée est 19, on fait : 19 × 3 = 57 et 57 - 45 = 12. La différence est la somme des nombres des trois cellules qui appartiennent à deux rangées. 

D’où, X + Y + Z = 12.