****************
Solutions
51 à 100
****************
Solution 51. Deux trios
(1, 8, 8) et (2, 5, 10) sont une solution du système d’équations,
car la somme des éléments de chaque trio est la même, soit 17 et celle
des carrés est aussi la même, soit 129. Il est impossible de former un
carré magique formé d’entiers avec les éléments de ces deux trios,
parce que 17 n’est pas divisible par 3. En effet, dans tout carré magique
d’ordre 3, le nombre du milieu est toujours égal au tiers de la somme de
chaque rangée.
En conséquence, un carré magique d’ordre
3 ne donne pas toutes les solutions entières du système d’équations.
Solution 52. Chaque terme est de la
forme (3n + 2). Or, (3n + 2)3 = 27n3
+ 54n2 + 36n + 8. Chaque terme est divisible par 9
sauf 8, qui étant inférieur à 9, devient le reste.
En conséquence, si on divise par 9
le cube de chaque terme de cette suite, le reste est 8.
Solution 53. On rend l’égalité
positive : MAGE + MINE = SEMA. Si E = 3, alors A = 6, à cause des
unités. I ne peut pas être égal à 6, car A = 6. D’où, I = 7 et la
somme G + N est inférieure à 10. Les valeurs possibles de M sont 1, 2 et
4, à cause de la colonne des unités de mille. Comme G + N doit être
inférieure à 10 et qu’il n’y a pas de retenue au-dessus de la colonne
des dizaines, on ne peut pas trouver deux nombres différents (G et N) dont
la somme est 1, 2 ou 4 (M).
En conséquence, E ne peut pas être
égal à 3.
Solution 54. Soit n la base
du plus grand carré, la somme des deux carrés est : (n - 1)2
+ n2 = 2n2 - 2n + 1. La somme des
deux triangulaires est : n(n + 1)/2 + (n + 1)(n
+ 2)/2 = n2 + 2n + 1. On fait : 2n2
- 2n + 1 = n2 + 2n + 1. On obtient : n2
- 4n = 0. D’où, n = 0 et n = 4. On exclut le 0, car
la base du premier carré serait -1.
En conséquence, cette proposition
est vraie seulement pour 32 + 42 = 4D
+ 5D.
Solution 55. Soit une configuration
dont la somme est 13 dans chaque rangée.
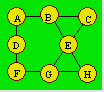
Alors, A + B + C = 13, A + D + F =
13, B + E + H = 13, etc. Pour que tous les éléments apparaissent dans la
deuxième configuration, il faut soustraire de 9 tout élément de la
première. La somme d’une rangée de la deuxième configuration
sera : (9 - A) + (9 - B) + (9 - C). Cela donne : 27 - (A + B + C)
= 27 - 13 = 14. On fait de même avec chacune des autres rangées. On
obtient 14 comme somme dans chaque rangée.
S’il existe au moins une
configuration où la somme est 13, il en existe au moins une dont la somme
est 14.
Solution 56. Sur la première ligne,
on a 1. Au milieu de la deuxième ligne, on aurait 4, le carré de 2. Au
milieu de la troisième ligne, on a 9, le carré de 3. Au milieu de la
quatrième ligne, on aurait 16, le carré de 4. Soit n le rang de la
ligne, le nombre du milieu est (ou serait) n2. Si n
= 4, la somme est : (n2 - 3) + (n2
- 1) + (n2 + 1) + (n2 + 3) = 4n2.
Si n = 5, la somme est : (n2 - 4) + (n2
- 2) + n2 + (n2 + 2) + (n2
+ 4) = 5n2. Le produit du rang de la ligne (ou du nombre
de termes par ligne) et de n2 est n3.
Donc, la somme des nombres de chaque
ligne est un cube.
Solution 57. Soit x et y
les deux nombres, on fait : x + y + x - y +
xy + x/y = x/y(y + 1)2.
On obtient le produit d’une fraction et d’un carré. Il existe
exactement trois carrés à l’exception de 1 qui divisent 675 sans
reste : 9, 25, 225. Si, dans l’intervalle donné, on peut trouver des
valeurs à x et à y, on aura trois couples. Lorsque (y
+ 1)2 est égal à 9, 25 ou 225, y est égal à 2, 4 ou
14. Les seuls couples possibles sont : (2, 150), (4, 108) et (14,
42).
En conséquence, il existe
exactement trois couples de nombres sur lesquels on peut opérer lorsque la
somme des résultats est 675.
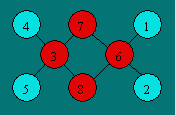
Solution 58. La somme des nombres de
1 à 8 est 36. Comme il y a quatre rangées dont la somme est 15, on
fait : 4 × 15 = 60. Les quatre jetons autres que A, B, C et D
apparaissent deux fois. Leur somme est 24, car 60 - 36 = 24. Comme la somme
totale est 36, on fait : 36 - 24 = 12. Donc, A + B + C + D = 12. Voici
un exemple de configuration :
Solution 59. Chaque boule peut être
associée à 1, 2 et 3. Par exemple, la 4 l’est à 1, la 5 à 2, la 6 à
3, la 7 à 1 et ainsi de suite. On fait comme s’il y avait seulement des
boules numérotées 1, 2 et 3. Il y a dix combinaisons possibles de
trois boules : (1, 1, 1), (1, 1, 2), (1, 1, 3), (1, 2, 2), (1, 2, 3), (1, 3,
3), (2, 2, 2), (2, 2, 3), (2, 3, 3) et (3, 3, 3).
La somme est un multiple de 3 dans
quatre combinaisons sur 10, soit 2/5.
Solution 60. Comme N + G + R = Z et
que les plus petites valeurs possibles de N, G et R sont 1, 2 et 3, la plus
petite valeur de Z est 6. Si Z = 6, alors G = 8, à cause des unités. D’où,
N + R + 8 > 6 : hypothèse à rejeter. Si Z = 7, alors G = 1. On
suppose que N et R valent 2 et 3. Il faudra une retenue de 1 au-dessus de
cette colonne pour que Z soit égal à 7. Les chiffres non utilisés
sont : 0, 4, 5, 6, 8 et 9. On peut faire : E = 6, A = 5 et I = 9.
Il existe au moins une solution lorsque Z = 7.
Donc, la plus petite valeur de Z est
7.
Solution 61. On place les dominos
dans cet ordre en commençant par 1 : (1, a), (a, b), (b, 1),
(1, c), (c, d), (d, 1), (1, e), (e, f). Le demi-domino F ne peut pas être
égal à 1, car les cinq demi-dominos 1 sont posés. On commence par un
demi-domino autre que 1 : (a, 1), (1, b), (b, c), (c, 1), (1, d), (d,
e), (e, 1), (1, f). Le demi-domino F ne peut pas être égal à A, car tous
les dominos sont différents. Dans les deux cas, on ne peut pas accoler le
premier et le dernier domino.
Il est donc impossible de réaliser
une chaîne circulaire avec ces huit dominos.
Solution 62. Dans tout carré
magique d’ordre 3, le médian est égal au tiers de la densité. Soit d
la densité et m le médian, alors m = d/3. On
fait : d - d/3 = 2d/3 : c’est la somme des
éléments extrêmes qui est le double du médian.
En conséquence, dans tout carré
magique d’ordre 3, la somme des éléments extrêmes d’une rangée qui
passe par le centre est le double du médian.
Solution 63. Les termes du milieu
sont : 1, 3, 7, 13, 21, etc. Le terme général est n2
- n + 1. Or, n2 - n est pair, car n2
- n = n(n - 1) qui est le produit de deux entiers
consécutifs. D’où, le nombre du milieu est toujours impair. La somme des
termes également distants du milieu est paire. Un nombre impair plus un
nombre pair donnent un impair.
Donc, la somme des nombres de chaque
ligne est un nombre impair.
Solution 64. La somme des nombres de
1 à 6 est 21. Le total des sommes données est : 6 + 12 + 15 = 33. On
fait : 33 - 21 = 12. La somme du triangle du centre devrait être 12.
Deux triangles dont la somme est 12 auraient alors deux côtés communs. On
devrait avoir le même nombre dans les sommets opposés des deux triangles :
ce qui est impossible, car chaque nombre apparaît une seule fois.
Il est donc impossible de disposer
les nombres de 1 à 6 dans cette figure.
Solution 65. Dans l’addition, il y
a 10 lettres différentes. Il faut donc utiliser les 10 chiffres.
Puisque le 0 ne peut pas être pris,
l’amie a raison d’affirmer qu’il n’existe pas de solution.
Solution 66. Soit un escalier dont
la base exige n cubes. La hauteur exige aussi n cubes. L’escalier
voisin qui lui est plus petit contient (n - 1) cubes, autant pour la
base que pour la hauteur. On fait tourner le petit de 180 degrés et on le
place sur le grand. Chaque côté de la nouvelle figure contient n
cubes. L’aire est n2.
La quantité de cubes nécessaires
pour construire deux escaliers voisins est un carré.
Solution 67. Un nombre de la forme 6n
est un multiple de 6. Un nombre de la forme (6n + 2) ou (6n
+ 4) est un multiple de 2. Un nombre de la forme (6n + 3) est un
multiple de 3. Les nombres de la forme (6n + 1) et (6n + 5) ne
sont pas nécessairement des multiples.
Seuls les nombres de la forme (6n
+ 1) ou (6n + 5) peuvent être des nombres premiers.
Solution 68. Comme 999 est impair, l’un
des entiers devant être élevé au carré est pair et l’autre est impair.
Soit 2m l’un de ces entiers et (2n + 1) l’autre. On
élève au carré chaque entier et on en fait la somme. On obtient 4m2
+ 4n2 + 4n + 1. La somme peut être divisée par 4
avec un reste de 1. Or, si on divise 999 par 4, le reste est 3.
En conséquence, 999 ne peut pas
être la somme de deux carrés.
Solution 69. Dans un carré magique
d’ordre 3, le médian est égal à la moitié de la somme des deux
éléments extrêmes d’une rangée qui passe par le centre. On fait :
(a - 12) + (a + 4) = 2a - 8 et (2a - 8) ¸
2 = a - 4. Le terme du milieu est (a - 4). Dans un carré
magique d’ordre 3, la somme dans chaque rangée est égale au triple du
médian. On fait : 3(a - 4) = 3a - 12. La somme de chaque
rangée est (3a - 12).
En conséquence, la somme de chacune
des rangées est plus petite que 3a.
Solution 70. Les cercles des quatre
coins appartiennent à une seule rangée ; les sept autres
appartiennent à deux rangées. Les nombres de ces sept rangées doivent
être comptés deux fois. Lorsque les quatre coins reçoivent les plus
grands nombres, la somme par rangée est la plus petite possible. On
fait : 2 × (1 + 2 + 3 + 4 + 5 + 6 + 7) + ( 8 + 9 + 10 + 11) = 94 et 94
÷ 6 = 15,67.
Comme 15,67 est la plus petite somme
possible, la somme dans chacune des rangées ne peut pas être 15.
Solution 71. Comme S + A + E = E
(colonne des unités), S + A = 10. Si A = 5, alors S = 5.
Comme chaque lettre représente un
chiffre différent, A ne peut pas être égal à 5.
Solution 72. Le terme général de
la suite 2, 5, 11, 20, 32, ... est (3n2 - 3n +
4)/2. Le terme général de la suite 2, 8, 17, 29, 44, ... est (3n2
+ 3n - 2)/2. Chaque ligne contient une suite arithmétique de n
termes dont le premier et le dernier terme sont connus. Soit A le terme
général de la première suite, Z celui de la deuxième suite et n
le nombre de termes par ligne, on fait : (A + Z)n/2. La somme
est 1,5n3 + 0,5n, soit une fois et demie n3
plus la moitié de n.
En conséquence, la somme des
nombres de chaque ligne est supérieure au cube du rang de la ligne.
Solution 73. La somme des nombres de
1 à 6 est 21. Le total des trois sommes données est 34. On fait : 34
- 21 = 13. La somme des sommets du petit triangle du centre est 13. Deux
sommets sont communs aux triangles de sommes 8 et 13. La différence des
sommes est 5 ; la différence des nombres des deux sommets opposés
devra être 5. Seuls 1 et 6 conviennent. Or, 6 ne peut pas être placé dans
le coin inférieur gauche, car la somme est 8.
Donc, le 6 est toujours dans la
position Y.
Solution 74. Chaque somme est le
produit de deux nombres consécutifs, le premier étant la quantité de
nombres additionnés. Par exemple, on a : 6 = 2 × 3, 12 = 3 × 4, 20 =
4 × 5. Il faut montrer que 654 324 ne peut pas être le produit de deux
nombres consécutifs. On extrait la racine carrée de 654 324 qui est
approximativement 808,9. On fait : 808 × 809 = 653 672, puis 809 ×
810 = 655 290. Le nombre donné est entre ces deux produits.
En conséquence, la somme des
nombres consécutifs pairs à partir de 2 ne peut pas être 654 324.
Solution 75. La somme des nombres de
cette grille est 2551. Il y a un surplus de 551 par rapport à 2000. On doit
exclure trois nombres dont la somme est 551. Le plus petit nombre du tableau
étant 181, on peut, pour simplifier les calculs, soustraire 180 à chacun
des trois nombres exclus. On fait : 3 × 180 = 540 et 551 - 540 = 11. Les
combinaisons de trois nombres dont la somme est 11 sont : (1, 2, 8),
(1, 4, 6), (2, 4, 5). On additionne 180 à chacun des termes des trois
combinaisons et on exclut ces résultats.
En conséquence, il y a trois
façons d’obtenir une somme de 2000.
Solution 76. La somme des nombres de
1 à 8 est 36. On fait 14 × 3 = 42 et 42 - 36 = 6. On devrait placer (1, 5)
et (2, 4) dans les deux cases extrêmes de la rangée horizontale, car ce
sont les seules cases qui appartiennent à deux rangées. Dans les deux cas,
le 8 doit être dans une colonne. On devrait alors compléter chaque colonne
avec 1, 5, 2 ou 4. Or, aucun nombre ne peut être placé deux fois.
Donc, la somme des nombres de chaque
rangée ne peut pas être 14.
Solution 77. Soit n le nombre
de boules dans la rangée du bas, le total des boules est n(n
+ 1)/2. On remplace n par (4m + 1). On a : (4m +
1)(4m + 2)/2 = (4m + 1)(2m + 1). Le produit est un
nombre impair.
En conséquence, le triangle ne peut
pas être partagé en deux parties égales.
Solution 78. La somme des nombres de
1 à 9 est 45. Si la somme par côté était 18, en comptant deux fois
chaque sommet, on ferait : 18 × 3 = 54. La somme des trois sommets
serait 54 - 45 = 9. Les combinaisons possibles de trois nombres dont la
somme est 9 sont : (1, 2, 6), (1, 3, 5), (2, 3, 4). Pour chaque
combinaison, le 9 ne peut pas être placé, car le côté serait complété
par un des nombres du trio.
En conséquence, il est impossible
de disposer les oursons pour que la somme des numéros soit 18 sur chaque
côté.
Solution 79. Soit a = 2002,
on peut écrire : a33 + (a + 3)33 +
(a + 6)33. Quand on élève au carré (a + 3), on
obtient a2 plus des multiples de 3 ou a2
+ M[3]. Si on multiplie cette expression par (a + 3), ce qui revient
à élever (a + 3) au cube, on obtient a3 + M[3].
En multipliant successivement la dernière expression par (a + 3)
jusqu’à la puissance 33, on obtiendra a33 + M[3]. Il en
est de même pour (a + 6). On obtiendra aussi a33 +
M[3]. La somme de a33, de a3 + M[3] et
de a33 + M[3] est 3a3 + M[3]. Les deux
termes de la somme sont des multiples de 3.
D’où, 200233 + 200533
+ 200833 est un multiple de 3.
Solution 80. La somme des nombres de
1 à 9 est 45. Comme il y a quatre rangées, on fait : 4 × 13 = 52,
puis 52 - 45 = 7. Les cellules D, F et H appartiennent chacune à deux
rangées, alors que les autres appartiennent à une seule rangée. La somme
de D, F et H est 7, soit la combinaison (1, 2, 4). La seule valeur possible
de H est 4. Si F = 2, alors D = 1, B = 7 et C + E = 10. Au moins, une des
valeurs qu’on peut attribuer à C ou à E est déjà utilisée. L’hypothèse
est à rejeter. Si F = 1, alors D = 2, B = 8 et C + E = 10. Les seules
valeurs possibles de C et de E sont 3 et 7.
On complète et on obtient la
disposition suivante qui est la seule.
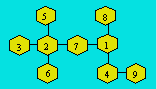
Le 3 et le 7 peuvent être
intervertis, tout comme le 5 et le 6.
Solution 81. On fait : a2
+ (a + 1)2 + c2 = 2a2
+ 2a = 2c. En divisant par 2, on obtient : a2
+ a = c. Pour chaque valeur de a, il existe une valeur
de c. Par exemple, si a = 3, alors b = 4, c = 12
et d = 13. L’égalité est : 32 + 42 +
122 = 132.
Donc, pour chaque valeur de a,
il existe un trio (a, b, c) pour lequel a2
+ b2 + c2 = d2.
Solution 82. Horizontalement, la
somme des nombres est 45, tout comme verticalement. On fait : 119 - 90
= 19 et 121 - 90 = 21. Au centre, comme cette case appartient à quatre
rangées et que deux sont déjà soustraites, on fait : (9 - 1) × 2 =
16. Il y a un surplus de 16 dans le deuxième carré par rapport au premier.
Comme les quatre cases des coins appartiennent à trois rangées et que deux
sont déjà soustraites, on fait : (9 + 8 + 7 + 3) - (1 + 2 + 3 + 7) =
14. Il y a un manque de 14. On fait : 16 - 14 = 2.
En conséquence, la différence des
totaux est 2.
Solution 83. À cause du B de
BATEAU, B = 1. Comme M + B = BA, M = 8 ou 9. Si M = 8, alors A + U ³
10. D’où, A = 0. Pour qu’il y ait une retenue au-dessus de la première
colonne, il faut que U soit égal à 8 ou à 9. Or, M = 8 et A = 0. Comme N
+ N = U, U est pair. L’hypothèse est à rejeter.
En conséquence, M ne peut pas avoir
une valeur inférieure à 9. (En réalité, il n’existe qu’une seule
solution : 90 453 + 16 753 = 107 206.)
Solution 84. Pour trouver chacun des
termes de la suite de Royal, on soustrait 1 à 3n où n
est le rang du jour et on divise le résultat par 2. Le terme général est
(3n - 1)/2. Pour trouver chacun des termes de la suite de
Majesté, on multiplie 3n-1 par 2 et on
soustrait 1. Le terme général est (2 ´ 3n-1
- 1). Les deux termes consécutifs de la suite de Royal sont (3n-1
- 1)/2 et (3n - 1)/2. On additionne ces deux termes. Cela
donne : (3n + 3n-1 -
2)/2. On divise chacun des deux premiers termes par 3n-1.
Cela donne : [3n-1(3
+ 1) - 2] /2, puis (2
´ 3n-1
- 1). Cette dernière expression est le terme général de la suite de
Majesté.
En conséquence, pour n’importe
lequel jour, Majesté recevra autant de billes que Royal pendant ce jour-là
et le précédent.
Solution 85. Comme chaque nombre
intérieur est additionné deux fois, la somme des nombres extérieurs doit
être deux fois celle des nombres intérieurs. Il faut donc que la somme
totale des nombres soit divisible par 3. La somme des nombres de 1 à 10 est
55. Or, 55 n’est pas un multiple de 3.
En conséquence, la tâche est
impossible à réaliser.
Solution 86. Soit n le nombre
de jours travaillés par Rousso, alors Roussi a travaillé (n + 9)
jours. Si n est pair, le carré de n est pair et le carré de
(n + 9) est impair. Le total est un nombre impair. Si n est
impair, le carré de n est impair et le carré de (n + 9) est
pair. Le total est un nombre impair. Or, 1318 est pair.
En conséquence, il est impossible
que les deux écureuils aient cueilli 1318 noix.
Solution 87. Le tableau donne la
répartition des restes possibles de pommes selon les diviseurs.
|
÷ 9 |
÷ 11 |
÷ 13 |
|
0 |
1 |
1 |
|
1 |
0 |
1 |
|
1 |
1 |
0 |
Premier
cas : On fait (11 × 13) + 1 = 144. Le résultat est divisible par 9.
Deuxième
cas : On fait (9 × 13) + 1 = 118. Le résultat n’est pas divisible
par 11.
Troisième
cas : On fait (9 × 11) + 1 = 100. Le résultat n’est pas divisible
par 13.
Seul le premier cas convient. En
conséquence, 144 est la plus petite quantité qui permet un reste de deux
pommes.
Solution 88. A = 0, car E + A = E. S’il
n’y a pas de retenue au-dessus des centaines, M £
10. Il n’y a donc pas de retenue au-dessus de la
colonne des milliers. D’où, I est pair. S’il y a une retenue de 1
au-dessus des centaines, M £
10 et M ne peut pas valoir 0, car A = 0. Il n’y a donc pas de retenue
au-dessus de la colonne des milliers.
D’où, I est pair.
Solution 89. Un carré de n2
points étant donné, on ajoute n points horizontalement, n
points verticalement et un point à l’intersection de ces deux rangées.
La nouvelle figure est formée par (n2 + 2n + 1)
points : c’est le carré de (n + 1). En voici l’illustration :
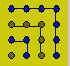
En conséquence, la somme des
nombres impairs consécutifs à partir de 1 est un carré.
Solution 90. Comme il y a cinq
rangées, on fait : 13 × 5 = 65. Sauf la cellule du milieu qui
appartient à trois rangées, chacune des autres appartient à deux
rangées. La somme des chiffres de 1 à 7 est 28. On fait : 2 × 28 =
56, puis 65 - 56 = 9. La cellule du milieu doit recevoir 9. Or, il n’y a
pas de 9.
Donc, la somme dans chaque rangée ne peut pas être 13.
Solution 91. Voici les coordonnées
de chaque point de rencontre des segments :
|
(1, 1) |
(1, 2) |
(1, 3) |
(1, 4) |
(1, 5) |
|
(2, 1) |
(2, 2) |
(2, 3) |
(2, 4) |
(2, 5) |
|
(3, 1) |
(3, 2) |
(3, 3) |
(3, 4) |
(3, 5) |
|
(4, 1) |
(4, 2) |
(4, 3) |
(4, 4) |
(4, 5) |
Lorsqu’on passe d’un brin à l’autre,
les sommes des coordonnées de chaque point passent de pair à impair ou d’impair
à pair. Au départ, la somme des coordonnées est paire et, à l’arrivée,
elle est impaire. Il faut donc passer par un nombre impair de brins. Or, le
nombre (16) de brins devant être atteints par l’araignée est pair.
En conséquence, la recommandation
est impossible à réaliser.
Solution 92. Soit n le rang d’un
terme, le terme général de la suite est 3n + 2. On élève ce
binôme au cube. Le résultat est 27n3 - 54n2
+ 36n - 8. Chacun des trois premiers termes du polynôme est
divisible par 9. Dans ces cas, le reste est 0. Le reste de la division de -
8 par 9 est 1.
En conséquence, le reste de la
division est toujours 1.
Solution 93. Comme il y a le même
nombre d’élèves dans chacune des trois rangées horizontales (ou
verticales), on fait : 108 ÷ 3 = 36. La somme de chaque rangée est
36. On fait : 36 ÷ 3 = 12, car dans tout carré magique d’ordre 3,
le nombre du milieu est égal au tiers de la somme de chaque rangée. On
inscrit 12 au centre. On place 20 dans l’une ou l’autre case libre. La
rangée concernée doit être complétée avec un 4. Or, la balançoire la
moins occupée reçoit cinq élèves.
En conséquence, aucune balançoire
ne peut recevoir plus de 19 élèves. Voici un exemple de répartition des
élèves :
Solution 94. La somme des nombres de
1 à 11 est 66. Comme il y a cinq rangées, on fait : 5 × 17 = 85,
puis 85 - 66 = 19. Quatre boîtes appartiennent chacune à deux
rangées : les trois de la deuxième rangée verticale et celle
marquée A. La somme pour ces quatre boîtes est 19. Or, la somme dans
chaque rangée est 17. On fait : 19 - 17 = 2.
En conséquence, la cellule A ne
peut accueillir que 2. Voici un exemple de configuration :
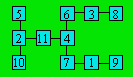
Solution 95. On marque les cases
alternativement avec A et B. Il s’ensuit que les quatre cases amputées
sont marquées A. On compte 9 cases A et 12 B. Chaque domino doit recouvrir
une case A et une B. Comme il y a neuf cases A, on peut théoriquement
déposer au maximum neuf dominos. On vérifie si cela est possible. On a
réussi à agencer neuf couples A et B. Les trois B en blanc ne sont pas
touchés.
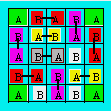
En conséquence, on peut déposer au
maximum neuf dominos sur une grille 5 ´
5 amputée de ses quatre coins.
Solution 96. On pose a, b,
c et d comme étant les termes de chaque rangée du premier
hexagramme. Dans le second hexagramme, la somme des termes d’une même
rangée sera : (2a - 1) + (2b - 1) + (2c - 1) + (2d
- 1) = 2(a + b + c + d) - 4 = 2 ´
26 - 4 = 48.
En conséquence, dans le second
hexagramme, la somme des quatre nombres de chaque rangée est la même.
Solution 97. On colorie les cases
alternativement grises et noires. D’un saut à l’autre, un jeton atteint
toujours une case de même couleur. Or, les deux jetons R sont d’abord sur
des cases grises et à la fin, l’un des deux est sur une case noire.
Il est donc impossible d’obtenir
la figure de droite.
Solution 98. Comme les nombres des
coins appartiennent à deux rangées, la somme des coins P est égale à
trois fois la somme s de chaque rangée diminuée de la somme S des
nombres de 1 à 6. On peut écrire P = 3s - S. Or, 3s est un multiple de 3.
Comme S = 21, S est aussi un multiple de 3. D’où, P est un multiple de
3.
La somme des nombres des coins est
toujours un multiple de 3.
Solution 99.
Le
tableau suivant donne la somme des chiffres pour chaque carré de 1 à 64.
Cette somme a été réduite jusqu’à ce qu’on obtienne un nombre d’un
seul chiffre. Par exemple, pour 49, on fait : 4 + 9 = 13 et 1 + 3 = 4.
|
Carré |
1 |
4 |
9 |
16 |
25 |
36 |
49 |
64 |
|
Somme des chiffres |
1 |
4 |
9 |
7 |
7 |
9 |
4 |
1 |
La somme des chiffres est 1, 4, 7 ou 9. On écrit ces
chiffres dans la colonne de gauche et sur la première ligne ; puis on les
additionne. La partie intérieure comprend les sommes réduites.
|
+ |
1 |
4 |
7 |
9 |
|
1 |
2 |
5 |
8 |
1 |
|
4 |
5 |
8 |
2 |
4 |
|
7 |
8 |
2 |
5 |
7 |
|
9 |
1 |
4 |
7 |
9 |
La somme réduite des chiffres de
7 635 est 3. Or, 3 n’apparaît pas dans le tableau. Il n’est pas
possible que 7 635 soit la somme de deux carrés.
En conséquence, il
est impossible de partager les noix en deux carrés.
Solution 100C. Soit a, a
+ 1, a + 2, a + 3 et a + 4 le nombre de cailloux à la
base et s le nombre de cailloux au sommet, la plus petite valeur de s
est 16a + 19 et la plus grande 16a + 45. Si a = 2, la
plus petite valeur est 51 et la plus grande 77. Or, 88 n’est pas dans cet
intervalle. Si a = 3, la plus petite valeur est 67 et la plus grande
93 : ce qui inclut l’exemple donné. Si a = 4, la plus petite
valeur est 83 et la plus grande 109. On a 88 est dans cet intervalle. On
vérifie si la suite commençant par 4 peut permettre d’atteindre 88 au
sommet. On obtient la configuration suivante :
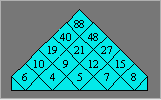
Si a = 5, la plus petite
valeur est 99 et la plus grande 125. Or, 88 n’est pas dans cet
intervalle.
En conséquence, il y a une seule
autre suite d’entiers consécutifs qui permet de disposer 88 cailloux au
sommet.
![]()
![]()