|
Série A
91. Séraphin et son or
Dans un sac d’avoine, Séraphin trouve des pièces de
monnaie en or. Après avoir regardé avec satisfaction ses pièces, il décide
de les assembler. Il dépose d’abord des pièces à la base, puis chaque
pièce est appuyée au centre des deux pièces sous-jacentes. Chaque côté du
triangle illustré contient six pièces.

Séraphin veut placer 250 pièces en un
triangle.
Combien y a-t-il de pièces sur chaque côté
du triangle le plus grand ?
Solution
|
Une
mosaïque est dite d'ordre quinaire si tout
point nodal est le sommet commun de cinq polygones.
|
|
Série B
91. Monnaie de
Cédric
Cédric
prend six pièces de monnaie et les dispose comme ci-après. Il forme ainsi deux
rangées de trois pièces chacune.
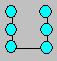
Ajoutez deux pièces de monnaie pour obtenir sept rangées de
trois pièces chacune.
Solution
|
Il
existe une stratégie de résolution de problèmes qui consiste à
utiliser des symboles graphiques.
|
|
Série C
91.
Un rectangle 9 ´ 11
Prenez
trois carrés 1, trois carrés 2, trois carrés 3, deux carrés 4 et un carré
5.
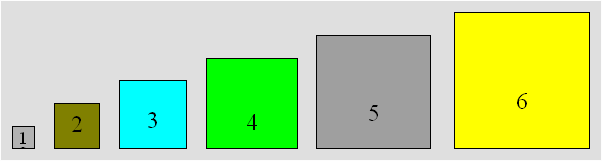
Construisez un rectangle 9 ´
11.
Solution
© Charles-É. Jean
|
Combien
peut-on obtenir de combinaisons de trois nombres différents dont la
somme est 15 avec les nombres de 1 à 11 ?
Solution
|
| |
|
![]()
![]()