|
Série A
Solution 26
Le
nombre total de billes est 70. Par ailleurs, 6 + 14 = 20, 7 + 13 = 20 et 9 + 11
= 20. Le bocal de 10 billes doit être placé à droite, parce qu’il est à l’intersection
de trois tiges. Il doit donc y avoir 30 billes dans chacune des cinq rangées.
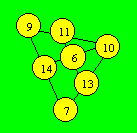
Les combinaisons possibles sont : (6, 10, 14), (6, 11, 13), (7, 9, 14), (7,
10, 13), (9, 10, 11). On complète chaque rangée en respectant les
combinaisons. Une disposition est :
Retour
au problème
|
Solution de l’énigme
On peut
écrire : (22)2 - 2.
|
|
Série B
Solution 26
La boule du centre appartient aux trois
rangées. On y place la boule 7, soit celle du plus grand numéro. On complète
les autres rangées par (1, 6), (2, 5), (3, 4).
La plus
grande somme possible est 14.
Retour
au problème
|
Un
cube coloré est un cube ayant sur
ses faces toutes les combinaisons possibles d'un nombre déterminé de
couleurs.
|
|
Série C
Solution 26
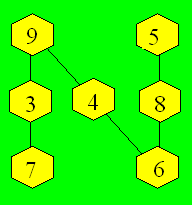
Les combinaisons de trois nombres dont la somme est 19
sont : (3, 7, 9), (4, 6, 9), (4, 7, 8), (5, 6, 8). Une configuration
est :
Retour
au problème
|
Le
mathématicien italien Fibonacci (1175-1240), est surtout connu pour
avoir découvert une suite qui est la solution à un problème de
prolifération de lapins.
|
![]()
![]()