° Nombre étoilé. – Nombre plan qui est représenté sous la forme d'un polygone étoilé. On peut définir deux classes de nombres étoilés : les centrés étoilés et les polygonaux étoilés.

Ö Nombres centrés étoilés
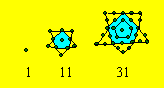
La partie centrale est la représentation d’un nombre centré. Chacune des pointes est formée par un triangle de points dont le nombre de rangées correspond au rang du nombre. Les trois plus petits centrés étoilés pentagonaux peuvent être représentés ainsi :

Le tableau donne huit classes de centrés étoilés et le terme général pour chacune.

Toute raison de la suite des nombres d’un même rang est un hétéromèque. Chaque suite de centrés étoilés d’ordre k est la même que celle des centrés D2 d’ordre 2k. Par exemple, la suite des centrés étoilés pentagonaux est identique à celle des centrés D2 décagonaux. Les centrés étoilés sont des nombres figurés.

Ö Nombres polygonaux étoilés
La partie centrale est la représentation d’un nombre polygonal. Chacune des pointes est formée par un triangle de points dont le nombre de rangées correspond au rang du nombre. Les quatre plus petits étoilés pentagonaux peuvent être représentés ainsi :

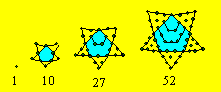
Le tableau donne huit classes de polygonaux étoilés et le terme général pour chacune.

Toute raison de la suite des nombres d’un même rang est un hétéromèque. Chaque suite de polygonaux étoilés d’ordre k est la même que celle des polygonaux d’ordre 2k. Par exemple, la suite des  étoilés pentagonaux est identique à celle des décagonaux. 

Les polygonaux étoilés sont des nombres figurés.

© Charles-É. Jean