Dictionnaire de mathématiques récréatives Nombre centré

Centré
° Nombre centré. – Nombre figuré qui peut être représenté par un ensemble de points disposés de façon régulière sur des figures géométriques. Les classes de dimension inférieure ou égale à 5 sont définies ci-après.

n Nombre centré D1
Nombre centré linéaire ou de dimension 1 dont les points sont disposés sur les côtés d’un polygone régulier. Tout nombre de rang n de cette classe, en exceptant 1, appartient à une suite arithmétique dont le premier terme et la raison sont le nombre de côtés de la figure. Le nombre k de côtés du polygone détermine l’appellation du nombre : triangulaire, carré, pentagonal, etc. Le nombre de points sur chaque côté du polygone détermine le rang n du nombre d’une même classe. Trois centrés polygonaux D1 tous de rang 3 peuvent être représentés ainsi :

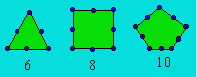
Le centré D1 est représenté par une ligne fermée. Le terme général de rang n, sauf 1, est k(n - 1) où k est le nombre de côtés du polygone. Voici un tableau donnant les 10 plus petits nombres pour huit classes de polygonaux centrés D1 :

Classe/rang n	1	2	3	4	5	6	7	8	9	10	Terme général
Triangulaire	1	3	6	9	12	15	18	21	24	27	3(n - 1)
Carré	1	4	8	12	16	20	24	28	32	36	4(n - 1)
Pentagonal	1	5	10	15	20	25	30	35	40	45	5(n - 1)
Hexagonal	1	6	12	18	24	30	36	42	48	54	6(n - 1)
Heptagonal	1	7	14	21	28	35	42	49	56	63	7(n - 1)
Octogonal	1	8	16	24	32	40	48	56	64	72	8(n - 1)
Ennéagonal	1	9	18	27	36	45	54	63	72	81	9(n - 1)
Décagonal	1	10	20	30	40	50	60	70	80	90	10(n - 1)
Raison	1	1	2	3	4	5	6	7	8	9	n - 1

La suite de ces nombres, en excluant 1, est une suite arithmétique de degré 1.

n Nombre centré D2
Nombre centré plan ou de dimension 2 dont les points sont disposés sur les côtés parallèles de polygones réguliers, ayant en plus un point au centre. Tout nombre de rang n de cette classe est la somme des n plus petits centrés polygonaux D1. Trois polygonaux centrés D2 tous de rang 3 peuvent être représentés ainsi :

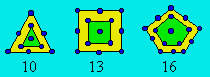
Voici un tableau donnant les 10 plus petits nombres pour huit classes de polygonaux centrés D2 :

Classe/ Rang n	1	2	3	4	5	6	7	8	9	10	Terme général
Triangulaire	1	4	10	19	31	46	64	85	109	136	(3n² - 3n + 2)/2
Carré	1	5	13	25	41	61	85	113	145	181	2n² - 2n + 1
Pentagonal	1	6	16	31	51	76	106	141	181	226	(5n² - 5n + 2)/2
Hexagonal	1	7	19	37	61	91	127	169	217	271	3n² - 3n + 1
Heptagonal	1	8	22	43	71	106	148	197	253	316	(7n² - 7n + 2)/2
Octogonal	1	9	25	49	81	121	169	225	289	361	(2n - 1)²
Ennéagonal	1	10	28	55	91	136	190	253	325	406	(3n - 1)(3n - 2)/2
Décagonal	1	11	31	61	101	151	211	281	361	451	5n² - 5n + 1
Raison	1	1	3	6	10	15	21	28	36	45	n(n - 1)/2

Le terme général de rang n est (kn2 - kn + 2)/2 où k est le nombre de côtés du polygone correspondant. La raison de la suite des nombres de même rang est un triangulaire.

n Nombre centré D3
Nombre centré solide ou de dimension 3 dont les points sont disposés sur un solide associé à un polygone régulier. Tout nombre de rang n de cette classe est la somme des n plus petits polygonaux centrés D2. Voici un tableau donnant les 10 plus petits nombres pour huit classes de polygonaux centrés D3 :

Classe/Rang n	1	2	3	4	5	6	7	8	9	10	Terme général
Triangulaire	1	5	15	34	65	111	175	260	369	505	n(n² + 1)/2
Carré	1	6	19	44	85	146	231	344	489	670	n (2n² + 1)/3 Octaédrique
Pentagonal	1	7	23	54	105	181	287	428	609	835	n (5n² + 1)/6
Hexagonal	1	8	27	64	125	216	343	512	729	1000	n³Cubique
Heptagonal	1	9	31	74	145	251	399	596	849	1165	n (7n² - 1)/6
Octogonal	1	10	35	84	165	286	455	680	969	1330	n(2n + 1)(2n - 1)/3
Ennéagonal	1	11	39	94	185	321	511	764	1089	1495	n(3n² - 1)/2
Décagonal	1	12	43	104	205	356	567	848	1209	1660	n (5n² - 2)/3
Raison	0	1	4	10	20	35	56	84	120	165	n(n - 1)(n + 1)/6

Le terme général de rang n est n(kn² - k + 6)/6 où k est le nombre de côtés du polygone correspondant. La raison de la suite des nombres de même rang est un tétraédrique.

n Nombre centré D4
Nombre centré hypersolide ou solide de dimension 4 dont les points sont disposés sur un hypersolide associé à un polygone régulier. Tout nombre de rang n de cette classe est la somme des n plus petits polygonaux centrés D3. Voici un tableau donnant les 10 plus petits nombres pour huit classes de polygonaux centrés D4 :

Classe/ Rang n	1	2	3	4	5	6	7	8	9	10	Terme général
Triangulaire	1	6	21	55	120	231	406	666	1035	1540	n(n + 1)(n² + n + 2)/8
Carré	1	7	26	70	155	301	532	876	1365	2035	n(n + 1)(n² + n + 1)/6 Hyperoctaédrique
Pentagonal	1	8	31	85	190	371	658	1086	1695	2530	n(n + 1)(5n² + 5n + 2)/24
Hexagonal	1	9	36	100	225	441	784	1296	2025	3025	n²(n + 1)²/4 Hypercubique
Heptagonal	1	10	41	115	260	511	910	1506	2355	3520	n(n + 1)(7n² + 7n - 2)/24
Octogonal	1	11	46	130	295	581	1036	1716	2685	4015	n(n + 1)(2n² + 2n - 1)/6
Ennéagonal	1	12	51	145	330	651	1162	1926	3015	4510	n(n + 1)(3n² + 3n - 2)/8
Décagonal	1	13	56	160	365	721	1288	2136	3345	5005	n(n + 1)(5n² + 5n - 4)/12
Raison	0	1	5	15	35	70	126	210	330	495	n(n - 1)(n + 1)(n + 2)/24

Le terme général de rang n est n(n + 1)(kn² + kn - 2k + 12)/24 où k est le nombre de côtés du polygone correspondant. La raison de la suite des nombres de même rang est un hypertétraédrique.

n Nombre centré D5
Nombre centré solide D5 ou de dimension 5 dont les points sont disposés sur un solide de dimension 5 associé à un polygone régulier. Tout nombre de rang n de cette classe est la somme des n plus petits polygonaux centrés D4. Voici un tableau donnant les 10 plus petits nombres pour huit classes de polygonaux centrés D5 :

Classe/ Rang n	1	2	3	4	5	6	7	8	9	10	Terme général
Triangulaire	1	7	28	83	203	434	840	1506	2541	4081	n(n + 1)(n + 2) (3n² + 6n + 11)/120
Carré	1	8	34	104	259	560	1092	1968	3333	5368	n(n + 1)(n + 2)(n² + 2n + 2)/30 Octaédrique D5
Pentagonal	1	9	40	125	315	686	1344	2430	4125	6655	n(n + 1)³(n + 2)/24
Hexagonal	1	10	46	146	371	812	1596	2892	4917	7942	n(n + 1)(n + 2)(3n² + 6n + 1)/60 Cubique D5
Heptagonal	1	11	52	167	427	938	1848	3354	5709	9229	n(n + 1)(n + 2)(7n² + 14n - 1)/120
Octogonal	1	12	58	188	483	1064	2100	3816	6501	10 516	n(n + 1)(n + 2)(2n² + 4n - 1)/30
Ennéagonal	1	13	64	209	539	1190	2352	4278	7293	11 803	n(n + 1)(n + 2)(9n² + 18n - 7)/120
Décagonal	1	14	70	230	595	1316	2604	4740	8085	13 090	n(n + 1)(n + 2)(n² + 2n - 1)/12
Raison	0	1	6	21	56	126	252	462	792	1287	n(n - 1)(n + 1)(n + 2)(n + 3)/120

Le terme général de rang n est n(n + 1)(n + 2)(kn² + 2kn - 3k + 20)/120 où k est le nombre de côtés du polygone correspondant. La raison de la suite des nombres de même rang est un tétraédrique D5.

Index : C