Rectangulaire

° Nombre rectangulaire. – Nombre plan ou de dimension 2 qui est représenté par un rectangle. On peut classer les rectangulaires selon la différence d entre les mesures entières des côtés du rectangle. Si d = 0, le nombre est carré ; si d = 1, le nombre est hétéromèque ; si d > 1, le nombre est promèque. Le terme général est un polynôme du second degré. 

À l'encontre des polygonaux associés à des figures régulières, un rectangulaire peut avoir plus d'une représentation. Voici les trois représentations de 24, en excluant celle ayant une seule ligne :

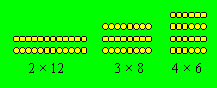
Dans la première figure, d = 10, dans la deuxième d = 5, dans la troisième d = 2. Le nombre 24 est au deuxième rang de classe d = 10, au troisième rang de classe d = 5 et au quatrième rang de classe d = 2. Le tableau suivant contient les 10 plus petits nombres de chaque classe lorsque d varie de 0 à 7.

Les suites de rectangulaires sont des suites arithmétiques de degré 2. Le terme général de rang n est n(n + d). On peut écrire ces suites dans un triangle comme ceci :

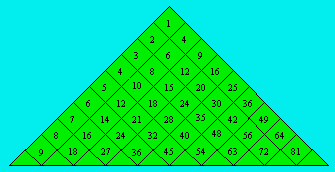
Sur chaque ligne, on trouve une suite de degré 1 dont la différence entre les termes est égale au premier terme de la ligne. Dans les obliques de droite vers la gauche, on trouve des suites arithmétiques de degré 1, dont le premier terme est un carré. Dans les obliques de gauche vers la droite, on trouve des suites arithmétiques de degré 2. Dans la colonne du centre, on trouve les triangulaires de rang impair. Toutes les colonnes contiennent des suites arithmétiques de degré 2. 

Les rectangulaires sont des nombres figurés. 

© Charles-É. Jean