° Nombre promèque. – Nombre  rectangulaire qui est ni carré ni hétéromèque. On peut classer les rectangulaires selon la différence d entre les mesures entières des côtés du rectangle de points. Si d = 0, le nombre est carré ; si d = 1, il est hétéromèque ; si d > 1, il est promèque.

n Promèques d = 2.
On peut trouver la suite des promèques de cette classe, en additionnant successivement 5, 7, 9, 11, 13, 15, ... à partir de 3. Le terme général de rang n est n(n + 2). Les cinq plus petits promèques de cette classe peuvent être représentés ainsi :

Lorsqu’on fait le produit de deux entiers dont la différence est 2, le plus petit entier est le rang du promèque d = 2. Pour trouver son successeur, on lui additionne ses deux rangs suivants. Par exemple, 255 est un promèque de cette classe car 255 = 15 × 17. Il est de rang 15. Son successeur est 255 + (16 + 17) = 288. Les 49 plus petits promèques d = 2 sont :

Voici quelques propriétés des promèques de cette classe :

La période des unités des nombres successifs correspond à deux palindromes successifs : 3 854 583 et 090.

Les unités sont 0, 3, 4, 5, 8 et 9.

La somme des n premiers promèques est égale à n(n + 1)(2n + 7)/6.

La différence de deux promèques successifs est égale à la somme du double du rang du plus grand et de 1.

Si on additionne 1 à un promèque de rang n de cette classe, on obtient un carré de rang (n + 1).

Dans l’intervalle [1, 2499], on trouve trois triangulaires : 15, 120 et 528. D’autres formules peuvent générer les promèques de cette classe : n² - 1, n(n - 2), (n - 1)(n - 3), (n - 4)(n - 2), etc.

n Promèques d = 3.
On peut trouver la suite des promèques de cette classe, en additionnant successivement 6, 8, 10, 12, 14, 16, ... à partir de 4. Le terme général de rang n est n(n + 3). Les cinq plus petits promèques de cette classe peuvent être représentés ainsi :

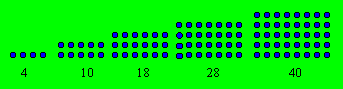
Lorsqu’on fait le produit de deux entiers dont la différence est 3, le plus petit entier est le rang du promèque de cette classe. Pour trouver son successeur, on lui additionne deux fois son rang et 4. Par exemple, 208 est un promèque d = 3 car 208 = 13 × 16. Il est de rang 13. Son successeur est 208 + 2 × 13 + 4 = 238. Les 49 plus petits promèques d = 3 sont :

Voici quelques propriétés des promèques de cette classe :

La période des unités des nombres successifs correspond à deux palindromes : 408 804 et 0880.

Les unités sont 0, 4 et 8.

La somme des n premiers promèques est égale à 2n(n + 1)(n + 5)/6.

La somme d’un promèque de rang n et de (n + 4) est égale à un carré de rang (n + 2).

La différence de deux promèques est égale à la somme du double du rang du plus grand et de 2.

Dans l’intervalle [1, 2548], on trouve quatre triangulaires : 10, 28, 378 et 990. D’autres formules peuvent générer les promèques de cette classe : n(n - 3), (n + 1)(n - 2), (n - 1)(n + 2), (n - 1)(n - 4), etc.

n Promèques d = 4.
On peut trouver la suite des promèques de cette classe, en additionnant successivement 7, 9, 11, 13, 15, ... à partir de 5. Le terme général de rang n est n(n + 4). Les cinq plus petits promèques de cette classe sont représentés ainsi :

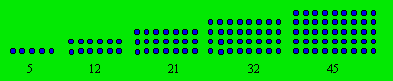
Lorsqu’on fait le produit de deux entiers dont la différence est 4, le plus petit entier est le rang du promèque d = 4. Pour trouver son successeur, on lui additionne deux fois son rang et 5. Par exemple, 252 est un promèque de cette classe car 252 = 14 × 18. Il est de rang 14. Son successeur est 252 + 2 × 14 + 5 = 285. Les 49 plus petits promèques d = 4 sont :

Voici quelques propriétés des promèques de cette classe :

La période des unités des nombres successifs correspond à un nombre de 10 chiffres : 5 212 507 670.

Les unités sont 0, 1, 2, 5, 6 et 7.

La somme des n premiers promèques est égale à n(n + 1)(2n + 13)/6.

Si on additionne 4 à un promèque de rang n de cette classe, on obtient un carré de rang (n + 2).

La différence de deux promèques est égale à la somme du double du rang du plus grand et de 3.

Dans l’intervalle [1, 2597], on trouve quatre triangulaires : 21, 45, 780 et 1596. D’autres formules peuvent générer les promèques de cette classe : n² - 4, n(n - 4), (n - 1)(n + 3), (n - 3)(n + 1), etc.

n Promèques de classe d.
Le terme général de rang n est n(n + d). Les dix plus petits promèques de chaque classe sont : (1+ d), (4 + 2d), (9 + 3d), (16 + 4d), (25 + 5d), (36 + 6d), (49 + 7d), (64 + 8d), (81 + 9d), (100 +10d). On peut trouver la suite des promèques d’une classe en additionnant d et successivement 3, 5, 7, 9, 11, 13, 15, ... à partir de (1 + d). Les suites de nombres promèques sont des suites arithmétiques de degré 2. Les promèques sont des nombres figurés.

© Charles-É. Jean

Index : P