|
Le temps est une préoccupation constante. Au fil des
siècles, différents instruments de mesure sont apparus : le gnomon, le
cadran solaire, la clepsydre (horloge hydraulique), le sablier, les chandelles
graduées, les lampes à l’huile également graduées. La première horloge
mécanique apparaît en Europe au 13e siècle. Elle n’avait qu’une
seule aiguille qui marquait les heures. Au 18e siècle, le
chronomètre est inventé. Par la suite, l’horloge évolue. Elle est à
ressorts, à quartz, puis atomique. Le cadran est muni d’aiguilles ou d’un
affichage numérique. Les montres de poche et les montres bracelets viennent
enrichir la gamme des appareils. Aujourd’hui, on compte un grand nombre d’appareils
électroniques, petits ou non, qui marquent l’heure et qui permettent de
mesurer le temps de certaines opérations.
Nous avons partagé cet article en trois parties : la
mesure du temps, la division du temps et le passage du temps. Nous insisterons
davantage sur la mesure. Nous avons pris soin d’illustrer nos propos par des
récréations en choisissant en grande partie celles d’auteurs anciens.
1. Mesure du temps
1.1 Le sablier
Il peut servir à mesurer une période de temps notamment dans certains jeux
de société. On peut utiliser plus d’un sablier dont le transvasement se fait
par alternance et en des temps différents. Voici une récréation :
Récréation 1. Pour faire cuire un mets qui exige un temps
de six minutes exactement, on a deux sabliers, l’un qui s’écoule en trois
minutes et l’autre en huit minutes. Comment s’y prendra-t-on si on doit
utiliser au moins une fois le plus grand sablier ? (Problème
inédit) Voir solutions
1.2 L’horloge
Le tintement, la disposition des aiguilles, le cadran avec ses chiffres
romains ou arabes, le dateur, la coïncidence d'affichage de chiffres semblables
sont autant d’objets récréatifs. Dans certains cas, ces problèmes peuvent
être adaptés à la montre. Des horloges fantaisistes ont été mises sur le
marché. Les chiffres sont remplacés par des formules, des éléments
périodiques, des expressions mathématiques, etc. Deux tentatives d’horloge
décimale ont été faites l’une en 1793, l’autre en 1897. Le
jour avait une durée de 10 heures. Chaque heure était composée de 100
minutes et chaque minute de 100 secondes. Quand les aiguilles marquaient 10 h,
il était minuit à l’heure conventionnelle ; à 5 heures, il était
midi.
Récréation 2. Je n’ai pas de bracelet-montre, mais
seulement une pendule, et j’ai remarqué tout à l’heure qu’elle s’était
arrêtée. Je me suis donc rendu chez l’un de mes amis pour lui demander l’heure
et, sitôt renseigné, je revins chez moi. Là, je fis un rapide calcul et je
remis ma pendule à l’heure. Lorsque je suis parti, je ne savais pas combien
de temps j’allais mettre pour accomplir le trajet. Comment m’y suis-je donc
pris pour remettre ma pendule à l’heure ? (Problème
posé par Boris Kordiemsky (1907-1999) dans Sur le sentier des mathématiques,
tome 1, Dunod, 1963, p. 36)
Solution 2. En sortant de chez moi, j’avais pensé à
remonter ma pendule, et à noter, d’après elle, l’heure de mon départ. À
mon retour, je pus ainsi déterminer, à partir de ma seule pendule, la durée
de mon absence. En arrivant chez mon ami je notai l’heure indiquée par sa
montre, puis je la notai à nouveau au moment de le quitter. Je connaissais donc
la durée de ma visite chez lui. Ainsi en soustrayant de la durée totale de mon
absence la durée de ma visite chez mon ami, j’obtins le temps employé pour
le trajet aller-retour. Puis, pour déterminer l’heure exacte à laquelle je
devais remettre ma pendule, je n’eus plus qu’à ajouter la moitié du temps
du trajet aller-retour à l’heure indiquée par la montre de mon ami où je l’ai
quitté. (Solution de l’auteur du problème)
Récréation 3. Deux horloges diffèrent au plus de trois
secondes l’une de l’autre. Elles sonnent en même temps une même
heure. Les coups de l’une se produisent toutes les quatre secondes, ceux de l’autre
toutes les cinq secondes. L’oreille confond deux coups s’ils n’interviennent
pas à plus d’une seconde d’écart. Si l’on entend au total treize coups,
quelle heure est-il ? (Problème posé par Pierre Berloquin
dans Le jardin du sphinx, Dunod, 1981, p. 115) Voir
solutions
Récréation 4. La pendule sonne trois heures ; pendant
qu’elle sonne, il se passe trois secondes. Combien de temps la pendule
doit-elle sonner sept heures ? (Problème posé par Yakov
Pérelman (1882-1942) dans Expériences et problèmes récréatifs,
Éditions Mir, 1974, p. 295) Voir
solutions
1.3 Les aiguilles
Sur un cadran de montre ou d’horloge mécanique, trois aiguilles servent à
marquer le temps. L’aiguille des heures, appelée communément petite
aiguille, repose sur 12 divisions significatives qui sont marquées de 1 à 12.
Passé minuit (12 sur le cadran), on dit 0 h jusqu’à 11 h. Passé midi (12
sur le cadran), on dit 12 h jusqu’à 23 h. La première partie du jour
commence aussitôt que l’aiguille des heures dépasse 0 h et se termine à 12
h. La seconde partie du jour commence lorsque l’aiguille des heures dépasse
12 h et se termine à 24 h. L’aiguille des minutes, appelée grande aiguille,
repose sur 60 divisions où elle reçoit une appellation de 0 à 59. Dans la
pratique, on réduit souvent à 12 divisions significatives, chacune
correspondant au multiple de 5 du chiffre inscrit. Par exemple, on dit 14 h et
5, 14 h et 10, 14 h et 15, etc. Le 15, le 30 et le 45 peuvent être remplacés
respectivement par quart, demi et trois quarts (ou moins quart). Dans la partie
gauche de l’horloge, le 7 est dit moins 25, le 8 moins 20, le 10 moins 10 et
le 11 moins 5. Le système d’affichage de l’horloge rend possible des
problèmes récréatifs. Il en est de même du dérèglement du mécanisme qui
amène des retards ou des avances sur l’heure exacte.
Récréation 5. Une horloge possède une aiguille des
secondes. À midi, les trois aiguilles coïncident. Existe-t-il une autre heure,
avant 12 heures, où les trois aiguilles sont exactement superposées ?
(Problème
posé par Martin Gardner (1914-2010) dans "Haha" ou l'éclair de la
compréhension mathématique, Pour la Science, 1979, p. 92) Voir
solutions
Récréation 6. Il y a trois horloges à la maison. Le 1er
janvier, elles marquent toutes l’heure exacte, mais seule la première horloge
fonctionne normalement alors que chaque jour la seconde horloge retarde d’une
minute et la troisième avance d’autant. Si elles continuent à fonctionner
ainsi, dans combien de temps les trois horloges indiqueront-elles à nouveau l’heure
exacte ? (Problème posé par Yakov Pérelman (1882-1942)
dans Expériences et problèmes récréatifs, Éditions Mir, 1974, p.
292) Voir solutions
1.4 Le cadran
Le cadran d’une horloge ou montre mécanique porte
des nombres de 1 à 12 écrits en chiffres arabes ou romains. Dans ce dernier
cas, on trouve parfois IIII au lieu de IV et VIIII au lieu de IX.
Récréation 7. Un cadran affiche des chiffres
arabes.
Partagez le cadran en trois parties de telle manière que les sommes sont
respectivement 22, 23 et 24. (Problème inédit)
Voir
solutions
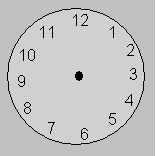
Récréation 8. Le cadran d’une horloge est marqué par des
chiffres romains. Partagez le cadran en quatre parties pour que la somme soit 20
dans chacune des parties. (Problème formulé autrement et
provenant de Boris Kordiemsky (1907-1999) dans Sur le sentier des
mathématiques, tome 1, Dunod, 1963, p. 19) Voir
solutions

1.5 La montre
Les premières montres avaient plutôt un aspect décoratif et étaient
destinées aux femmes. Du temps de Pascal (1623-1662), la montre se portait
déjà au poignet. Toutefois, le premier brevet relatif à la montre-bracelet a
été déposé en 1889. Une grande partie des problèmes récréatifs qui
concernent l’horloge peuvent être appliqués à la montre, selon qu’elle
est à aiguilles ou à affichage numérique.
Récréation 9. Présentez une montre à la personne à qui
vous voulez indiquer l’heure de son lever et priez-la de tourner les aiguilles
de façon à marquer une heure quelconque (cette heure étant représentée par
un nombre entier). Ajoutez mentalement 12 à l’heure indiquée et dites à la
personne de compter les heures une à une jusqu’à la somme que vous avez
obtenue, en prenant pour point de départ l’heure qu’elle a marquée, en se
déplaçant en sens inverse du mouvement, et en commençant à compter à partir
du chiffre indiquant l’heure à laquelle elle désire se lever. La division
sur laquelle elle s’arrêtera est forcément l’heure à laquelle elle
désire se lever. (Problème posé par Bachet de Méziriac
(1581-1638) et mentionné par Gaston Boucheny (1865-1935) dans Curiosités et
récréations mathématiques, Larousse, 1939, p. 85)
Voici un exemple dans lequel on écrit les heures en
chiffres romains : La personne désire se lever à VIII (8) heures et elle
marque V (5) heures sur le cadran. Vous faites 5 + 12 = 17. Sans mentionner l’opération
faite, vous dites à la personne de toucher à V (5) sur le cadran et de compter
les heures jusqu'à 17 dans l’ordre inverse du mouvement des aiguilles. Elle
commence à compter comme si elle était au rang 8, VIII étant l’heure de son
lever. Elle compte 8 (V), 9 (IV), 10 (III), 11 (II), 12 (I), 13(XII), 14 (XI),
15 (X), 16 (IX), 17 (VIII). Au rang 17, on trouve VIII. La personne désire se
lever à 8 heures.
Dans un tour de magie, on peut additionner mentalement un
autre nombre que 12. Dans ce cas, lors de l’arrêt, on corrigera mentalement l’opération
de comptage et on dira à la personne : " Non, ce n’est pas ton
heure de lever, c’est plutôt ... ". On peut remplacer les aiguilles
par des objets numérotés comme des cartes ou encore on peut choisir une autre
suite.
Récréation 10. Une montre retarde d’un quart de minute
pendant le jour mais, par suite du changement de température, elle avance d’un
tiers de minute pendant la nuit. Au bout de combien de jours aura-t-elle avancé
de 2 minutes, sachant qu’aujourd’hui, au soir, elle donnait l’heure
exacte ? (Problème posé par Gaston Boucheny (1865-1935)
dans Curiosités et récréations mathématiques, Larousse, 1939 p. 81) Voir
solutions
Récréation 11. Une personne regarde sa montre entre
3 h et 4
h, puis entre 6 h et 7 h. Chacune des deux aiguilles ayant pris la place de l’autre,
quelle heure était-il exactement à chacune des observations de la
montre ? (Problème posé par Gaston Boucheny (1865-1935)
dans Curiosités et récréations mathématiques, Larousse, 1939, p. 84) Voir
solutions
Récréation 12. Il y a 3 heures et demie, j’ai remis à l’heure
mon réveil qui retarde de 4 minutes par heure. Il est actuellement midi à ma
montre, qui, elle, fonctionne parfaitement. Dans combien de minutes le réveil
indiquera-t-il lui aussi midi ? (Problème posé par Boris
Kordiemsky (1907-1999) dans Sur le sentier des mathématiques, tome 1,
Dunod, 1963, p. 41) Voir
solutions
Récréation 13. Sur un cadran à affichage numérique, la
différence entre les heures et les minutes est la même qu’entre les minutes
et les secondes. La somme des trois marques est 54. La marque des secondes est
une fois et demie celle des secondes. Quelle heure est-il ? (Problème
inédit) Voir solutions
Récréation 14. Quand Andrée est arrivée au travail, il
était 13 : 27. Quand elle a quitté le travail, les quatre mêmes chiffres
apparaissaient sur sa montre. Pendant combien de temps au minimum André
a-t-elle travaillé ? (Problème inédit) Voir
solutions
1.6 L’âge
L’âge est la mesure de la vie d’une personne ou d’un bien. Les
problèmes consistent à déterminer l'âge d'une ou de plusieurs personnes à
partir d'informations précises. Le temps écoulé depuis la naissance peut
être mis en relation avec les chiffres qui la déterminent. L’épitaphe de
Diophante est un exemple de problème sur l’âge. Nicolas Boileau (1636-1711)
a écrit le texte suivant intitulé Le bilan de la vie humaine dans
lequel il répartit les tâches d’une personne qui aura vécu 95 ans. (Texte
cité par Étienne Ducret (1829-1909) dans Divertissements mathématiques,
Garnier, 1980, p. 88)
L'Homme, dont la vie entière
Est de
quatre-vingt-quinze ans,
Dort le tiers de sa
carrière ;
C'est juste
trente-deux ans
32
Ajoutons, pour
maladie,
Procès, voyage,
accidents,
Au moins un quart de
sa vie :
C'est encor deux fois
douze ans 24
Par jour, deux heures
d'étude
Ou de travaux font
huit ans
8
Noirs chagrins,
inquiétudes,
Pour le double font
seize ans 16
Pour l'affaire qu'on
projette
Demi-heure, encor
deux ans 2
Cinq quarts d'heure
de toilette,
Barbe et cætera :
cinq ans
5
Par jour, pour manger
et boire,
Deux heures font bien
huit ans 8
Cela porte le
mémoire
Jusqu'à
quatre-vingt-quinze ans 95
Récréation 15. Le texte suivant apparaît sur l’épitaphe
du maréchal Maurice de Saxe (1696-1750).
Son courage l'a fait
admirer de chac
1
Il eut des ennemis,
mais il triompha
2
Les rois qu'il
défendit sont au nombre de
3
Pour Louis son grand
coeur se serait mis en
4
Des victoires par an
il gagna plus de
5
Il fut fort comme
Hercule et beau comme Tir 6
Pleurez, braves
soldats, ce grand homme hic ja 7
Il mourut en novembre
et de ce mois le
8
Strasbourg contient
son corps en un tombeau tout 9
Pour tant de Te
Deum, pas un de profun
10
Quel âge avait le maréchal de Saxe quand il est
décédé ? (Problème cité par Étienne Ducret (1829-1909)
dans Divertissements mathématiques, Garnier, 1980, p. 87) Voir
solutions
Gaston Boucheny (1865 -1935) a donné une façon de deviner l’âge
d’une personne et le mois de sa naissance.
Récréation 16.
Demandez à une personne d’effectuer les opérations suivantes.
1e
Multiplier le numéro du mois de sa naissance par 2.
2e Au
résultat, ajouter 5.
3e
Multiplier le nouveau résultat par 50.
4e Au
produit obtenu, ajouter l’âge puis, de la somme, retrancher 365.
5e
Demander le résultat obtenu et lui ajouter mentalement 115.
On obtient ainsi un nombre de 3 ou 4 chiffres, le chiffre des
mille et des centaines est le numéro du mois de la naissance, les deux autres
forment le nombre qui constitue l’âge. (Devinette formulée
autrement et provenant de Curiosités et récréations mathématiques,
Larousse, 1939, p. 86)
Solution 16. Par exemple, une personne est née en mars et a
42 ans. La personne fait : 3 ´ 2 = 6, 6 + 5 =
11, 11 ´ 50 = 550, 550 + 32 = 582, 582 - 365 = 217.
Le résultat de la personne est 217. On fait mentalement 217 + 115 = 342. Le 3
correspond à mars et 42 est l’âge.
Récréation 17. -
Non monsieur, je regrette mais je ne puis vous accorder la main de ma fille.
Elle est beaucoup trop jeune (16 ans) et vous avez trois fois son âge. Vous
pourriez largement être son père ? !
- Mais Monsieur si au
lieu du triple de son âge, j’en avais le double, m’accorderiez-vous sa
main ?
- Ah ! Dans ce
cas, je ne dirais pas non.
- Bien ! Alors
Monsieur j’attendrai.
Combien de temps
attendra-t-il ? (Problème posé par Maurice Denis Papin
dans Colles et astuces mathématiques, Blanchard, 1972, p. 64) Voir
solutions
Récréation 18. Le grand-père, la grand-mère, le père, la
mère et l’enfant ont chacun 20 ans de plus que l’autre. Leurs âges réunis
forment 250 ans. Quel est l’âge de chacun des cinq membres de cette honorable
famille ? (Problème posé par Étienne Ducret dans Divertissements
mathématiques, Garnier, 1980, p. 56) Voir
solutions
Récréation 19. Mon
histoire s’est passée en 1982. J’avais alors exactement l’âge donné par
les deux derniers chiffres de ma date de naissance. Lorsque j’en ai fait la
remarque à mon grand-père, il m’a bien étonné en déclarant qu’il en
était de même pour lui. Cela m’a paru impossible ...
- C’est impossible,
bien entendu, dit une voix.
- Eh bien non, c’est
tout à fait possible, et mon grand-père me l’a prouvé. Quel était l’âge
de chacun d’entre nous ? (Problème posé par Yakov
Perelman (1882-1942) dans Oh, les maths !, Éditions Mir, 1992, p.
18) Voir solutions
Récréation 20. Un père, interrogé sur l’âge
de son fils, répond : Mon âge est triple de celui de mon fils et, il y a
dix ans, il était le quintuple. Quel est l’âge du fils ? (Problème
posé par Joseph Bertrand (1822-1900) dans Traité d’arithmétique,
Hachette, 1863, p. 227) Voir
solutions
2. Division du temps
Le temps est partagé en millénaires, siècles, années, jours,
heures, secondes, cette dernière étant l’unité de base.
2.1 Le calendrier
Les principaux problèmes ont trait au jour de la semaine d'une date
donnée, aux années bissextiles et au temps écoulé entre deux dates. La
disposition des quantièmes sur le calendrier de même que les millésimes
permettent aussi des récréations. À la fin du 20e siècle, les
chiffres des années se prêtaient bien à une récréation qu’on appelait problème
de l’année. Il s’agissait de faire diverses opérations sur les quatre
chiffres pour arriver à des résultats compris dans un intervalle donné.
Récréation 21. Combinez les chiffres de 1982 au moyen d’opérations
pour que les résultats varient de 1 à 16. (Problème inédit)
Voir solutions
2.2 Les heures
Situer le temps dans un jour se fait principalement par les heures. On peut
penser à l’heure sur l’horloge et à la différence d’heures entre deux
moments déterminés.
Récréation 22. Quelle heure est-il ? demandait un
quidam à Pythagore. "Il reste encore de la journée (24 heures) deux
fois les deux tiers de ce qui est déjà écoulé.", lui répondit le
philosophe. (Problème posé par Émile Fourrey dans Récréations
mathématiques, Vuibert, 1947, p. 151) Voir
solutions
2.3 Le jour de la semaine
De nombreux auteurs ont établi des tableaux ou des formules qui permettent
de trouver à peu près sans calcul le jour de la semaine d’une date donnée
ou, inversement, la date relative à un événement qui se produit à un jour
fixe d'une semaine donnée. Citons les auteurs comme Bakst,
Chang, Comstock,
Delambre,
Devi, Fourrey,
Gauss, Keith-Craver,
Kraitchik, Lucas,
Moret, Ore,
Roy, Walsh et
Zeller. On désigne généralement ces outils comme étant un
calendrier perpétuel.
Récréation 23. Quel jour de la semaine l’année a-t-elle
commencé si le 24 juin est un jeudi ? (Problème posé dans
Arithmétique, cours supérieur, FEC, 1907, no 1329) Voir
solutions
Récréation 24. Le 1er janvier de l’année 1978
tombait un dimanche. Dans ces conditions, que se passera-t-il pour le siècle à
venir et, d’une manière générale, quelle probabilité ont les siècles du
calendrier grégorien de commencer par un dimanche ? (Problème
posé par Pierre Berloquin dans Le jardin du sphinx, Dunod, 1981, p. 131)
Voir solutions
3. Passage du temps
3.1 Les fêtes communes
Certaines fêtent tombent un jour de la semaine donné ; d’autres
sont prévues à des dates précises. Par exemple, Friedrich Gauss et T. H. O’Beirne
ont établi des formules pour déterminer la date annuelle de Pâques. Ces
fêtes sont souvent des prétextes pour imaginer des problèmes. La première
récréation ci-après est reliée à la fête de Noël, la seconde à Pâques.
Récréation 25. En été, trois personnes fêtent le même
jour leurs anniversaires. Leurs jours de naissance sont tombés trois jours
différents et consécutifs de la semaine. Le 1er janvier 1969, le
produit des âges des trois personnes était égal à 70 840. Quel jour de la
semaine est tombé le premier Noël de la personne la plus âgée ? (Problème
posé par J. C. Baillif dans Les casse-tête logiques de Baillif, Dunod,
1979, p. 6) Voir solutions
Récréation 26. L’épicier du village a disposé sur un
rayon 21 œufs de Pâques, alignés l’un à côté de l’autre. Une cliente
entre à 9 heures précises, réfléchit une minute et dit : "Je
prends le premier à gauche." Elle paie et s’en va. Aussitôt, une
deuxième cliente entre, réfléchit deux minutes et dit : "Je
prends le deuxième de gauche." Même jeu avec une troisième cliente
qui entre aussitôt, réfléchit trois minutes et prend le troisième de gauche.
Et ainsi de suite avec les clientes suivantes. Compte tenu du fait que l’emballage
et les opérations de caisse durent une minute exactement pour chaque cliente,
à quelle heure la cliente qui partira avec l’œuf situé à l’extrême
droite quittera-t-elle l’épicerie ? (Problème posé par
Jean-Claude Paquet dans Les nouvelles énigmes du prof Jissé, La Presse,
1986, p. 29) Voir solutions
3.2 Les anniversaires
On s’intéresse notamment au temps écoulé depuis une date précise jusqu’à
un anniversaire, au jour de la semaine d’un anniversaire ou au taux de
probabilités que deux personnes ou plus dans un groupe aient la même date de
naissance.
Récréation 27. Gaston est né un lundi 18 mars 1991. Il
aimerait bien fêter son 18e anniversaire de naissance un lundi.
Croyez-vous que son rêve est possible ? (Problème inédit)
Voir solutions
3.3 Les retrouvailles
Les principaux problèmes touchent à des personnes ou des mobiles qui se
rencontrent en un même endroit.
Récréation 28. Notre école compte cinq clubs qui
fonctionnent au temps donné : plomberie (un jour sur 2), menuiserie (un jour
sur 3), photo (un jour sur 4), échecs (1 jour sur 5) et chant choral (un jour
sur 6). Les cinq clubs se sont réunis le 1er janvier d’une année
ordinaire, puis aux intervalles prévus. Combien y a-t-il eu de soirées durant
le premier trimestre où aucun des clubs ne s’est réuni ? (Problème
formulé autrement et provenant de Yakov Perelman (1882-1942) dans Oh, les
maths !, Éditions Mir, 1992, p. 16) Voir
solutions
3.4 Les tâches
Le temps consacré à des tâches peut faire l’objet de récréations
variées. Dans le problème de la tour de Brahma, on veut connaître le temps
nécessaire pour transférer les 64 disques d'une aiguille à une autre. Le
problème de l’escargot qui veut sortir du puits, en montant et en descendant
par périodes, a été souvent imité.
Récréation 29.
Martin se souvient du jour où il a réussi son premier gâteau. Il se souvient
même de l’heure où il a ouvert le four et a senti l’odeur de cette petite
merveille.
Le quantième est
supérieur de 11 à la marque de l’heure.
Les minutes sont le
triple de l’heure.
Le quantième est le
triple de celui du mois.
Tous les chiffres
sont différents.
Quand Martin a-t-il
réussi son premier gâteau ? On demande la date et l’heure. (Problème
inédit)
Voir
solutions
Récréation 30. Une cuve est munie de 3 robinets ; si
on les ouvre tous les trois, elle se vide en 2 heures ; si on ouvre
seulement les deux premiers, elle se vide en 2 h ¾. Trouver le temps qu’il
faudrait au troisième robinet pour vider seul la cuve. (Problème
posé dans Arithmétique, cours supérieur, FEC, 1907, no 1030)
Voir
solutions
3.5 Les déplacements
Quand on met en relation un espace parcouru et le temps, on introduit la
notion de vitesse.
Récréation 31. Jeannot met 2 heures pour descendre la
rivière et 3 heures pour faire le trajet de retour en ramant à la même
allure. Combien de temps aurait-il mis pour couvrir la même distance à la
même allure sur un lac ? (Problème posé par J. C. Baillif
dans Les casse-tête logiques de Baillif, Dunod, 1979, p. 49) Voir
solutions
Récréation 32. Deux trains partent, l’un de A avec une
vitesse de 50 milles à l’heure, l’autre de B avec une vitesse de 40 milles,
et vont à la rencontre l’un de l’autre. À quelle distance de A se
croiseront-ils, si la distance AB est de 270 miles ? (Problème
tiré de Mathématiques de la vie courante, cours supérieur, FEC,
1948, p. 486) Voir solutions
Curieuse façon de voyager, tel est le titre de la
récréation suivante.
Récréation 33. Deux personnes n’ont qu’une seule
bicyclette pour faire un parcours de 20 km. La première part sur la bicyclette
à la vitesse de 15 km à l’heure, en même temps que la deuxième part à
pied à la vitesse de 4,5 km à l’heure. Après un certain trajet, la
première personne laisse la bicyclette sur le talus de la route et termine le
parcours à pied à la vitesse de 5 km à l’heure. La deuxième personne
trouve la bicyclette et termine avec elle le parcours à la vitesse de 12 km à
l’heure ; les deux personnes arrivent en même temps à destination.
Calculer la distance du point de départ à l’endroit où la machine a été
abandonnée et la durée totale du trajet. (Problème posé par
Gaston Boucheny (1865-1935) dans Curiosités et récréations mathématiques,
Larousse, 1939 p. 77) Voir
solutions
Plus spécifiquement, on peut allier le temps à la vitesse
par le biais de sonneries d’horloge comme dans cet exemple.
Récréation 34. Deux horloges électriques, A et B, sont
placées aux deux extrémités d’une rue longue de 1960 verges. L’horloge A
commence de sonner 3 secondes avant l’horloge B. Quel est le point de la rue
où l’on entend les deux horloges sonner en même temps, sachant que le son
parcourt 372 verges à la seconde ? (Problème tiré de Arithmétique,
cours supérieur, FEC, 1907, no 348) Voir
solutions
Conclusion
Nous avons montré que le temps peut être associé à de nombreuses
récréations. La mesure du temps se fait notamment par des objets mécaniques.
La division du temps permet d’établir des relations entre différents
moments. Plusieurs situations de la vie courante peuvent être converties en
problèmes récréatifs. Les 34 problèmes laissent voir un reflet des
possibilités. Û
*******************
Solutions
Solution 1. §
On
renverse les deux sabliers (état 1 ci-après). Au bout de trois minutes, la
partie supérieure du petit est vide. Il reste cinq minutes à l’autre (état
2).
§ On renverse le
petit (état 3). Au bout de trois minutes, la partie supérieure de l’autre
marque deux minutes et l’inférieure six minutes (état 4).
§ On renverse le
grand. On commence alors la cuisson qui exige six minutes.
Le tableau illustre les états successifs des deux sabliers.
S désigne la partie supérieure et I la partie inférieure.
|
États |
|
0 |
1 |
2 |
3 |
4 |
|
Sablier de
3 minutes |
S
I |
0
3 |
3
0 |
0
3 |
3
0 |
0
3 |
|
Sablier de
8 minutes |
S
I |
0
8 |
5
3 |
5
3 |
5
3 |
2
6 |
Solution 3. Il est 9 heures.
Solution 4. La pendule sonne sept heures pendant neuf
secondes.
Solution 5. Les trois aiguilles ne sont superposées
exactement qu’à 12 heures.
Solution 6. Dans 720 jours. Pendant ce temps, la seconde
horloge retardera de 720 minutes c’est-à-dire 12 heures ; la troisième
avancera d’autant. Les trois horloges indiqueront alors la même heure que le
1er janvier, c’est-à-dire l’heure exacte.
(Solution de l’auteur du problème)
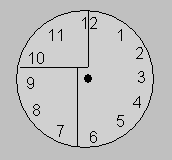
Solution 7. La somme des nombres de 1 à 12 est 78. La somme
des trois parties est 69. Il y a un écart de 9 entre les deux sommes. Comme 12
- 3 = 9, on tire un trait entre le 1 et le 2 de 12. Voici une façon de partager
le cadran :
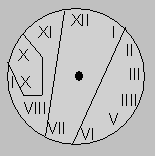
Solution 8. Voici le partage suggéré par l’auteur du
problème :
Solution 10. La montre mettra 20 jours plus la durée d’une
nuit.
Solution 11. Il était d’abord 3 h 31 min 28 s, puis 6 h 18
min 20 s.
Solution 12. En 3 heures et demie, le réveil prend 14
minutes de retard. À midi, il indiquera donc 11 h 46. Il lui reste encore 14
minutes avant midi, au cours desquelles il retardera presque d’une minute
supplémentaire. C’est donc dans presque 15 minutes que le réveil indiquera
midi. (Solution de l’auteur du problème)
Solution 13. Comme la somme des trois marques est 54, celle
des minutes est 54/3 = 18. La marque des secondes est 27 et celle des heures est
9. Il est 9 : 18 : 27.
Solution 14. La prochaine heure est 21 : 37. Andrée a
travaillé pendant huit heures et 10 minutes.
Solution 15. On fait la somme des chiffres qui termine chaque
phrase. La somme est 55. Le maréchal de Saxe est décédé à 55 ans.
Solution 17. Au bout de 16 ans, la fille aura 32 ans et lui
aura 64 ans. Il devra attendre 16 ans.
Solution 18. Le grand-père a 90, la grand-mère 70, le père
50, la mère 30 et l’enfant 10 ans.
Solution 19. Le petit-fils est né en 1941 et le grand-père
en 1891. En 1982, le petit-fils avait 41 ans et le grand-père 91 ans.
Solution 20. Le fils a 20 ans.
Solution 21. Un exemple est donné dans chaque cas.
|
8 + 2 - 1 ´ 9 = 1 |
9 + 2 - 1 - 8 = 2 |
1 ´ 9 - 8 + 2 = 3 |
9 - 8 + 1 + 2 = 4 |
|
1 ´ 9 - 8/2 = 5 |
8 ´ 2 - 1 - 9 = 6 |
8 ´ 2 - 1 ´
9 = 7 |
8 ´ 2 + 1 - 9 = 8 |
|
9 ´ 2 - 1 - 8 = 9 |
9 ´ 2 - 1 ´
8 = 10 |
9 ´ 2 + 1 - 8 = 11 |
8 ´ 2 - 1 - Ö
9 = 12 |
|
8 ´ 2 - 1 ´
Ö 9 = 13 |
8 ´ 2 + 1 - Ö
9 = 14 |
8 + 9 - 1 ´ 2 = 15 |
8 + 9 + 1 - 2 = 16 |
Solution 22. Il est 10 heures et 17 minutes.
Solution 23. L’année
a commencé un vendredi.
Solution 24. Un siècle ne commence jamais un dimanche.
Solution 25. La personne la plus âgée est née en 1912. Son
premier Noël, le 25 décembre 1912, fut un mercredi.
Solution 26. La dernière cliente sortira de l’épicerie à
10 : 17.
Solution 27. Son rêve ne se réalisera pas car le 18 mars
2009 est un mercredi.
Solution 28. Il y eut 23 soirées sans réunion de
clubs : 8 en janvier, 7 en février et 8 en mars.
Solution 29. L’événement est arrivé le 27 septembre (9)
à 16 h 48 min.
Solution 30. En 1 h, les 3 robinets vident ½ de la cuve, et
les deux premiers les 4/11. En 1 h, le 3e robinet vide ½ - 4/11 =
8/22 de la cuve. (Solution de l’auteur du problème)
Solution 31. Il aurait fallu 4 h 48 min pour faire le même
trajet à la même allure sur un lac.
Solution 32. Les deux trains se croiseront à 150 milles de
A.
Solution 33. La distance du point de départ à l’endroit
où la machine a été abandonnée est de 8,57 km et la durée totale du trajet
est de 2 h 51 min 25 s.
Solution 34. Le son de l’horloge A aura parcouru 3 fois 372
ver. ou 1116 ver. quand l’horloge B sonnera. C’est donc au milieu de l’espace
restant que l’on entendra en même temps le son des deux horloges. On fait
(1960 - 1116) ¸
2 = 422. Le point commun est à 422
ver. de l’horloge B et à 1538 ver. de l’horloge A. (Solution
de l’auteur du problème)
|
|
![]()
![]()