Icosaèdre

Polyèdre à 20 faces. L'icosaèdre régulier a 12 sommets et 30 arêtes ; ses faces sont des triangles équilatéraux. Voici un  patron qui permet de construire un icosaèdre :

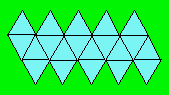
Un minimum de cinq bandes sont nécessaires pour natter un icosaèdre. L'icosaèdre peut être tronqué. Le tableau suivant contient les 10 plus petits nombres pour chacune des classes de nombres figurés reliés à l'icosaèdre. La dimension D est donnée pour chaque classe.

© Charles-É. Jean