|
Multiplication
° Table de multiplication.
– Tableau
de nombres obtenus par la multiplication de deux entiers, l'un
étant placé en abscisse et l'autre en ordonnée. Cette table présente les
produits de 1 à 9.
|
× |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
1 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
2 |
2 |
4 |
6 |
8 |
10 |
12 |
14 |
16 |
18 |
|
3 |
3 |
6 |
9 |
12 |
15 |
18 |
21 |
24 |
27 |
|
4 |
4 |
8 |
12 |
16 |
20 |
24 |
28 |
32 |
36 |
|
5 |
5 |
10 |
15 |
20 |
25 |
30 |
35 |
40 |
45 |
|
6 |
6 |
12 |
18 |
24 |
30 |
36 |
42 |
48 |
54 |
|
7 |
7 |
14 |
21 |
28 |
35 |
42 |
49 |
56 |
63 |
|
8 |
8 |
16 |
24 |
32 |
40 |
48 |
56 |
64 |
72 |
|
9 |
9 |
18 |
27 |
36 |
45 |
54 |
63 |
72 |
81 |
Le produit est placé à l’intersection d’un nombre de la
colonne de gauche et d’un nombre de la ligne supérieure. Chaque rangée
horizontale ou verticale de la table contient une suite arithmétique
de degré
1 dont chaque terme est un multiple du premier nombre. La diagonale
descendante contient la suite des
carrés. L’autre diagonale contient une suite arithmétique finie de degré 2
qui commence par 9, qui se termine par 25 et dont la différence entre les termes
est décroissante. Voici une deuxième façon de représenter une
table de multiplication :
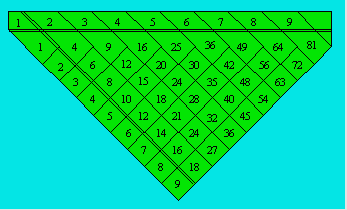
Le produit est à l’intersection d’un nombre de la
première oblique et d’un nombre de la première ligne. Par exemple, pour
trouver le produit de 5 et de 8, on lit 8 dans la première oblique et 5 sur la
première ligne. La suite des carrés apparaît sur la ligne commençant par 1.
Sur la ligne commençant par 2, on trouve les nombres hétéromèques ; sur
la ligne commençant 3, les nombres promèques de la classe d = 2 ;
sur la ligne commençant par 4, les nombres promèques de la classe d =
3 ; sur la ligne commençant par 5, les nombres promèques de la classe d
= 4 et ainsi de suite. Voici une troisième façon de représenter une table de
multiplication :

On trouve le produit à l’intersection des deux
obliques extérieures portant chacun de ces nombres. La rangée verticale
centrale est formée par les carrés consécutifs. Chaque rangée oblique
contient une suite arithmétique de degré 1 dont chaque terme est un multiple
du premier nombre de la rangée. À partir de la ligne 5, chaque ligne contient
une suite finie de degré 2 qui se termine dans la rangée verticale centrale ou
dans la précédente et dont la différence entre les termes est décroissante.
Chaque rangée verticale contient une suite infinie de degré 2. On peut
partager une table de multiplication en gnomons, en retenant seulement les
produits.
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
2 |
4 |
6 |
8 |
10 |
12 |
14 |
16 |
18 |
|
3 |
6 |
9 |
12 |
15 |
18 |
21 |
24 |
27 |
|
4 |
8 |
12 |
16 |
20 |
24 |
28 |
32 |
36 |
|
5 |
10 |
15 |
20 |
25 |
30 |
35 |
40 |
45 |
|
6 |
12 |
18 |
24 |
30 |
36 |
42 |
48 |
54 |
|
7 |
14 |
21 |
28 |
35 |
42 |
49 |
56 |
63 |
|
8 |
16 |
24 |
32 |
40 |
48 |
56 |
64 |
72 |
|
9 |
18 |
27 |
36 |
45 |
54 |
63 |
72 |
81 |
n Chacun des nombres placés
dans le coin inférieur droit d’un gnomon est un carré dont la racine
correspond au rang du gnomon. Par exemple, 36 est dans le sixième gnomon.
n La somme des nombre de chaque
gnomon est un cube dont la base est le plus petit nombre du gnomon. Par exemple,
2 + 4 + 2 = 8 = 23, 3 + 6 + 9 + 6 + 3 = 27 = 33, 4 + 8 +
12 + 16 + 12 + 8 + 4 = 64 = 43.
n La somme des nombres de
chaque carré incluant tous les gnomons à partir de 1 est un carré parfait
dont la base est un nombre triangulaire. Par exemple, 1 + 2 + 3 + 4 + 2 + 4 + 6
+ 8 + 3 + 6 + 9 + 12 + 4 + 8 + 12 + 16 = 100 = 102 = (1 + 2 + 3 + 4)2.
De ces deux dernières propositions, on peut déduire que 13 + 23
+ 33 + ... + n3 = (1 + 2 + 3 + ... + n)2.
Cette identité était connue dans l’Antiquité.
La table de multiplication est une table de Pythagore.
© Charles-É. Jean
Index
: M
|
![]()
![]()