|
Semi-régulière
°
Mosaïque
semi-régulière. – Mosaïque formée de deux ou de plusieurs types
de polygones réguliers, dans laquelle on retrouve le même nombre de polygones
différents et la même séquence de figures autour du point nodal.
Il existe
huit mosaïques semi-régulières : six constitués de deux types de polygones
réguliers et deux constitués de trois types de polygones réguliers. Trois
mosaïques sont d'ordre ternaire, deux d'ordre quaternaire et trois d'ordre
quinaire. Elles résultent de combinaisons variées de triangles, de carrés,
d'hexagones, d'octogones et de dodécagones, tous étant des polygones
réguliers.
|
Polygones à chaque point nodal |
Code |
Ordre |
|
Trois triangles et deux carrés |
(3, 3, 3, 4, 4) |
Quinaire |
|
Trois triangles et deux carrés |
(3, 3, 4, 3, 4) |
Quinaire |
|
Quatre triangles et un hexagone |
(3, 3, 3, 3, 6) |
Quinaire |
|
Un triangle, deux carrés et un hexagone |
(3, 4, 6, 4) |
Quaternaire |
|
Deux triangles et deux hexagones |
(3, 6, 3, 6) |
Quaternaire |
|
Un carré et deux octogones |
(4, 8, 8) |
Ternaire |
|
Un triangle et deux dodécagones |
(3, 12, 12) |
Ternaire |
|
Un carré, un hexagone et un dodécagone |
(4, 6, 12) |
Ternaire |
Voici la base de six mosaïques semi-régulières :
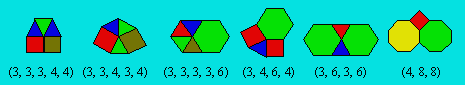
© Charles-É. Jean
Index
: S
|
La mosaïque
semi-régulière est aussi appelée mosaïque homogène.
|
![]()
![]()