****************
Récréations 1 à 50
****************

Ce recueil contient 100 récréations pour lesquelles il faut établir un algorithme. Rappelons qu’un algorithme est un ensemble d’instructions présentées dans un ordre déterminé et permettant d’atteindre le résultat demandé.

À titre d’exemple, un algorithme qui permet de trouver la somme des entiers consécutifs à partir de 1 jusqu’à un entier donné pourrait s’énoncer ainsi :

Un entier étant donné,
100. On additionne 1.
110. On multiplie par l’entier donné.
120. On divise par 2.

Le résultat est la somme des entiers consécutifs à partir de 1 jusqu’au nombre donné. Par exemple, si l’entier donné est 5, on fait : 5 + 1 = 6, 6 × 5 = 30, puis 30 ÷ 2 = 15. La somme des entiers de 1 à 5 est 15.

Pour chaque récréation, un algorithme est suggéré. Il n’est pas le seul possible.

Amusez-vous bien.

* * * * * * * * * * * * * * * *

1. Médaillons de Magalie
Magalie a une collection de médaillons. Elle les place sur les murs de sa chambre. La première rangée contient sept médaillons. La deuxième rangée est formée de 10 médaillons. Chaque rangée successive contient trois médaillons de plus que la précédente.

Trouvez un algorithme qui permet de déterminer le nombre de médaillons pour une rangée donnée.

2. Pommes de Sofia
Sofia achète un sac de 24 pommes. Le premier jour, elle donne deux pommes. À chaque jour suivant, elle donne deux pommes jusqu’au 12^e jour où elle distribue ses deux dernières pommes.

Trouvez un algorithme qui permet de déterminer le nombre de pommes qui lui restent en un jour de rang donné.

3. Allumettes d’Isabelle
Isabelle représente la figure ci-après avec des allumettes. Elle continue selon le même modèle en ajoutant une case d’une rangée horizontale à une autre.

Trouvez un algorithme qui permet de déterminer le nombre d’allumettes qui seront requises pour représenter une figure dont le rang de la dernière rangée horizontale est donné.

4. Coccinelles de Cédric
À chaque année, depuis l’âge de 10 ans, Cédric calcule le tiers de son âge. Quand le résultat est un entier, il dessine une coccinelle.

Trouvez un algorithme qui permet de déterminer le nombre de coccinelles dessinées de l’âge de 10 ans jusqu’à un âge donné.

5. Multiples de Zénon
Zénon fait la somme des multiples consécutifs de 3. Il écrit :

Le plus grand multiple à additionner étant donné, trouvez un algorithme qui permet de déterminer la somme des nombres sur cette ligne.

6. Fruits de Luc
Luc entreprend de grouper deux à deux les lettres de son prénom. Il a trouvé les trois groupes : (L, U), (L, C), (U, C). Pour chacun des groupes, sa mère lui donne deux petits fruits.

Trouvez un algorithme qui permet de déterminer le nombre de fruits qu’un enfant pourrait recevoir dans les mêmes conditions, étant connu son prénom.

7. Grilles de Mathias
Mathias trace une grille carrée et noircit deux cases par ligne et deux cases par colonne. Voici un exemple dans une grille 4 × 4 :

Trouvez un algorithme qui permet de déterminer le nombre de cases non noircies dans une grille carrée dont le nombre de lignes ou de colonnes est connu.

8. Lapinières d’Élise
Élise a préparé trois enclos pour ses lapins. Un bon jour, elle compte 23 lapins dans les enclos A et B, puis 18 lapins dans les enclos B et C.

Trouvez un algorithme qui permet de déterminer le nombre total de lapins quand le nombre de l’enclos B est connu.

9. Monnaie de Daphnée
Daphnée a disposé des pièces de monnaie dans des tableaux qui contiennent chacun trois rangées horizontales. D’un tableau à l’autre, elle ajoute une colonne. Les trois premiers tableaux sont donnés ci-après. En passant par six pièces, Daphnée trace des rectangles.

Trouvez un algorithme qui permet de déterminer le nombre de rectangles qui passent par six pièces dans une grille dont le nombre de colonnes est donné.

10. Opérations de Livia
Livia choisit un nombre. Elle le multiplie par 2, puis additionne 3. Elle continue en multipliant par 2 et en additionnant 3 successivement.

Trouvez un algorithme qui permet de déterminer le 10^e nombre de la séquence quand Livia choisit un nombre arbitrairement.

11. Points d’Armand
Armand dessine des points sur le contour d’hexagones. Sur chaque côté, il place le même nombre de points, dont un à chaque sommet. Voici un exemple quand l’hexagone a quatre points par côté.

Trouvez un algorithme qui permet de déterminer le nombre de points requis pour un hexagone dont le nombre de points par côté est connu.

12. Veille de vacances
Dans une classe, il y a quatre filles de plus que de garçons. Chaque garçon va au tableau et écrit deux fois le mot CONGÉ. Chaque fille va au tableau et écrit trois fois le mot CONGÉ.

Trouvez un algorithme qui permet de déterminer le nombre de fois où CONGÉ aura été écrit si un nombre quelconque de garçons est donné.

13. Perles d’Éric
Éric fait toujours ses courses le samedi. Le premier samedi, il achète huit perles et en donne deux. Le deuxième samedi, il en achète 10 et en donne trois. Par la suite, d’un samedi à l’autre, il achète deux perles de plus et en donne une de plus.

Trouvez un algorithme qui permet de déterminer le nombre total de perles qui appartiendront à Éric après les courses d’un samedi de rang donné.

14. Fourmis de Marius
Marius a dressé des fourmis. Avant d’aller à l’école, il leur demande de se placer en rangées. La première rangée doit contenir 10 fourmis et chaque rangée successive contient trois fourmis de plus que la précédente.

Trouvez un algorithme qui permet de déterminer le nombre de fourmis dans une rangée donnée.

15. Lapins de Mathis
Mathis distribue des lapins aux habitants de deux villages. Au village A, il donne trois lapins à chaque maison. Au village B, il donne cinq lapins à chaque maison. Il y a quatre maisons de plus au village B qu’au village A.

Trouvez un algorithme qui permet de déterminer le nombre de lapins qui auront été distribués quand le nombre total des maisons des deux villages est connu.

16. Pyramide de Sara
Sara a préparé la pyramide ci-après. Tout nombre appartenant à une ligne supérieure est égal à la somme de deux nombres inférieurs adjacents. Par exemple, 3 + 4 = 7.

Trouvez un algorithme qui permet de déterminer le nombre supérieur de la pyramide si le premier nombre de la ligne inférieure est donné et si les quatre nombres de cette ligne sont consécutifs de façon croissante.

17. Craies de Coralie
Coralie place une craie sur la table. Par la suite, chacun de ses élèves devra y déposer deux craies. Chaque fois qu’un élève a fait son dépôt, Coralie et ses élèves vérifient si les craies pourraient être partagées également entre trois élèves. Si oui, un des élèves a la tâche de dessiner un cœur.

Trouvez un algorithme qui permet de déterminer la quantité de craies sur la table en fonction du nombre donné de cœurs dessinés.

18. Oiseaux de Vincent
Vincent dessine deux oiseaux en une première colonne. Par la suite, il dessine successivement trois oiseaux par colonne.

Un nombre d’oiseaux étant donné, trouvez un algorithme qui permet de déterminer dans quelle colonne se trouve l’oiseau qui correspond au rang du nombre.

19. Alphabet de Julien
Julien écrit les lettres de l’alphabet selon le modèle ci-après. D’un groupe à l’autre, il augmente d’une lettre en respectant toujours l’ordre alphabétique à partir de A.

Trouvez un algorithme qui permet de déterminer le nombre de lettres écrites depuis le début jusqu’à la dernière lettre d’un groupe donné.

20. Un couple numérique
Stella choisit un nombre. Elle le multiplie par 3. Zack prend le nombre qui est supérieur de 5 à celui choisi par Stella. Il le multiplie par 2. Au résultat de Stella, il additionne le sien.

Trouvez un algorithme qui permet de déterminer le résultat final de Zack en fonction du nombre pris par lui.

21. Sacs de nectarines
Trois amies ont acheté des nectarines.
Aimée a trois nectarines de plus que Bianca.
Bianca a une nectarine de moins que Karine.

Trouvez un algorithme qui permet de déterminer le nombre total de nectarines en fonction de ce que Karine possède.

22. Ficelles de Mathias
Mathias représente des grilles carrées avec des ficelles de même longueur. Il compte le nombre de ficelles requises pour former la partie intérieure. Par exemple, dans cette grille 3 × 3, Mathias aura besoin de 12 ficelles à l’intérieur.

Trouvez un algorithme qui permet de déterminer le nombre de ficelles nécessaires pour former la partie intérieure d’une grille carrée donnée.

23. Noisettes de Catherine
Catherine distribue des noisettes à ses trois filles. La deuxième reçoit trois noisettes de plus que la première. La troisième reçoit cinq noisettes de plus que la deuxième.

Trouvez un algorithme qui permet de déterminer le nombre total de noisettes distribuées en fonction de ce que la première fille reçoit.

24. Légumes de Philippe
Dans son petit marché d’alimentation, Philippe vend des légumes. La première semaine, il a vendu 12 sacs de navets, la deuxième semaine 10 sacs, la troisième semaine 13 sacs, la quatrième semaine 11 sacs. Les ventes se poursuivent selon le même rythme, soit alternativement deux sacs de moins et trois sacs de plus d’une semaine à l’autre.

Trouvez un algorithme qui permet de déterminer le nombre de sacs vendus pour une semaine donnée.

25. Roman d’Alexis.
Alexis est en train d’écrire un roman. Il a déjà 100 pages d’écrites. Son intention est de ne pas dépasser 300 pages. Il s’interroge sur le nombre de chiffres qui seront nécessaires pour paginer son roman.

Un nombre de pages étant atteint dans l’intervalle donné, trouvez un algorithme qui permet de déterminer le nombre de chiffres requis pour la pagination de son roman.

26. Cases grisées
Lina prépare trois grilles : une 3 × 3, une 4 × 4 et une 5 × 5. Dans la première grille, elle grise une case par ligne et par colonne ; dans la deuxième grille, deux cases par ligne et par colonne ; dans la troisième grille, trois cases par ligne et par colonne. Elle colorie d’autres grilles selon la même régularité.

Trouvez un algorithme qui permet de déterminer le nombre de cases grises dans une grille carrée donnée.

27. Animaux de Benjamin
Benjamin collectionne les timbres qui représentent des animaux de la forêt. Il les conserve dans un cahier spécial de 20 pages. Sur la première page, il dépose cinq timbres. Sur chaque page suivante, il place trois timbres de plus que sur la précédente.

Trouvez un algorithme qui permet de déterminer le nombre total de timbres à partir de la première page jusqu’à une page donnée.

28. Tableau d’Arnaud
Arnaud a préparé le tableau ci-après. Il y a écrit les entiers impairs à partir de 1 selon une certaine régularité en ajoutant des colonnes au besoin.

Trouvez un algorithme qui permet de déterminer le nombre de la troisième ligne dans une colonne de rang donné.

29. Oranges de Pauline
Pauline a acheté un panier d’oranges. Elle partage le panier en deux parts égales entre ses deux filles Alice et Lili. L’une d’elles donne deux oranges à son frère et partage ce qui lui reste en parts égales à l’intention de ses trois amies.

Trouvez un algorithme qui permet de déterminer le nombre d’oranges du panier si on connaît le nombre d’oranges reçues par l’une ou l’autre des amies.

30. Impairs de Marilou
Marilou dispose les entiers impairs consécutif en un triangle comme ci-après. D’une ligne à l’autre, elle écrit un nombre de plus.

Trouvez un algorithme qui permet de déterminer le dernier entier d’une ligne donnée.

31. Lapinière d’Alain
Alain forme des rangées de 2, 3, 4, 5, ... lapins en ajoutant un lapin d’une rangée à l’autre. Il compte le nombre de lapins dans les deux premières rangées (regroupement 1), dans les trois premières rangées (regroupement 2), dans les quatre premières rangées (regroupement 3) et ainsi de suite.

Trouvez un algorithme qui permet de déterminer le nombre de lapins dans un regroupement donné.

32. Diagonales d’Élodie
Élodie a préparé la figure suivante. Par la suite, elle trace une diagonale dans chaque petit carré. Puis elle compte le nombre de triangles dans chaque rangée horizontale.

Trouvez un algorithme qui permet de déterminer le nombre de triangles depuis la première rangée supérieure jusqu’à une rangée de rang donné.

33. Pommes des champs
Trois cousins sont allés ramasser des pommes de terre. Félix a cueilli trois fois plus de sacs que Daniel. Nicolas a cueilli 10 sacs de plus que Félix.

Trouvez un algorithme qui permet de déterminer le nombre total de sacs de pommes de terre ramassées quand on connaît le nombre de sacs de Daniel.

34. Monnaie de Béatrice
Béatrice a disposé des pièces de monnaie comme ci-après. La figure formée de cinq rangées horizontales contient 2, 3, 4, 5 et 4 pièces. Béatrice produit d’autres figures en ajoutant successivement une pièce par rangée.

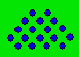
Trouvez un algorithme qui permet de déterminer le nombre de pièces de monnaie requises pour une figure de rang donné.

35. Macarons de Jérémie
Jérémie a placé ses macarons dans trois boîtes. Dans la boîte B, il y a neuf macarons de plus que dans la A. Dans la boîte C, il y a cinq macarons de plus que dans la B.

Trouvez un algorithme qui permet de déterminer le nombre total de macarons quand on connaît le nombre de macarons de la boîte A.

36. Escalier de Maxime
Maxime a préparé le tableau ci-après. Il y a écrit les entiers consécutifs en ajoutant deux nombres d’une ligne à l’autre. Il désire continuer à écrire les entiers selon le même modèle.

Trouvez un algorithme qui permet de déterminer le nombre du milieu d’une ligne donnée.

37. Roman de Claudia
Aujourd’hui dimanche, Claudia se délasse en commençant la lecture d’un roman. Le lundi suivant, elle lit deux fois plus de pages que le dimanche. Le mardi, elle lit 12 pages de moins que le lundi. Le mercredi, elle termine son roman en lisant la moitié moins de pages que le mardi.

Trouvez un algorithme qui permet de déterminer le nombre de pages du roman lorsque le nombre de pages lues le mercredi est donné.

38. Produits de William
William fait la multiplication des entiers consécutifs. Par exemple, il écrit :

1 × 2 = 2

1 × 2 × 3 = 6

1 × 2 × 3 × 4 = 24

1 × 2 × 3 × 4 × 5 = 120

Parvenu au multiplicateur 5, il réalise que le produit se termine par un 0. Il continue alors de faire des multiplications selon la même régularité.

Trouvez un algorithme qui permet de déterminer le nombre de zéros qui terminent le produit quand le plus grand multiplicateur est donné.

39. Achats d’oranges
Trois amies Clara, Luce et Marie achètent des oranges dans des sacs qui normalement ont la même quantité de ce fruit.

• Clara et Luce ont acheté ensemble quatre sacs.

• Luce et Marie ont acheté ensemble trois sacs ; mais il manque cinq oranges.

• Clara et Marie ont acheté cinq sacs ; mais il manque 11 oranges.

Trouvez un algorithme qui permet de déterminer le nombre total d’oranges achetées par les trois amies lorsque le nombre normal d’oranges par sac est donné.

40. Choix de Mélanie
Mélanie choisit un premier nombre. Elle fait deux opérations successives. Pour tout autre nombre choisi, elle fait les mêmes opérations. Par exemple, si elle choisit 12, le résultat est 38 ; si elle choisit 14, le résultat est 44 ; si elle choisit 16, le résultat est 50.

Trouvez un algorithme qui permet de déterminer le résultat si le nombre choisi est connu.

41. Croix de Noémie
Noémie a formé les deux figures ci-après avec des cure-dents. Par la suite, elle ajoute une colonne au milieu de chaque figure.

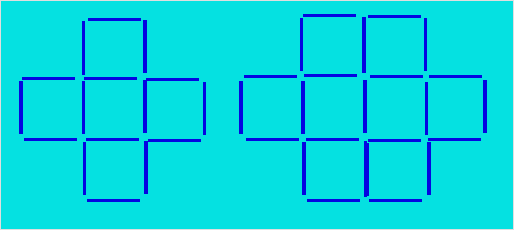
Trouvez un algorithme qui permet de déterminer le nombre de cure-dents requis pour une figure de rang donné.

42. Dîner à l’école
On ne connaît pas le nombre de tables de la cafétéria de l’école Cinq-Étoiles. Lors d’un dîner, deux tables sont occupées chacune par quatre élèves. Trois tables sont occupées chacune par cinq élèves. Les autres tables sont occupées chacune par six élèves.

Trouvez un algorithme qui permet de déterminer le nombre d’élèves présents si le nombre de tables est connu.

43. Tableau de Geneviève
Geneviève a préparé le tableau ci-après. Elle a écrit les entiers consécutifs à partir de 1 en serpentant et en ajoutant des colonnes au besoin. Elle numérote les colonnes formées de trois nombres.

Trouvez un algorithme qui permet de déterminer le nombre de la troisième ligne d’une colonne de trois nombres dont le rang est donné.

44. Cortège de fourmis
Cinq fourmis d’une première fourmilière partent en pèlerinage. À la fourmilière suivante, sept fourmis joignent le cortège. Par la suite, le nombre de fourmis augmente toujours de sept d’une fourmilière à l’autre.

Trouvez un algorithme qui permet de déterminer le nombre total de fourmis qui forment le cortège pour un nombre donné de fourmilières atteintes.

45. Tableau de Lucienne
Lucienne a préparé le tableau ci-après. À partir de 1, chaque nombre est augmenté de 3.

Trouvez un algorithme qui permet de déterminer combien de nombres inférieurs à un nombre donné sont divisibles par 5.

46. Une excursion
Dans un camp de vacances, un certain nombre d’enfants partent en excursion. Après avoir collectionné des feuilles d’arbres, la monitrice les fait asseoir en cercle à l’orée de la forêt. À tour de rôle, chaque enfant se lève et distribue quatre feuilles à chacun des autres enfants.

Trouvez un algorithme qui permet de déterminer le nombre total de feuilles qui seront distribuées pour un nombre donné d’enfants.

47. Cubes de Jason
Jason fait l’addition d’entiers impairs consécutifs comme ci-après. Il réalise que le résultat est toujours un cube. Il continue à faire des additions selon le même modèle.

1 = 1

3 + 5 = 8

7 + 9 + 11 = 27

13 + 15 + 17 + 19 = 64

21 + 23 + 25 + 27 + 29 = 125

Trouvez un algorithme qui permet de déterminer le premier élément d’une ligne donnée.

48. Billes multiples
A met 1, 2, 3 billes dans un sac.

B met 1, 2, 3, 4, 5, 6 billes dans un sac.

C met 1, 2, 3, 4, 5, ... jusqu’à 9 billes dans un sac.

D met 1, 2, 3, 4, 5, ... jusqu’à 12 billes dans un sac.

Chaque personnage suivant E, F, G, ... met des billes dans un sac selon la même régularité.

Trouvez un algorithme qui permet de déterminer le nombre de billes pour n’importe quel personnage.

49. Tableau de Ludovic
Ludovic a préparé le tableau ci-après dans lequel il a écrit les entiers impairs consécutifs.

Trouvez un algorithme qui permet de déterminer le produit des deux nombres d’une colonne de rang donné.

50. Pyramide de Christophe
Christophe construit une pyramide de cubes. Dans l’exemple donné, il place six cubes à la base, quatre cubes pour former la deuxième rangée et deux cubes pour la rangée supérieure. Christophe construit d’autres pyramides en ayant soin de placer un nombre pair de cubes à la base.

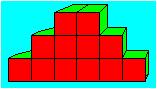
Trouvez un algorithme qui permet de déterminer le nombre de cubes requis pour former une pyramide dont le nombre de cubes à la base est donné.