Dictionnaire de mathématiques récréatives Carré latin régulier

Régulier

° Carré latin régulier. – Carré latin d’ordre n qui appartient à un ensemble de carrés latins formés selon une même règle. Voici quatre classes de carrés latins réguliers :

1. Il existe 12 carrés latins réguliers d'ordre 4 dans lesquels les éléments sont dans le même ordre cyclique sur chaque ligne. En voici quatre où sur chaque ligne l’on trouve v, £, µ et L dans l'ordre cyclique :

v

£

µ

L

L

v

£

µ

µ

L

v

£

£

µ

L

v

L

v

£

µ

v

£

µ

L

L

v

£

µ

L

v

£

µ

µ

L

v

£

µ

L

v

£

v

£

µ

L

µ

L

v

£

£

µ

L

v

£

µ

L

v

£

µ

L

v

v

£

µ

L

2. Les six carrés latins suivants reçoivent les quatre éléments différents dans chacun des quatre carrés 2 ´ 2 des coins et dans le carré 2 ´ 2 central.

1

2

4

3

1

2

4

3

1

2

4

3

1

2

4

3

1

2

4

3

1

2

4

3

3

4

1

2

4

3

2

1

3

4

2

1

4

3

1

2

3

4

2

1

3

4

2

1

4

3

2

1

3

4

1

2

4

3

1

2

3

4

2

1

2

3

1

4

4

1

3

2

2

1

3

4

2

1

3

4

2

1

3

4

2

1

3

4

4

1

3

2

2

3

1

4

3. Dans les quatre carrés latins ci-dessous, la première ligne et la première colonne sont respectivement identiques d'un carré à l'autre.

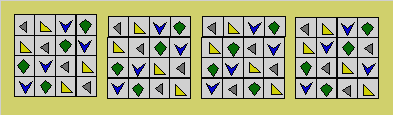
On peut construire des motifs à partir de carrés latins. Voici un motif correspondant respectivement à chacun des quatre carrés latins précédents :

4. Les deux carrés latins suivants d’ordre 6 sont composés de six rectangles chacun contenant les nombres de 1 à 6.

1	2	3	4	5	6	1	2	3	4	5	6
6	5	4	3	2	1	4	5	6	1	2	3
2	3	1	5	6	4	3	1	2	6	4	5
5	4	6	2	1	3	6	4	5	3	1	2
3	1	2	6	4	5	2	3	1	5	6	4
4	6	5	1	3	2	5	6	4	2	3	1

Le sudoku appartient à cette classe. Le carré latin régulier appartient à la classe des récréations combinatoires.

Index : R

Voir :

Carré latin antidiagonal

Carré gréco-latin

Carré latin diagonal

Carré latin inextensible

Carré latin normalisé

Carré latin orthogonal

Carré latin pandiagonal

Carré latin symétrique