Solutions 61 à 70
61. Tour d’Arielle

Arielle déplace la tour sur un échiquier. Elle sait que cette pièce se déplace horizontalement et verticalement, mais jamais en diagonale. Il y a, dans la grille, deux cases noires qu’il faut éviter.

En partant de la case 1 et en avançant d’une case à la fois, trouvez un chemin permet d’atteindre toutes les cases une et une seule fois.

62. Prénom de Lucas

Lucas a écrit les lettres de son prénom dans la grille. Dix lettres sont en bonne position.

Complétez la grille pour qu’il y ait des lettres différentes dans chaque ligne, colonne et diagonale.

63. Marche d’un girafon

Un girafon part de la case 1 sur la grille ci-après. Il se déplace en deux mouvements qui se font en alternance. Le premier mouvement est le saut du cavalier aux échecs, soit en L. Le suivant est un pas horizontalement ou verticalement. Les cinq premières cases atteintes sont indiquées. À la suite de la cinquième case, le girafon doit passer par toutes les autres cases, sauf par les deux noires.

Trouvez un chemin possible.

64. Triple cavalier

Jeannette place un cavalier sur chacune des cases marquées C de la grille ci-après. Comme aux échecs, le cavalier se déplace en L. Chaque cavalier saute sur les cases qu’il lui est possible d’atteindre toujours à partir d’une case C.

Si on exclut les cases C, combien de cases ne pourront pas être atteintes par les cavaliers ?

65. Cartes de Marjo

Marjo dessine une grille 3 × 3. Elle retire neuf pièces d’un jeu de cartes :

• 3, 4 et 5 de cœur

• 4, 5 et 6 de pique

• 5, 6 et 7 de trèfle

Elle place deux cartes comme ci-dessous.

Placez les autres cartes pour que la somme des chiffres soit 15 dans chaque rangée horizontale, verticale et diagonale. De plus, il doit y avoir une seule couleur (cœur, pique ou trèfle) dans chaque rangée horizontale et verticale.

66. Triangle d’Anita

Anita a dessiné le triangle ci-après. Elle a écrit 1, 2 et 3 dans les angles. Il lui faut placer chacun des nombres de 4 à 9 dans les cases pour que la somme soit 17 sur chaque côté du triangle.

Trouvez une façon de distribuer les nombres de 4 à 9 dans les cases.

67. Cases de Lucie

Dans le tableau ci-après, Lucie veut disposer les nombres de 3 à 10 dans les cases pâles. La somme dans chaque rangée diagonale de trois cases doit être 20. Lucie a déjà placé le 10.

Complétez le tableau.

68. Trios de Philippe

Philippe dispose 15 jetons numérotés de 1 à 15 comme ci-après. Il prend trois jetons à la fois, un dans chacune des trois rangées horizontales. La somme des deux jetons des deux premières rangées doit être égale au numéro du jeton de la troisième rangée. Philippe a formé tous les trios possibles lorsque la somme des trois jetons est 24.

Combien y a-t-il de trios possibles ?

69. Grille de Fred

Dans une grille 4 × 4, Fred écrit certaines lettres de son prénom comme ci-après. Il veut compléter la grille avec les mêmes lettres de façon que les quatre lettres apparaissent dans chaque rangée horizontale et dans chaque rangée verticale.

Complétez la grille.

70. Billes de Naomie

Naomie a caché ses billes dans neuf cases disposées en un carré. Son petit frère a dérobé les billes de sept cases. Les deux cases non touchées ont 6 et 3 billes comme il est montré. Naomie sait qu'il y avait exactement 15 billes dans chaque rangée horizontale, verticale et diagonale.

Combien y avait-il de billes dans chacune des sept cases avant l'intervention du petit frère ?

                                                                                                                                Solutions 71 à 80

71. Monnaie de Marjo

Marjo a disposé 16 plateaux en un carré comme ci-après. Elle a placé quatre pièces de monnaie.

Ajoutez quatre pièces de monnaie de façon qu’il y ait deux pièces dans chaque rangée horizontale, verticale et diagonale.

72. Magie de Gabrielle

Gabrielle a dessiné la figure ci-après. Elle veut placer six nombres parmi les entiers de de 1 à 8. La somme doit être 9 dans chaque rangée horizontale et verticale de deux ou de trois cases accolées.

Disposez six nombres.

73. Collation d’Anna

Pendant la collation, Anna a préparé une grille 5 × 5. Elle y écrit 10 chiffres.

Complétez la grille avec des chiffres de 1 à 5 pour qu’il y ait un chiffre différent dans chaque rangée horizontale, verticale et diagonale.

74. Cercles magiques

Jacob a dessiné quatre cercles et y a placé neuf cellules. Il veut placer chacun des nombres de 1 à 10, sauf 4. La somme des nombres sur chaque cercle doit être 17. Le 9 et le 10 sont en bonne position.

Distribuez les autres nombres.

75. Oranges de Gino

Gino a numéroté huit oranges de 2 à 9. Il a placé deux oranges, la 3 et la 6, dans la grille ci-après. Il veut disposer les autres oranges dans les autres cases pâles de façon que la somme des numéros soit 17 dans chacune des quatre diagonales.

Distribuez les six autres oranges.

76. Repos de Johanne

Johanne se repose en voulant compléter le tableau ci-après. Il s’agit d’y placer les nombres de 2 à 8. La somme dans chaque rangée horizontale, verticale et diagonale de deux ou de trois cases, pas nécessairement accolées, doit être 12. Le 1 est déjà en bonne place.

Complétez le tableau.

77. Le A d’Alice

Alice a dessiné un A sur lequel elle a dessiné des cercles. Elle découpe six jetons et les numérote de 1 à 6. Elle place le jeton 6 sur le cercle du haut.

Placez les autres jetons sur les cercles de façon que la somme des numéros soit 11 dans chacune des trois rangées reliées par une droite.

78. Tableau de Céline

Dans le tableau ci-après, Céline veut placer les nombres de 1 à 7. La somme dans chaque rangée horizontale, verticale et diagonale de trois cases doit être 12. Céline a déjà placé le 2 dans une case.

Complétez le tableau.

79. Billes de Jérôme

Dans un sac, Jérôme dépose 2 billes bleues, 3 rouges et 4 noires. Il s’amuse à former des groupes de 3 billes de couleurs différentes.

Combien y a-t-il de combinaisons de trois billes dont l’une est bleue, l’autre est rouge et la troisième est noire ?

80. Magie de Samantha

Samantha a écrit les nombres de 1 à 25 dans la grille ci-après. Elle a effacé 13 nombres. La somme des nombres de chaque ligne, chaque colonne et chaque diagonale doit être 65.

Complétez la grille avec les nombres qui manquent dans la suite de 1 à 25.

                                                                                                                            Solutions 81 à 90

81. Citrons de Carole

Carole a numéroté huit citrons avec les chiffres de 1 à 8. Elle place les citrons 7 et 8 dans les positions indiquées. Elle veut placer les citrons 1 à 6 dans les autres cases pâles. La somme des numéros dans chaque rangée diagonale de trois cases doit être 12.

Complétez le tableau.

82. Grille de Carol

Carol a préparé une grille 6 × 6. Il y a inscrit 15 nombres de 1 à 6.

Complétez la grille avec des nombres de 1 à 6 de façon que chaque nombre apparaisse une seule fois dans chaque ligne et dans chaque colonne.

83. Mouche de Félix

Félix place une mouche dans la grille ci-après. La mouche fait d’abord un saut en L comme le cavalier aux échecs. Dans le saut suivant, elle atteint une case voisine horizontalement ou verticalement. Par la suite, les sauts se font en alternance : en L, puis horizontalement ou verticalement. Les cinq premiers sauts sont donnés.

Complétez le chemin de la mouche pour qu’elle atteigne toutes les cases une et une seule fois, sans passer par les deux cases noires.

84. Leçons d’Irma

Après avoir terminé d’apprendre ses leçons, Irma a tracé une grille 3 × 3. Elle veut y placer les nombres de 1 à 9. La somme des nombres de chaque ligne est indiquée à droite et celle de chaque colonne en bas. Le 9 est en bonne position.

Disposez les nombres de 2 à 8 dans cette grille.

85. Boules de Cédric

Dans un sac, Cédric a placé cinq boules numérotées de 1 à 5. Il pige en même temps trois boules et il fait la somme des numéros.

Combien y a-t-il de combinaisons possibles ?

86. Noisettes de Zacharie

Zacharie a fait neuf petits sacs de noisettes comportant de 3 à 11 noisettes. Il veut placer ses sacs dans une grille 3 × 3. Il a déjà déposé deux sacs aux bons endroits : un sac de 10 noisettes et un autre de 11 noisettes.

Disposez les autres sacs pour qu’il y ait 21 noisettes dans chaque rangée horizontale, verticale et diagonale.

87. Cadeau du parrain

Clara a reçu 55 pistoles de son parrain. Elle fait des groupes de 1 à 10 pistoles. Elle veut placer les pièces dans la grille ci-après. Il doit y avoir 18 pistoles dans chaque rangée de trois ou de quatre cases accolées horizontalement et verticalement. Clara commence par placer les groupes de 5 et de 10 pistoles.

Distribuez les autres groupes de pistoles.

88. Alice la rapide

Liane a laborieusement formé un carré latin avec les lettres de son prénom. Chaque lettre apparaît une seule fois dans chaque ligne et dans chaque colonne. Elle montre son carré à Alice.

Alice réussit alors un carré latin avec les lettres de son prénom en quelques secondes. Comment a-t-elle procédé ?

89. Fou de Josée

Josée prend un fou et le pose dans la case 1 de la grille ci-après. Celui-ci se déplace en diagonale, mais d’un seul pas à la fois. Quand il est incapable de bouger, il peut avancer horizontalement ou verticalement d’un seul pas. Josée a numéroté les quatre premiers sauts.

Continuez à déplacer le fou pour qu'il atteigne toutes les cases une et une seule fois.

90. Lettres de Ruth

Ruth a écrit 10 lettres dans la grille ci-après. Elle désire placer une lettre différente dans chaque rangée horizontale et verticale en utilisant les lettres de B à F.

Complétez la grille.

                                                                                                                              Solutions 91 à 100

91. Croix de Lucas

Lucas a tracé la figure ci-après. Il y a écrit un 4. Il veut compléter la grille avec les nombres de 5 à 10. La somme doit être 21 dans chaque branche de la croix, dans chaque diagonale et même dans les trois cases blanches de la dernière rangée horizontale.

Distribuez les nombres.

92. Double A

Aaron dessine un double A avec des cercles et prépare des jetons. Il place les jetons 7, 9 et 13 aux endroits indiqués. Il lui reste alors six jetons de numéros différents de 2 à 7.

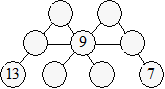
Placez ces six jetons pour la somme soit 18 dans chaque rangée de trois cercles reliés par une droite.

93. Pommes d’Arielle

Arielle achète 16 pommes : quatre marquées A, quatre marquées B, quatre marquées C et quatre marquées D. Elle place d’abord une pomme dans chaque coin. Les autres pommes doivent être disposées de manière qu’il y ait quatre marques différentes dans chaque rangée horizontale, verticale et diagonale.

Complétez la grille.

94. Taquin d’Yvan

Yvan place 15 jetons portant une lettre sur cette grille.

En déplaçant un jeton à la fois, il désire établir la phrase YVAN AIME TOUT CRU dont les lettres seront distribuées comme dans la grille suivante.

Glissez un jeton à la fois pour obtenir cette phrase.

95. Distribution de Méganie

Méganie a distribué 28 nombres dans la grille ci-après. Elle veut former des groupes de trois nombres dont la somme est 60. De plus, l’un des nombres est supérieur de 5 à un autre.

Combien y a-t-il de tels groupes dans cette grille ?

96. Retenue d’Antonia

Lors de sa retenue, Antonia prépare une grille 5 ´ 5. Elle y écrit 2 A, 2 B, 2 C, 2 D et 2 E.

Complétez la grille de façon que chaque rangée horizontale, verticale et diagonale contienne les cinq lettres différentes.

97. Rêve de Nicolas

Dans ses rêves récurrents, Nicolas a imaginé un tableau de nombres. Il place d’abord un 4 dans la case indiquée. Puis, dans les autres cases, il veut disposer chacun des nombres de 3 à 8. La somme dans chaque rangée verticale et diagonale doit être 16.

Complétez le tableau.

98. Jetons de Lucas

Lucas dessine une grille 3 × 3. Il y place trois jetons dans les cases ci-après. Il veut placer six autres jetons numérotés 5, 7, 9, 10, 12 et 14. La somme des numéros doit être 36 dans chacune des rangées horizontales, verticales et diagonales.

Complétez la grille.

99. Fou en délire

Antoinette s'amuse à déplacer un fou dans une grille. Ce dernier se déplace obliquement et avance d’un seul pas à la fois. Antoinette place d'abord le fou dans la case 1, puis dans la case 2. Elle a soin de numéroter les cases à mesure qu'elle le déplace.

Continuez à déplacer le fou pour qu'il atteigne la case colorée au neuvième pas.

100. Carré de Constant

Constant a préparé une grille dans laquelle on doit écrire des nombres de 1 à 5. Il a donné la somme des deux cases colorées de chaque ligne à droite et celle de chaque colonne en bas. Un 2 est déjà en place.

Complétez la grille avec des nombres de 1 à 5 de façon que chaque nombre apparaisse une seule fois dans chaque ligne et dans chaque colonne.

                                                                                                                           Solutions 101 à 110

101. Cellules de Pascal

Pascal veut inscrire les nombres de 1 à 9, sauf 8 dans la figure ci-après. La somme des nombres des quatre cases du coin inférieur gauche doit être 15. De plus, la somme doit être 13 dans chaque rangée horizontale et verticale de trois cases.

Disposez les nombres dans la grille.

102. Dés de Julie

Julie place cinq dés dans une boîte : deux marqués A et trois marqués B. Elle tire deux dés à la fois et les replace dans la boîte.

Combien y a-t-il de façons différentes d’obtenir deux dés ?

103. Monnaie de Ginette

Ginette dessine une grille 3 × 3 sur laquelle elle veut empiler des pièces de monnaie. Le nombre de pièces doit varier de 1 à 9. Ginette place d’abord 8 pièces dans une case et 6 dans une autre. De plus, elle indique le nombre de pièces qu’on doit trouver horizontalement et verticalement.

Complétez le tableau.

104. Jetons en bronze

Dans une boîte, il y a des jetons en bronze marqués par les nombres de 9 à 17. Lucie dispose d’abord trois jetons dans la grille ci-dessous.

Placez les autres jetons pour que la somme des nombres soit 39 dans chaque rangée horizontale, verticale et diagonale.

105. Mois de février

Naomie lance des balles sur une page de calendrier montrant le mois de février. Après chaque lancer, elle calcule la somme des chiffres des nombres atteints. Par exemple, pour 28, la somme des chiffres est 10.

Combien y a-t-il de possibilités qu’Isabelle atteigne une somme de 18 en lançant deux balles ?

106. Étoiles de Guillaume

Dans la grille ci-après, Guillaume a dessiné cinq étoiles.

Disposez trois autres étoiles pour qu’il y en ait deux dans chaque rangée horizontale et dans chaque rangée verticale.

107. Cartes d’Angéline

Angéline a dessiné des symboles du jeu de cartes dans la grille ci-après. Par la suite, elle veut remplir la grille, sauf les cases noires, avec ces symboles. Dans chaque ligne, dans chaque colonne et dans chacune des deux diagonales, il doit y avoir chacun des quatre symboles.

Complétez la grille.

108. Boules de Narcisse

Narcisse prend neuf boules numérotées de 1 à 9. Il remet la boule 3 dans son sac. Puis, il place la 2 à l’endroit indiqué dans la grille.

Disposez les autres boules pour que la somme des numéros soit 14 dans chaque rangée horizontale et verticale.

109. Cavalier de Jason

Jason prend un cavalier du jeu d’échecs et le promène sur une grille 4 × 5. Le cavalier passe d’une case à l’autre en faisant un L. Le cavalier de Jason a parcouru les huit premières cases suivantes.

Complétez le chemin du cavalier pour qu’il atteigne toutes les cases.

110. Coffre de Nathalie

Nathalie a placé le même nombre de billes dans chaque rangée horizontale, verticale et diagonale d'un coffre ayant neuf compartiments. Il y a 10 billes dans le compartiment A, 6 dans le B et 7 dans le C.

Combien y a-t-il de billes dans le coffre ?

                                                                                                                             Solutions 111 à 120

111. Tour de Catherine

Catherine a appris à déplacer une tour sur son jeu d’échecs. La tour de Catherine avance d’un seul pas à la fois horizontalement et verticalement, jamais en diagonale. La jeune fille trace une grille 5 × 5. Elle marque cinq cases d’un numéro qui représente le rang du pas dans le parcours.

Trouvez un chemin qui part de la case 1 et qui, en passant par les cases marquées, se termine à la case 25. Toute case doit être atteinte une et une seule fois.

112. De un à six

Michel a préparé une grille dans laquelle on doit écrire des nombres de 1 à 6. Il a donné la somme des deux dernières cases de chaque ligne à droite et celle des deux dernières cases de chaque colonne en bas. Quatre nombres sont déjà en bonne position.

Complétez la grille avec des nombres de 1 à 6 de façon que chaque nombre apparaisse une seule fois dans chaque ligne et dans chaque colonne.

113. Grille de Jean-Yves

Dans cette grille, Jean-Yves a écrit chacun des chiffres de 1 à 4 une seule fois.

Dans les cases sauf les noires, placez des chiffres de 1 à 4 pour que les chiffres soient différents dans chaque ligne, colonne et diagonale.

114. Pièges à ours

Maman ourse est placée à gauche et son petit ourson l’attend à droite. Des sentiers se présentent devant elle. Maman ourse ne doit jamais revenir en arrière. Toutefois, elle a peur des pièges qui pourraient y être dissimulés. Elle se dit : « S’il y a plus de huit chemins différents pour se rendre à mon ourson, je vais tomber dans un piège. Dans ce cas, je serais mieux de ne pas bouger. »

Quelle décision devra prendre maman ourse ?

115. Dominos d’Alyssa

Alyssa a décidé de fabriquer un jeu de dominos. Elle marque chaque pièce de points noirs dont le nombre représente les combinaisons possibles des entiers de 1 à 6 pris deux à deux. Par exemple, le plus petit domino est (1, 1) et le plus grand (6, 6).

Combien de pièces Alyssa devra-t-elle fabriquer ?

116. Carré de Louise

Louise veut inscrire dans la grille carrée ci-après les nombres impairs de 1 à 13. La somme doit être 27 dans chaque rangée horizontale, verticale et diagonale. Deux nombres sont déjà posés.

Complétez la grille.

117. Diagonales d’Albert

Dans le tableau ci-après, Albert a placé le 9 et le 10. Il veut disposer les nombres de 3 à 8 dans les cases pâles. La somme dans chaque rangée diagonale de trois cases doit être 20.

Complétez le tableau.

118. Deux sœurs

Rose s’amuse à grouper deux par deux les lettres de son prénom en conservant l’ordre des lettres. Elle a trouvé les six groupes : (R, O), (R, S), (R, E), (O, S), (O, E) et (S, E). Sa sœur Laurie veut faire de même avec son prénom.

Combien Laurie devra-t-elle former de groupes de deux lettres ?

119. Coquilles de Justine

Justine prépare neuf coquilles et les numérote de 1 à 9.

s Les quatre cellules grises du triangle doivent recevoir les coquilles de numéros pairs.

s La somme des extrémités de la base doit être 11.

s La somme des numéros de chaque rangée de quatre cellules doit être 19.

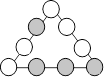
Placez les neuf coquilles sur les côtés du triangle.

120. Grille de Carmen

Carmen a préparé une grille 6 × 6. Elle y a inscrit 16 lettres choisies parmi les lettres de son prénom.

Complétez la grille avec des lettres de CARMEN pour que chaque lettre apparaisse une seule fois dans chaque ligne et dans chaque colonne. 

     
       Lire la suite