Solutions 121 à 130

121. Figure de Coralie

Coralie a écrit 7, 8 et 9 dans cette figure. Elle désire placer les nombres de 1 à 5 pris chacun une fois de façon que la somme soit 15 dans chaque rangée de trois cases.

Distribuez les nombres.

122. Trios de Lucette

Lucette a préparé le tableau de nombres ci-après. Parmi ceux-ci, il y a des groupes de trois nombres différents dont la somme est 32. La différence est alors 4 entre les deux plus petits nombres.

Combien y a-t-il de tels trios ?

123. Tableau d’Ariane

Dans le tableau ci-après, Ariane veut placer les nombres de 3 à 10 dans les cases. La somme dans chaque rangée diagonale de trois cases doit être 20. Ariane a déjà placé 5 et 7.

Complétez le tableau.

124. Cercles en double

Julie a tracé la grille ci-après qui contient des cases noires et des cercles.

Combien peut-on compter de carrés 3 × 3 qui contiennent exactement deux cercles ?

125. Grille de Liane

Dans la grille ci-après, Liane désire placer les nombres de 1 à 10, sauf 3 et 7. La somme doit être 15 dans chaque rangée horizontale, verticale et diagonale de deux et de trois cases. Le 6 et le 9 sont en bonne position.

Complétez la grille.

126. Mia en géographie

À chaque mois de l’année scolaire, Mia doit passer une épreuve de connaissances en géographie sur 10 points. Au début de l’année, elle a écrit la première lettre des sept premiers mois dans la figure ci-après. À chaque mois, elle écrit sa note qui est entière. À la fin, elle se rend compte que la somme de ses notes est 22 dans chaque rangée de trois mois.

En octobre, elle a eu trois points de moins qu’en septembre.

En novembre, elle a eu trois points de moins qu’en décembre.

En novembre, elle a eu la même note qu’en janvier.

En février, elle a eu la même note qu’en mars.

Complétez le tableau en inscrivant les notes de Mia pour chaque mois.

127. Jetons de Carl

Carl dessine une grille 3 × 3. Il découpe huit jetons sur lesquels il écrit les lettres qui apparaissent dans la grille de droite ; puis, il dépose chaque jeton dans cette grille comme il est indiqué.

Déplacez les jetons un à un sur toute case libre en les glissant horizontalement ou verticalement. À la fin, vous devez obtenir la disposition de la grille de gauche.

128. Triangles de Dariane

Dariane a préparé la figure ci-après. Elle veut y placer chacun des nombres de 1 à 9. La somme des trois nombres sur les sommets d’un triangle doit être égale à 15. Le 1 et le 2 sont en bonne position.

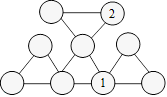
Distribuez les autres nombres.

129. Surprise de Michel

Dans la grille ci-après, Michel choisit cinq nombres. Il prend successivement un seul nombre par ligne et un seul nombre par colonne. Il additionne ces cinq nombres.

Combien y a-t-il de sommes possibles ?

130. Rectangle de Claire

Claire a écrit les nombres de 1 à 5 sur la première ligne de la grille ci-après. Elle doit placer les nombres de 6 à 10 sur la deuxième ligne et les nombres de 11 à 15 sur la troisième ligne. La somme dans chaque colonne doit être 24.

Complétez la grille.

                                                                                                                          Solutions 131 à 140

131. Poules d’Emmanuel

Emmanuel prend huit œufs et les numérote de 2 à 10, sauf 6. Il dessine une figure formée de huit alvéoles comme ci-après où il a l’intention de déposer ses œufs. Il a déjà placé les œufs numéros 7 et 10.

Placez les autres œufs de façon que la somme de leur numéro soit 18 par rangée de trois alvéoles.

132. Suites de Rébecca

Rébecca a écrit les nombres de 1 à 9 dans la grille. Elle forme des nombres en regroupant les chiffres adjacents en tout sens. Un chiffre ne peut servir qu’une fois dans un nombre. Par exemple, on pourrait lire 2574.

Combien peut-on compter de nombres de trois chiffres qui commencent par 9 ?

133. Cases de Noémie

Dans la figure ci-après, Noémie veut placer chacun des nombres de 1 à 11, sauf 6 et 8. La somme des nombres de chaque rangée de deux ou de trois cases accolées doit être égale à 14. Le 1 et le 7 sont en bonne position.

Complétez la figure.

134. Dards de Mona

Mona place au mur le tableau ci-après. Elle doit lancer trois dards sur le tableau de telle manière que la somme des numéros atteints est 28.

Combien y a-t-il de possibilités d’atteindre trois cases qui permettent une somme de 28 ?

135. Tableau de Martine

Martine a dessiné la figure ci-après qui contient sept cases colorées. Dans une case, elle a écrit 10. Elle veut écrire les nombres 2, 3, 4, 5, 7 et 8 de façon que la somme des nombres dans chacune des deux rangées horizontales de trois cases et des deux diagonales soit 17.

Disposez les nombres.

136. Blancs de Cassandre

Cassandre a composé un carré magique 5 × 5 en y disposant les nombres de 1 à 25. La somme des nombres était de 65 dans chaque rangée horizontale, verticale et diagonale. Cassandre a effacé les nombres de 15 à 25.

Reconstituez le carré magique.

137. Barricade de Nick

Nick a inscrit 8 et 12 dans la figure ci-après. Il veut y disposer 2, 3, 4, 6, 7, 9 et 14. La somme doit être 20 dans chaque rangée de deux, de trois ou de quatre cases accolées autant horizontalement que verticalement.

Complétez la figure.

138. Différences de Marcelle

Marcelle a écrit neuf nombres dans la grille ci-après. Elle veut y placer des nombres de 1 à 5 de façon à ce qu’il n’y ait jamais deux nombres identiques horizontalement, verticalement et dans les deux diagonales.

Complétez la grille.

139. Philippe magique

Philippe a écrit les nombres de 1 à 6 sur la première ligne de la grille ci-après. Il doit placer les nombres de 7 à 13, sauf 10, sur la deuxième ligne et les nombres de 14 à 19 sur la troisième ligne. La somme dans chaque colonne doit être 30.

Complétez la grille.

140. Poussins en triangle

Raymonde a une collection de 26 poussins en peluche. Elle place 1, 2 et 4 poussins dans les coins du triangle comme il est indiqué. Elle veut placer d’autres poussins de façon qu’il y en ait le même nombre sur chaque côté du triangle.

Combien Raymonde doit-elle placer de poussins dans chacune des autres cases ?

                                                                                                                         Solutions 141 à 150

141. Groupes de Mathieu

Mathieu a trouvé le carré magique ci-après dans un livre. On y retrouve quatre lignes, quatre colonnes et deux diagonales dont la somme est 34. Il existe toutefois d’autres groupes de quatre nombres dont la somme est 34.

 Combien y a-t-il de carrés 2 × 2 dont la somme est 34 ?

142. Laurine calcule

Laurine a écrit 8, 9 et 10 dans la grille ci-après. Elle veut y placer les nombres de 1 à 7. La somme doit être 16 dans chaque rangée horizontale et verticale de trois cases. Sur la dernière ligne, on considère seulement les trois premières cases.

Complétez la grille.

143. Sœur de Magalie

Magalie veut placer chacun des nombres de 1 à 12 : six nombres dans les petits carrés, six dans les triangles intérieurs. Le nombre de chaque petit carré est la somme des nombres de deux triangles adjacents. Sa sœur a déjà placé 1, 10, 11 et 12.

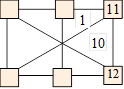
Placez les nombres de 2 à 9.

144. Sommes de Zénon

Zénon a préparé une grille dans laquelle on doit écrire des nombres de 1 à 5. Il a donné à droite la somme des deux dernières cases de chaque ligne et en bas celle des deux dernières cases de chaque colonne.

Complétez la grille avec des nombres de 1 à 5 de façon que chaque nombre apparaisse une seule fois sur chaque ligne et dans chaque colonne.

145. Piles d’Émile

Émile a préparé trois piles de jetons numérotés comme ci-après.

Combien y a-t-il de façons d’avoir 80 points en prenant autant de jetons qu’on veut ?

146. Cellules de Beauvais

Beauvais a posé les jetons 9, 10 et 12 dans la figure ci-après. Il veut maintenant y placer  chacun des jetons numérotés de 1 à 7, sauf 3. La somme des numéros de trois jetons doit être 20 sur chaque côté de la figure et dans la diagonale marquée A.

Trouvez une disposition.

147. Au ping-pong

Jessica lance des boules de ping-pong sur la grille carrée ci-après. À chaque lancer de trois boules, elle vise à obtenir une somme de 30.

Combien de groupes Jessica pourra-t-elle atteindre ?

148. Maélie calcule

Dans le tableau ci-après, Maélie a placé un 3, un 5 et un 9. Elle doit placer les nombres de 2 à 9, sauf 4, dans les cases vides. La somme dans chaque rangée verticale et diagonale de trois cases accolées doit être 17.

Complétez le tableau.

149. Jérémie combine

Au début de l’année scolaire, la mère de Jérémie lui a acheté trois t-shirts, trois paires de jeans et trois paires d’espadrilles. Jérémie choisit chaque jour un ensemble tel qu’un article est porté une seule fois avec chacun des deux autres.

Pendant combien de jours Jérémie pourra-t-il porter un ensemble différent ?

150. Clés de Laurie

Laurie a dessiné la figure ci-après composée de sept coffrets. Elle veut placer ses 28 clés USB dans les coffrets, tout en ayant un nombre différent par coffret. Les coffrets marqués A ensemble doivent contenir sept clés, les B huit clés.

Placez les clés USB de façon qu’il y en ait 11 dans chaque rangée de trois coffrets accolés.

                                                                                                                             Solutions 151 à 160

151. Dominos de Mathias

Mathias prépare huit dominos : (1, 2), (1, 3), (1, 4), (1, 6), (2, 5), (3, 3), (3, 4), (3, 5). Il place trois dominos sur le contour du tableau.

Placez les cinq autres dominos de façon qu’il y ait 15 points sur chaque côté du tableau.

152. Erreurs de Victoria

Victoria a préparé la grille ci-après dans laquelle la somme des nombres devrait être 27 sur chaque ligne.

Intervertissez deux couples de nombres de façon que la somme soit 27 dans chaque ligne.

153. Poisson d’avril

C’est le 1^er avril. Nicolas dessine un poisson comme ci-après. La figure contient trois triangles. Nicolas veut placer les nombres 2, 2, 4, 5, 6 et 7 dans les cases de façon que la somme des trois sommets de chacun des trois triangles soit 13.

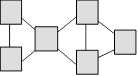
Distribuez les nombres dans la figure.

154. Cellules de Simon

Simon a dessiné un carré sur les côtés duquel il a dessiné huit cellules. Il y a inscrit 11 et 13. Il veut placer 2, 4, 5, 6, 7, 9 de façon que la somme soit 20 sur chaque côté du carré.

Complétez le carré.

155. Tirelire de Gaétan

Gaétan vide sa tirelire qui contient moins de 20 pièces.

Il y trouve des pièces de 10 sous et de 25 sous.

Combien y a-t-il de façons de faire trois dollars avec au moins une pièce de 10 sous et une pièce de 25 sous ?

156. Cellules d’Irma

Irma a inscrit 10 dans la figure ci-après. Elle veut placer 1, 2, 3, 4, 5, 11 et 12 dans les cellules de façon que la somme de chaque rangée de deux ou de trois cellules accolées soit 16.

Complétez la figure.

157. Jetons de Lorraine

Lorraine a préparé neuf jetons et les a numérotés de 1 à 9. Elle veut distribuer les jetons de façon que les numéros de chaque trio aient une somme de 15. Les jetons 5, 7 et 3 sont en bonne position.

Trouvez une façon de distribuer les autres jetons.

158. Lettres de Renaud

Renaud a écrit des lettres A, B et C dans la grille 3 × 3 ci-après. Chaque lettre représente un chiffre différent. La somme des nombres est donnée en regard de chaque ligne et de deux colonnes.

Quelle est la somme des nombres de la première colonne ?

159. Secret de nombres

Carole inscrit 13 et 15 dans la grille ci-après. Elle veut placer d’autres nombres inférieurs à 15 dans les cases vides. La somme des nombres de chaque rangée horizontale, verticale et diagonale doit être 27.

Complétez la grille.

160. Jetons d’Anna

Anna découpe des jetons et les numérote 2, 3 et 20. Elle a plusieurs jetons numérotés 2 et 3. Toutefois, elle a un seul 20 qu’elle doit prendre.

Combien y a-t-il de façons d’avoir 45 points avec les jetons d’Anna ?

                                                                                                                          Solutions 161 à 170

161. Cellules de Majorie

Majorie a écrit 7 et 10 dans la figure ci-après. Elle doit y disposer sept autres nombres : 1, 2, 3, 4, 5, 6, 9 dans les cellules. La somme doit être 15 sur chaque côté du carré et dans les deux cellules accolées de la deuxième ligne. 

Distribuez les sept nombres.

162. Roue de Léonard

Dans cette roue, Léonard veut placer chacun des nombres de 3 à 11. La somme doit être 21 dans chaque rangée de trois cercles reliés par une droite.

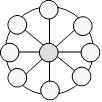
Quel devra être le nombre du milieu ?

163. Chocolats de Lucie

Lucie dispose 1, 2 et 3 chocolats dans les cases de la figure ci-après. Elle veut placer des chocolats dans les trois autres cases de façon qu’il y ait le même nombre de chocolats sur chaque côté du triangle. Aucune case ne doit avoir le même nombre de chocolats.

Au minimum, de combien de chocolats a-t-elle besoin pour compléter le triangle ?

164. Lettres d’Hugues

Hugues a préparé la grille ci-après dans laquelle chaque lettre représente un chiffre différent. La somme des nombres est 66 dans chaque rangée horizontale, verticale et diagonale. La valeur de F est 8 et celle de H est 2.

Reconstituez la grille.

165. Hugo calcule

Dans le tableau ci-après, Hugo veut placer les nombres de 1 à 8 dans les cases. La somme dans chaque rangée diagonale de trois cases doit être 14. Hugo a déjà placé 7 et 8.

Complétez le tableau.

166. Pairs de Laurie

Dans la grille ci-après, Laurie veut placer chacun des nombres de 1 à 9. Pour quatre rangées, la somme est donnée à droite et en bas. Seules les cases de la première ligne et celle du centre doivent recevoir des nombres pairs. Le 6 est en bonne position.

Complétez la grille.

167. Sieste de lapins

Marthe a cinq petits lapins. Elle attribue à chacun un numéro différent qui est un diviseur de 48. La somme de ces numéros doit être 48. Elle place cinq tapis comme ci-dessous.

Disposez chacun des lapins sur un tapis de façon que le produit des numéros soit le même dans chacune des deux rangées de trois lapins.

168. Figure de Méliane

Méliane a dessiné la figure ci-après dans laquelle elle a écrit 8, 9 et 11. Il faut placer les nombres de 1 à 7, sauf 3. La somme des nombres de 2, 3, et 4 cases accolées horizontalement et verticalement doit être égale à 16.

Compétez la grille.

169. Mois de janvier

Isabelle lance des balles sur un calendrier montrant le mois de janvier. Après chaque lancer, elle calcule la somme des chiffres des nombres atteints. Par exemple, si les balles touchent 12 et 19, la somme des chiffres est 1 + 2 + 1 + 9 = 13.

Combien y a-t-il de possibilités qu’Isabelle atteigne une somme de 12 en lançant deux balles et en atteignant seulement les cases de la deuxième et de la troisième ligne ?

170. Cavalier d’Étienne

Étienne pose le cavalier sur 72. Il le déplace en L comme aux échecs en faisant une opération de multiplication ou de division avec le nombre de chaque saut et en passant par toutes les cases. Le résultat final est également 72.

Dans quel ordre, le cavalier d’Étienne a-t-il visité les cases ?

                                                                                                                         Solutions 171 à 180

171. Figure de Clermont

Clermont a inscrit 1, 5 et 7 dans la figure ci-après. Il veut placer les nombres 2, 5, 6, 8, 9 et 11 de façon que la somme soit la même dans chaque rangée horizontale et verticale.

Complétez la figure.

172. Cellules d’Arnaud

Arnaud a disposé neuf cellules sur les côtés d’un triangle. Il veut placer les nombres de 1 à 9 pris chacun une seule fois dans les cellules. La somme des nombres sur chaque côté doit être égale à 23. Trois nombres sont en bonne position.

Distribuez les nombres de 4 à 9.

173. Sommets de Louise

Dans les cases de la figure ci-après, Louise veut écrire chacun des nombres de 1 à 6. Elle fait la somme des nombres qui sont aux sommets des triangles. Les sommes sont A, B et C.

Quelle est la plus grande valeur de A + B + C ?

174. Cartes de Chloé

Chloé prend les six cartes illustrées ci-après. Elle agence les cartes deux par deux : une de carreau et une autre de trèfle.

Combien y a-t-il de façons de combiner les cartes de façon que la somme des numéros soit inférieure à 11 ?

175. M de Maria

Maria a dessiné la figure ci-après. Elle veut y placer chacun des nombres de 1 à 8 une fois, sauf 2. La somme des nombres doit être 16 dans les deux colonnes de trois cases et dans les deux diagonales de trois cases. Un 3 et un 9 sont en bonne position.

Complétez la figure.

176. Sommeil d’Alicia

Avant de se coucher, Alicia trace une grille 3 × 3. Elle veut écrire des nombres dans la grille de façon que la somme soit 36 dans chaque rangée horizontale, verticale et diagonale.

• Les nombres 5, 14 et 17 doivent apparaître sur la première ligne.

• Les nombres 7, 14, 15 doivent apparaître dans la troisième colonne.

• Les nombres 7, 12 et 17 doivent apparaître dans la diagonale marquée A.

Remplissez la grille.

177. Carré de Jules

Jules a écrit des nombres dans la grille carrée ci-après. Dans chaque rangée horizontale, les nombres sont les bons, mais pas nécessairement dans les bonnes cases.

Placez les nombres aux bons endroits pour que la somme soit identique dans chaque rangée horizontale, verticale et diagonale.

178. Un H élargi

Augustin a préparé la figure ci-après. Il y a inscrit 1 et 9. Il veut placer chacun des nombres de 1 à 8, sauf 2 et 3. La somme doit être 16 dans chaque rangée horizontale et verticale de trois ou de quatre cases.

  Complétez la figure.

179. Timbres de Mario

Mario prend neuf sachets de timbres. Sur chaque sachet, il indique le nombre différent de timbres, qui varie de 3 à 11. Il trace un carré 3 × 3. Dans chaque case, il doit placer un sachet. Les sachets de 9 et de 10 timbres sont à la bonne place. La somme des timbres par rangée est indiquée à droite et en bas.

Placez les autres sachets de timbres.

180. Un coup de vent

Ghislaine a disposé des jetons numérotés de 1 à 25 dans cette grille. Un coup de vent a emporté tous les jetons dont le numéro est pair.

Complétez la grille de telle manière que la somme est la même dans chaque rangée horizontale, verticale et diagonale.

        Lire la suite