Solutions 181 à 190

181. Médaillons de Noémie

Flavie prend sept médaillons et les numérote 6, 7, 8, 9, 10, 11 et 12. Elle doit placer les médaillons dans les cases de la figure ci-après de façon que la somme soit 27 dans chaque rangée horizontale, verticale et diagonale de trois cases accolées. Le médaillon 12 est en bonne position.

Distribuez les autres médaillons.

182. Renversés de Claudin

Claudin veut placer 16 nombres inférieurs à 40 dans la grille ci-après. Les cases marquées de la même lettre doivent recevoir deux nombres dont l’un est le renversé de l’autre. Six nombres sont en bonne position.

Placez des nombres de façon que la somme soit 68 dans chaque rangée horizontale, verticale et diagonale.

183. Jetons de Cléo

Cléo prend neuf jetons et les numérote de 1 à 9. Il place le jeton 1 dans le coin supérieur gauche de la figure ci-après. Il désire disposer les autres jetons de telle manière que deux nombres consécutifs en ordre numérique ne soient jamais voisins horizontalement et verticalement.

Trouvez une façon de distribuer les huit autres jetons.

184. Dé de Maryse

Maryse s'est fabriqué un dé. Elle a inscrit sur ses faces ces six nombres.

1       2       4       5       6       8

Elle lance trois fois le dé et additionne les nombres obtenus. Par exemple, au premier lancer, elle a obtenu 4, au deuxième 1 et au troisième 6. Alors, la somme des résultats est 11.

Combien peut-on compter de combinaisons formées de nombres différents avec trois lancers lorsque la somme est 15 ?

185. Magie d’Éva

Éva désire placer chacun des nombres de 1 à 10 dans cette grille de façon que la somme soit 22 dans chacune des quatre rangées de trois ou de quatre cellules.

s La somme des nombres des deux cellules A est 10.

s La somme des nombres des deux cellules B est 9.

s La somme des nombres des deux cellules C est 8.

Placez les nombres de 1 à 10 dans cette grille.

186. Numéros d’Hélène

Hélène dispose les jetons dont les numéros sont 2, 4 et 10 dans la grille ci-après. Elle veut placer les jetons 2, 3, 4, 5, 7, 8, 11 et 14. La somme doit être 19

• dans les deux groupes de deux cases de la première ligne

• dans les quatre cases de la dernière ligne

• dans les trois colonnes de trois cases.

Trouvez une disposition des jetons.

187. Cellules de Lukas

Lukas a préparé la figure ci-après et y a inscrit les nombres 7 et 8. Il désire disposer chacun des nombres de 1 à 6 de façon que la somme soit 14 dans chacune des quatre rangées diagonales.

Complétez la figure.

188. Tout en magie

Didier a construit un carré magique d'ordre 5 avec les nombres de 1 à 25. Il a effacé les nombres de 1 à 14.

Complétez ce carré de façon que la somme des nombres de chaque rangée de cinq éléments soit 65 horizontalement, verticalement et en diagonale.

189. Sac de noix

Louis-Félix a un sac de noix. Sa mère lui dit :

« Tu vois cette figure. J’y ai déjà placé 11 noix dans une case. Il te faut placer 3, 4, 5, 6, 7, 8, 9 et 10 noix dans les cases vides. Il doit y avoir 21 noix dans chaque rangée horizontale, verticale et diagonale de trois cases.

Répartissez les noix.

190. Tableau de Jeanne

Jeanne a préparé le tableau ci-après. Chaque lettre représente un chiffre différent. Les nombres sont additionnés horizontalement et verticalement.

Reconstituez le tableau en chiffres.

                                                                                                                         Solutions 191 à 200

191. Différences de Bernard

Bernard écrit le nombre 54 321 sur la première ligne de la grille ci-après.

s Sur la deuxième ligne, il écrit le plus grand nombre pair formé des cinq mêmes chiffres. Dans chaque colonne, le chiffre choisi doit être différent du chiffre du premier nombre.

s Sur la troisième ligne, il écrit le plus grand nombre pair formé des cinq mêmes chiffres. Dans chaque colonne, le chiffre choisi doit être différent du chiffre du premier et du deuxième nombre.

Complétez le tableau.

192. Roch à la cuisine

Avant de laver la vaisselle, Roch aime bien s’amuser un peu. Il numérote six cartes : 2, 4, 5, 6, 9, 10 et dessine l’égalité suivante comportant des fractions.

Disposez les six cartes de façon à ce que l’égalité soit vraie.

193. Thomas le clochard

Après avoir contemplé le ciel, Thomas a tracé la figure ci-après dans laquelle il a dessiné cinq étoiles (É) et quatre cloches (C). Il désire placer chaque nombre de 1 à 5 sur les étoiles et chaque nombre de 6 à 9 sur les cloches. La somme doit être 12 dans les rangées de trois cases suivantes :

• la première rangée horizontale

• la troisième rangée horizontale

• les deux rangées verticales

• les deux diagonales.

Disposez les nombres de 1 à 9 dans cette figure.

194. Un coin vide

Fanny a écrit 9, 14 et 13 dans trois coins de la grille ci-après. Elle doit remplir ce carré de façon que la somme soit 33 dans chaque rangée horizontale, verticale et diagonale.

Quel est le nombre qui devrait apparaître dans le coin vide ?

195. Couples de Vincent

Vincent a écrit deux lettres dans chaque case de la grille ci-après. Chaque lettre représente un chiffre différent. Deux lettres accolées forment un nombre de deux chiffres. La somme des nombres de chaque ligne, de chaque colonne et de chaque diagonale est 72.

Reconstituez la grille.

196. Cases de Karo

Karo veut placer les nombres de 3 à 10 dans les cases du tableau ci-après. La somme dans chaque rangée diagonale de trois cases doit être 20. Karo a déjà placé le 7 et le 8.

Complétez le tableau.

197. Magie de Léa

Léa a écrit les nombres de 1 à 25 dans la grille ci-après. Elle a effacé 13 nombres. La somme des nombres de chaque ligne, chaque colonne et chaque diagonale doit être 65.

Complétez la grille avec les nombres qui manquent dans la suite de 1 à 25.

198. Coccinelles domestiques

Victoria a dressé cinq coccinelles : A, B, C, D et E. Elle leur a préparé chacune une stalle comme ci-après. La coccinelle B doit toujours occuper la même stalle, soit la deuxième à partir de la gauche. De plus, les coccinelles D et E doivent toujours être voisines.

Combien y a-t-il de façons différentes de placer les coccinelles ?

199. Quinte de toux

Entre deux quintes de toux qui interviennent à toutes les cinq minutes, Pierrette observe une grille 5 × 5 dans laquelle neuf nombres sont inscrits. Elle doit compléter la grille avec des nombres de 1 à 5 de telle manière que la somme est 15 dans chaque rangée horizontale, verticale et diagonale. Chaque rangée doit être constituée de nombres différents, sauf pour une diagonale.

Complétez la grille.

200. Biscuits de Délima

Délima numérote sept biscuits de 1 à 7. Elle veut placer les biscuits dans le tableau ci-après. La somme doit être 11 dans chaque rangée de deux ou de trois cases accolées horizontalement et verticalement.

Disposez les biscuits.

                                                                                                                      Solutions 201 à 210

201. Balcon fleuri

Au centre du balcon de Gilberte se trouve un poteau. Pour égayer les lieux, Gilberte a posé huit boîtes de fleurs autour du poteau, soit trois de chaque côté. Le nombre de fleurs par boîte varie de 4 à 11, aucune boîte n’ayant le même nombre. On sait que la boîte du coin supérieur gauche contient quatre fleurs.

Complétez les sept autres boîtes de façon qu’il y ait 23 fleurs sur chaque côté.

202. Jumeau de Luce

Luce a écrit les lettres de son prénom dans la grille ci-après. Chaque lettre représente un nombre différent. La somme de deux lignes est donnée à droite et celle de deux colonnes en bas.

Quelle est la somme des lettres de LUC ?

203. Coins de Camille

Dans la grille 3 × 3 ci-après, Camille écrit les nombres de 1 à 9. La somme des nombres dans chaque rangée horizontale, verticale et diagonale est 15. La somme des nombres des quatre coins est 20.

Camille dit à son amie : « Place les nombres pairs de 2 à 18 dans la grille pour avoir une somme de 30 dans chaque rangée. »

Quelle sera alors la somme des nombres des quatre coins ?

204. Magie de Léo

Léo a composé un carré magique avec chacun des nombres de 1 à 25. Il a effacé les nombres supérieurs à 11.

Complétez la grille de façon que la somme des nombres soit égale à 65 horizontalement, verticalement et diagonalement.

205. Moutons de Thomas

Thomas surveille 81 moutons dans neuf enclos disposés en un carré comme ci-après. Il y a le même nombre de moutons dans chaque rangée horizontale, verticale et diagonale. Dans trois enclos, le nombre de moutons est indiqué.

Combien y a-t-il de moutons dans l’enclos du coin inférieur gauche ?

206. Triangle d’Olivia

Olivia a disposé neuf cellules sur les côtés d’un triangle. Elle veut placer dans les cellules les nombres de 1 à 9 pris chacun une seule fois. La somme des nombres sur chaque côté doit être égale à 20. Trois nombres sont en bonne position.

Distribuez les autres nombres.

207. Gilets personnalisés

Sur chacun de ses gilets, Louise colle un nombre formé des chiffres 2, 3, 4 et 5, chacun une seule fois.

Combien de gilets peuvent être ainsi numérotés ?

208. Grille de Firmin

Lyne donne neuf nombres à Firmin : 7, 8, 9, 12, 13, 14, 17, 18 et 19. Elle lui dit :

« Dispose ces nombres dans la grille ci-après de façon que la somme des nombres dans chaque rangée horizontale, verticale et diagonale soit la même. Deux nombres sont à la bonne place. »

Complétez la grille.

209. Monnaie de Zoé

Depuis plusieurs mois, Zoé conserve des pièces de monnaie dans sa tirelire.

Un jour, elle décide de retirer des pièces de 5 sous et de 10 sous.

Elle assemble alors des pièces pour totaliser 50 sous.

Chaque assemblage est différent.

Quel montant total Zoé aura-t-elle quand elle aura terminé sa tâche ?

210. Diagonales de Line

Dans le tableau ci-après, Line veut placer les nombres de 1 à 8 dans les cases. La somme dans chaque rangée diagonale de trois cases doit être 13. Le 8 est déjà placé.

Complétez le tableau.

                                                                                                                           Solutions 211 à 220

211. Carré de Léonard

Léonard a composé un carré magique dans lequel la somme des nombres dans chaque rangée horizontale, verticale et diagonale est 40. Il a effacé huit nombres.

Trouvez une façon de compléter le carré avec des nombres que vous choisissez.

212. Une belette affamée

Assise au point A, une belette se dore au soleil. Elle voit un mulot au point B. Elle se dit : « S’il y a plus de huit chemins pour aller au point B, je vais attraper ce mulot. Sinon, j’ai bien peur que le mulot va déguerpir. » La belette se déplace de gauche à droite et de haut en bas, jamais en diagonale, en passant par les points.

La belette va-t-elle pouvoir se régaler du mulot ?

213. Grille de Carl

Carl a donné une valeur numérique à chaque lettre de son prénom. Il a écrit les lettres dans la grille. Il a donné la somme des valeurs dans deux lignes et deux colonnes.

Quelle est la somme des valeurs de la troisième ligne ?

214. Tableau de Lina

Dans le tableau ci-après, Lina veut placer les nombres de 1 à 13, sauf 7. La somme doit être 28 dans chaque rangée horizontale et 21 dans chaque rangé verticale. Lina a déjà placé 12 et 13.

Complétez le tableau.

215. Double d’Alain

Alain a tracé un double A. Il y a inscrit 7, 9 et 11. Par la suite, il veut écrire chacun des nombres de 2 à 8, sauf 3. La somme doit être 19 dans la deuxième rangée horizontale et dans chacune des quatre diagonales de trois cases.

Distribuez ces nombres dans la figure.

216. Somme de Laurette

Laurette a dessiné une grille 3 × 3. Elle veut y placer chacun des nombres de 5 à 11. La somme doit être 27 dans chaque rangée horizontale, verticale et diagonale de trois cases. Le 12 est en bonne position.

Distribuez les nombres.

217. Cadeau de Quintilius

Quintilius a préparé une grille dans laquelle il veut écrire des nombres de 1 à 5. Il a donné la somme des nombres des deux dernières cases de chaque ligne à droite et de chaque colonne en bas. Comme cadeau, il a indiqué la position d’un 1.

Complétez la grille avec des nombres de 1 à 5 de façon que chaque nombre apparaisse une seule fois dans chaque rangée horizontale et verticale.

218. Somme de Sophia

Sophia a dessiné la figure ci-après. Elle veut y placer chacun des nombres de 3 à 11, sauf 9. La somme des nombres doit être 18 dans chaque rangée horizontale et verticale de deux ou de trois cases. Le 11 est en bonne position.

Distribuez les nombres.

219. Cellules de Jasmin

Dans les cellules de la figure ci-après, Jasmin désire disposer chaque nombre de 1 à 9 une seule fois. La somme doit être 25 dans chacune des deux diagonales et 30 dans les quatre coins. Le 6 et le 9 sont en bonne position.

Trouvez une façon de distribuer les nombres.

220. Bonbons de Rosalie

Rosalie est une vraie bonbonnière. Après avoir reçu ses bonbons à l’érable, elle compose des sacs ayant des quantités différentes : un sac par quantité. Il est entendu que son frère lui demandera au moins 4 bonbons et au plus 15 bonbons. Elle devra pouvoir remplir la commande, peu importe le nombre de sacs livrés.

Au minimum, combien de sacs de quantités différentes Rosalie devra-t-elle préparer ?

                                                                                                                         Solutions 221 à 230

221. Croix de Clara

Clara a tracé la figure ci-après. Elle y a écrit un 5. Elle veut inscrire les nombres 6, 7, 8, 9, 10 et 11 dans les cases colorées. La somme doit être 24 dans chaque rangée de trois cases pas nécessairement accolées horizontalement, verticalement et en diagonale.

Distribuez les nombres.

222. Trottinette d’une souris

Une souris part du point gauche et se rend au point droit sans jamais revenir en arrière.

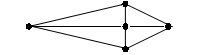
Combien la souris peut-elle emprunter de chemins différents.

223. Jetons de Samuel

Samuel prépare huit jetons et les numérote de 1 à 9, sauf 6. Il dessine la figure ci-après. Il place le jeton ayant le numéro 1 en bonne position.

Placez les autres jetons dans la grille de façon que la somme des numéros soit 15 dans chacune des rangées horizontales et verticales de trois cellules.

224. En toute amitié

Cinq couples se rencontrent. Chacun donne une poignée de mains aux autres, sauf à son conjoint ou à sa conjointe.

Combien y aura-t-il de poignées de mains ?

225. Jetons d’Alexandre

Alexandre dessine une grille 3 × 3. Il découpe huit jetons sur lesquels il écrit les lettres D, M, L, S, A, O, I, N ; puis, il dépose chaque jeton dans la grille de gauche comme il est indiqué.

Déplacez les jetons un à un sur toute case libre en les glissant horizontalement ou verticalement. À la fin, vous devez obtenir la disposition de la grille de droite.

226. Grille de Majorie

Majorie a placé les nombres de 17 à 25 dans la grille ci-après. Elle veut placer les nombres de 1 à 16 dans les cases vides de façon que la somme dans chaque ligne, chaque colonne et chaque diagonale soit égale à 65.

Distribuez les jetons de 1 à 16 dans les cases.

227. Dards de Damien

Damien place au mur le tableau ci-après. Il doit lancer trois dards sur le tableau de telle manière que la somme des numéros atteints soit 19.

Combien y a-t-il de groupes de trois cases qui satisfont à cette condition ?

228. Un anniversaire

Flavie est née le 18 juin 2012. Sa mère a décidé de confectionner un carré magique pour se remémorer cette journée. Sur la dernière ligne, elle a écrit 18, 06, 20, 12 dans cet ordre. À titre d’indices, elle a complété trois autres cases. La somme doit être la même sur chaque ligne, dans chaque colonne et dans chacune des deux diagonales.

Complétez le carré avec les nombres : 7, 9, 11, 13, 14, 15, 16, 19 et 21.

229. Dominos d’Albert

Albert a reçu en cadeau une boîte de dominos. Chaque domino est divisé en deux carrés marqués par des points dont les nombres représentent toutes les combinaisons possibles des entiers de 0 à 6 pris deux à deux. Le plus petit domino est le (0, 0) et le plus grand est le (6, 6).

Combien y a-t-il de dominos dans la boîte ?

230. Oméga de Marie

Dans la figure ci-après, Marie écrit 4, 8 et 9. Elle veut y placer les nombres 2, 5, 6, 7, 9 et 10. La somme doit être égale à 16 dans chaque rangée de deux ou de trois cases accolées.

Complétez la figure.

                                                                                                                         Solutions 231 à 240

231. Groupes de Claire

Claire a préparé la grille ci-après. Elle demande à son frère de former des groupes de trois nombres. Leur somme doit être 42 et l’un des nombres est la somme des deux autres.

Combien y a-t-il de tels groupes dans cette grille ?

232. Sablier de Louis

Louis, un ami de Marcel, a préparé le tableau suivant dans lequel il a dessiné un sablier.

Combien de fois peut-on lire MARCEL en accolant les lettres voisines ?

233. Jetons de Marika

Marika découpe cinq jetons et y écrit un nombre sur chacun : 2, 3, 4, 5 et 6. Elle prend deux jetons à la fois et multiplie les nombres qui y apparaissent.

Combien peut-elle compter de produits différents ?

234. Magie de Laurie

Laurie a placé trois nombres dans la grille ci-après. Elle veut y placer six autres nombres de façon que la somme soit la même dans chaque rangée horizontale, verticale et diagonale.

Complétez la grille.

235. Jetons de Vincent

Vincent a placé deux jetons dans la figure ci-après. L’un est marqué 7 et l’autre, 10. Il veut disposer les jetons de 2 à 8, sauf 3, de façon que la somme soit 20 dans chacune des quatre diagonales.

Distribuez les six autres jetons.

236. Lapins d’Océanne

Océanne a acheté 40 lapins. Elle place 5 lapins par enclos, soit 15 par côté. Au cours de la nuit, 4 lapins changent d’enclos. Pourtant, au matin, Océanne compte 16 lapins sur chaque côté de trois enclos.

Comment les lapins pouvaient-ils être répartis au matin ?

237. Billes de Doris

Doris a placé des billes dans neuf boîtes disposées comme ci-après. Il y a 54 billes dans chacune des rangées horizontales, verticales et diagonales. Doris a disposé 21 billes dans les boîtes B et E, puis cinq fois plus de billes dans la boîte A que dans la J. Tous les nombres sont divisibles par 3.

Combien y a-t-il de billes dans chaque boîte ?

238. Museaux de lapins

Lucie choisit 11 lapins pour leur mignon museau. Elle écrit sur chaque museau une lettre de A à K. Puis, elle place quatre lapins comme dans cette figure.

Disposez les sept autres lapins de façon que, si on additionne les rangs des lettres, la somme soit 17 dans chaque rangée de trois cases accolées.

239. Grille de Colette

Colette a écrit certains nombres de 1 à 25 dans la grille ci-après. La somme des nombres de chacune des 10 rangées de cinq nombres doit être 65.

Complétez la grille de telle manière que chaque nombre de 1 à 25 apparaît une fois.

240. Économie de Jeannot

Jeannot a 27 pièces de 5 ¢ et neuf pièces de 10 ¢. Julie lui demande de placer ses pièces dans neuf cases disposées en un carré.

1. Il doit y avoir neuf pièces de 5 ¢ dans chaque rangée horizontale, verticale et diagonale.

2. Il doit y avoir trois pièces de 10 ¢ dans chacune de ces rangées.

3. Dans la case A, Jeannot place quatre 5 ¢ et deux 10 ¢ ; tandis qu’il met trois 5 ¢ et deux 10 ¢ dans la case F.

Disposez les autres pièces.

                   FIN