Secrets des carrés magiques d'ordre 3

4.01 Déplacement des éléments
À partir d’un carré magique d’ordre 3, on peut trouver par rotation ou par symétrie d’autres carrés magiques. Ces carrés sont dits équivalents parce qu’ils sont obtenus par des déplacements.

n Par rotation : On fait tourner le carré magique successivement de 90° autour du médian.

1. Soit le carré magique ci-contre A1 qu’on appelle carré initial.

18	5	16
11	13	15
10	21	8

2. Ce deuxième carré A2 est obtenu par une rotation de 90° à partir de A1 dans le sens contraire des aiguilles d’une montre.

16	15	8
5	13	21
18	11	10

3. Ce troisième carré A3 est obtenu par une rotation de 90° à partir de A2 ou de 180° à partir de A1.

8	21	10
15	13	11
16	5	18

4. Ce quatrième carré est obtenu par une rotation de 90° à partir de A3, de 180° à partir de A2 ou de 270° à partir de A1.

10	11	18
21	13	5
8	15	16

Une nouvelle rotation de 90° donnerait le carré magique initial A1.

n Par symétrie : On déplace les éléments autour d’un axe qui peut être la deuxième ligne, la deuxième colonne, la diagonale de gauche ou la diagonale de droite.

5. On prend la deuxième ligne comme axe de symétrie. On intervertit les éléments des lignes 1 et 3. À partir de A1, on obtient A5 le carré ci-dessous.

10	21	8
11	13	15
18	5	16

On l’appelle carré interhorizontal de A1 et on le note A^h.

6. On prend la deuxième colonne comme axe. On obtient A6 le carré ci-dessous.

16	5	18
15	13	11
8	21	10

On l’appelle carré intervertical de A1 et on le note A^v.

7. On prend la diagonale de gauche comme axe. On obtient A7 le carré ci-dessous.

18	11	10
5	13	21
16	15	8

On l’appelle carré intergauche de A1 et on le note A^g.

8. On prend la diagonale de droite comme axe. On obtient A8 le carré ci-dessous.

8	15	16
21	13	5
10	11	18

On l’appelle carré interdroit de A1 et on le note A^d.

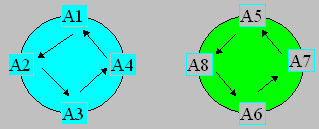
Les deux schémas suivants présentent les carrés magiques obtenus lorsque le déplacement se fait par rotation successive de 90°.

4.02 Relations entre les carrés magiques équivalents
Il existe des correspondances entre les carrés magiques équivalents obtenus par rotation et par symétrie.

Pour le carré magique interhorizontal : A^h

A5 est le carré magique interhorizontal de A1

A6 - - - - - - - - - - - - - - - - - - - - - - - A3

A7 - - - - - - - - - - - - - - - - - - - - - - - A2

A8 - - - - - - - - - - - - - - - - - - - - - - - A4

Pour le carré magique intervertical : A^v

A5 est le carré magique intervertical de A3

A6 - - - - - - - - - - - - - - - - - - - - - A1

A7 - - - - - - - - - - - - - - - - - - - - - A4

A8 - - - - - - - - - - - - - - - - - - - - - A2

Pour le carré magique intergauche : A^g

A5 est le carré magique intergauche de A4

A6 - - - - - - - - - - - - - - - - - - - - - A2

A7 - - - - - - - - - - - - - - - - - - - - - A1

A8 - - - - - - - - - - - - - - - - - - - - - A3

Pour le carré magique interdroit : A^d

A5 est le carré magique interdroit de A2

A6 - - - - - - - - - - - - - - - - - - - - A4

A7 - - - - - - - - - - - - - - - - - - - - -

Le schéma suivant représente de gauche à droite ou de droite à gauche les correspondances qui existent entre les différents carrés magiques équivalents.

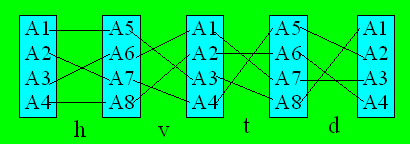
Exemple. (A1)^h = A5 ; (A5)^v = A3 ; (A3)^g= A8 ; (A8)^d = A1

ou (A1)^d = A8 ; (A8)^g= A3 ; (A3)^v = A5 ; (A5)^h = A1

4.03 Nombre de carrés magiques équivalents
Le nombre de carrés magiques équivalents varie selon le nombre d’éléments différents du carré magique.

1. Si le carré magique initial est formé de neuf éléments différents, alors on trouve huit carrés magiques équivalents comme il a été expliqué précédemment.

2. Si le carré magique initial est formé de sept éléments différents, on trouve également huit carrés magiques équivalents. En effet, même si deux éléments apparaissent deux fois, une même ligne ou une même colonne ne contient pas les mêmes éléments d’un carré magique à l’autre. Voici un exemple :

B1			B2			B3			B4
6	1	5	5	5	2	2	7	3	3	3	6
3	4	5	1	4	7	5	4	3	7	4	1
3	7	2	6	3	3	5	1	6	2	5	5

B5			B6			B7			B8
3	7	2	5	1	6	6	3	3	2	5	5
3	4	5	5	4	3	1	4	7	7	4	1
6	1	5	2	7	3	5	5	2	3	3	6

Les carrés B2, B3 et B4 sont formés par rotation de 90° à partir de B1. Les carrés B5, B6, B7 et B8 sont formés par symétrie à partir de B1.

3. Si le carré magique initial est formé de cinq éléments différents, on trouve quatre carrés magiques équivalents. Voici un exemple :

C1			C2			C3			C4
7	1	7	7	5	3	3	9	3	3	5	7
5	5	5	1	5	9	5	5	5	9	5	1
3	9	3	7	5	3	7	1	7	3	5	7

On obtient C2, C3, C4 par rotation successive de 90° à partir de C1.

En procédant par symétrie à partir de C1, on aura :

C1 et C6 sont identiques si l’axe est la deuxième colonne.

C2 et C7 sont identiques si l’axe est la première diagonale.

C3 et C5 sont identiques si l’axe est la deuxième ligne.

C4 et C8 sont identiques si l’axe est la deuxième diagonale.

4. Si le carré magique initial est formé de trois éléments différents, on trouve également quatre carrés magiques équivalents. Voici un exemple :

D1			D2			D3			D4
2	1	3	3	1	2	2	3	1	1	3	2
3	2	1	1	2	3	1	2	3	3	2	1
1	3	2	2	3	1	3	1	2	2	1	3

5. Si le carré magique initial est formé d’un seul élément, il n’existe pas de carré magique équivalent.

En résumé, on aura le tableau suivant :

Éléments différents	9	7	5	3	1
Carrés magiques	8	8	4	4	1

4.04 Densité des carrés magiques équivalents
La densité du carré magique interhorizontal, intervertical, intergauche ou interdroit de A est égale à la densité de A. On peut écrire les identités suivantes.

d(A^h) = d(A)

d(A^v) = d(A)

d(A^g) = d(A)

d(A^d) = d(A)

On sait que A^h, A^v, A^gou A^d sont des carrés magiques équivalents à A. Or, deux carrés magiques équivalents sont nécessairement colinéaires. Donc, ces carrés magiques ont la même densité. Exemple 1. Soit A le carré ci-dessous,

35	10	30
20	25	30
20	40	15

d(A^h) = 75 d(A^v) = 75 d(A^t) = 75 d(A^d) = 75

Exemple 2. Calculez la densité de 4A^h + 7B^v si d(A) = 5 et d(B) = 8

On fait :

d(4A^h + 7B^v)

4d(A^h) + 7d(B^v)

4d(A) + 7d(B)

20 + 56 = 76

4.05 Somme du carré interhorizontal et intervertical
La somme du carré magique interhorizontal de A et intervertical de A est égale à un carré magique homogène dont la base est le double du médian de A.

Soit A le carré ci-dessous,

a₁	a₂	a₃
a₄	a₅	a₆
a₇	a₈	a₉

On aura :

a₇	a₈	a₉	+	a₃	a₂	a₁
a₄	a₅	a₆		a₆	a₅	a₄
a₁	a₂	a₃		a₉	a₈	a₇

=	a₃+a₇	a₂ + a₈	a₁ + a₉
	a₄ + a₆	2a₅	a₄ + a₆
	a₁ + a₉	a₂ + a₈	a₃ + a₇

Dans A, a₁ + a₉ = a₃ + a₇ = a₂ + a₈ = a₄ + a₆= 2a₅

Par ailleurs, a₁ + a₅ + a₉ = d(A)

a₁ + a₅ + a₉ = 3a₅

a₁ + a₉ = 2a₅

Donc, a₁ + a₉ = a₃ + a₇ = a₂ + a₈ = a₄ + a₆_.

Exemple. Soit A =

47	15	61
55	41	27
21	67	35

Alors A^h + A^vest le carré homogène ci-dessous.

82	82	82
82	82	82
82	82	82

La somme du carré magique intergauche de A et interdroite de A est aussi égale à un carré magique homogène dont la base est le double du médian de A. D’où, on peut écrire : A^h + A^v = A^g+ A^d.

4.06 Carré magique interhorizontal d’une somme
Le carré magique interhorizontal de la somme de deux carrés magiques est égal à la somme des deux carrés magiques interhorizontaux. On peut écrire : (A + B)^h = A^h + B^h.

Il en est de même pour tout carré magique intervertical, intergauche et interdroit comme on le voit dans ces trois identités.

(A + B)^v = A^v + B^v

(A + B)^g= A^g+ B^t

(A + B)^d = A^d+ B^d

Exemple. Soit A et B deux carrés magiques,

8	15	10	30	5	25
13	11	9	15	20	25
12	7	14	15	35	10

(A + B)^v =

A^v + B^v =	10	15	8	+	25	5	30	=	35	20	38
	9	11	13		25	20	15		34	31	28
	14	7	12		10	35	15		24	42	27

4.07 Carré magique homogène
Le carré magique interhorizontal, intervertical, intergauche ou interdroit d’un carré magique homogène est égal au carré magique homogène initial.

K^h = K, K^v = K, K^g= K, K^d = K

Exemple. Soit K un carré magique homogène,

8	8	8
8	8	8
8	8	8

alors K^h = K^v= K^g= K^d= K

4.08 Produit d’un scalaire et d’un carré magique
Le carré magique interhorizontal, intervertical, intergauche et interdroit du produit d’un scalaire k et d’un carré magique A est respectivement égal au produit du scalaire k et du carré magique interhorizontal, intervertical, intergauche et interdroit de A. On peut écrire les quatre identités suivantes.

(kA)^h = kA^h.

(kA)^v = kA^v

(kA)^g= kA^g

(kA)^d = kA^d

Exemple. Soit le carré magique A,

40	9	38
27	29	31
20	49	18

Alors,

(3A)^g=

120

114

120

= 3

147

114

4.09 Double symétrie
Lorsqu'on fait une double symétrie sur un carré magique, on obtient les relations suivantes :

1) (A^h)^h = (A^v)^v = (A^g)^g= (A^d)^d = A

2) (A^h)^v = (A^v)^h = (A^g)^d = (A^d)^g

3) (A^h)^g= (A^v)^d = (A^g)^v = (A^d)^h

4) (A^h)^d = (A^v)^g= (A^g)^h = (A^d)^v

Exemple 1. Soit A le carré,

8	25	12
19	15	11
18	5	22

Alors,

(A^h)^h =

= A

Exemple 2. Soit A le carré,

70	10	55
30	45	60
35	80	20

Alors,

(A^h)^v =

et (A^v)^h =