Les deux premiers treillis ci-après sont constitués chacun de trois cercles et le troisième d’un cercle et de deux ellipses. Ils reçoivent les entiers de 1 à 6 répartis en quadruplets : (1, 2, 5, 6), (1, 3, 4, 6) et (2, 3, 4, 5). Leur densité est 14. Selon la classification proposée dans l’article Treillis magiques, ces trois treillis peuvent être codés 6-4-3-60-1a, 6-4-3-60-1b et 6-4-3-60-1c. 

Les trois treillis suivants sont isomorphes aux précédents. Les rangées du premier sont deux cercles et un diamètre prolongé ; le deuxième un carré et deux trapèzes isocèles; le troisième un carré et deux flèches.

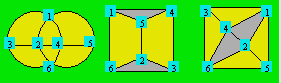
Pour rendre magiques les treillis de cette classe, on peut partager les éléments en paires de nombres complémentaires dont la somme est (n² - n + 1). Dans les exemples donnés, comme n = 3, la somme est 7. Les paires de complémentaires sont (1, 6), (2, 5) et (3, 4), tout comme dans le dé hexaédrique.

2^e Treillis constitué de n cercles concentriques et de m diamètres. Voici quatre situations différentes :

n n est égal à m
Les points d’intersection ou cellules reçoivent des nombres répartis de telle manière que leur somme appelée densité est la même dans chaque rangée (cercle et diamètre). Sous sa forme normale, un tel treillis reçoit les entiers de 1 à 2n², soit le double d’un carré ou la demie de deux triangulaires successifs. 

Pour trouver la densité, on fait la somme des entiers de 1 à 2n² ; puis on divise par n. La densité est égale à n(2n² + 1). Par rapport au nombre de cellules c, la densité est n(c + 1). Le tableau suivant donne le nombre de cellules et la densité pour chaque treillis quand n varie de 1 à 8.

Le treillis de gauche ci-après est constitué de trois cercles et de trois diamètres. Il reçoit les entiers de 1 à 18. Sa densité est 57. Le treillis de droite est composé de trois carrés et de trois droites : deux diagonales et une médiatrice. Les deux treillis sont isomorphes. Ils peuvent être classés 18-6-6-180-1a et 18-6-6-180-1b.

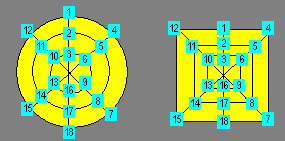
Pour rendre magiques les treillis de cette classe, on peut partager les éléments en paires de nombres complémentaires dont la somme est (2n² + 1) ou le nombre de cellules plus 1’unité. Dans ce cas, comme n = 3, la somme est 19. Les paires de complémentaires sont (1, 18), (2, 17), (3, 16), etc. On place les deux éléments d’une paire sur les deux points d’intersection d’un cercle et d’un diamètre. 

Seki Kowa a donné un treillis normal de cette classe constitué de cinq cercles concentriques dont la somme est 265 sur chacun des cercles et 266 sur chacun des diamètres.

n m est égal à (n + 1)
Le treillis comprend n(n + 1) rangées. Les points d’intersection ou cellules reçoivent des nombres répartis de telle manière que leur somme appelée densité est la même dans chaque rangée. 

Sous sa forme normale, un tel treillis comporte les entiers de 1 à (2n² + 2n + 1), soit un nombre gnomonique octaédrique ou un centré D2 carré. La densité est égale à (n + 1)(2n² + 2n + 1). Par rapport au nombre de cellules c, la densité est (n + 1)c. Le tableau suivant donne le nombre de cellules et la densité pour chaque treillis quand n varie de 1 à 7.

Le treillis de gauche ci-après est constitué de deux cercles et de trois diamètres, soit 2 ´ 3 rangées. Il reçoit les entiers de 1 à 13. Sa densité est 39. Le treillis de droite est composé de deux carrés et de trois droites (deux diagonales et une médiatrice). Il est isomorphe au premier.

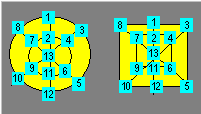
Pour rendre magiques les treillis de cette classe, on peut partager les éléments en paires de nombres complémentaires dont la somme est (2n² + 2n + 1). Dans ce cas, comme n = 2, la somme est 13. Les paires complémentaires sont (1, 12), (2, 11), (3, 10), etc. On place les deux éléments d’une paire sur les deux points d’intersection d’un cercle et d’un diamètre. Comme chaque cercle supporte six éléments et chaque diamètre cinq éléments, soit un de moins, on doit placer la somme des complémentaires au centre du treillis pour que chaque rangée ait la même somme, soit une densité unique. C’est un treillis normal.

n m est plus grand ou égal à (n + 2)
Les points d’intersection ou cellules reçoivent des nombres répartis de telle manière que leur somme est la même d’une part sur chaque cercle et d’autre part sur chaque diamètre. Ces sommes sont proportionnelles au nombre de cellules par rangée. Soit un treillis n ´ (n + 2), sous sa forme normale, il comporte les entiers de 1 à 2n(n + 2). La somme sur chaque cercle est (n + 2) (c + 1); la somme sur chaque diamètre est n(c + 1) où c est mis pour le nombre total de cellules. 

Ainsi, dans un treillis 2 ´ 4, la somme est 17 ´ 4 = 68 sur chaque cercle et 17 ´ 2 = 34 sur chaque diamètre. Le tableau suivant donne le nombre de cellules, la somme des cercles et celle des diamètres quand n varie de 1 à 7.

Le treillis de gauche ci-après est d’ordre 2 ´ 4. Il est constitué de deux cercles et de quatre diamètres. Il reçoit les entiers de 1 à 16. Le treillis de droite est composé de deux carrés et de trois droites : deux diagonales et une médiatrice. Les deux treillis sont isomorphes l’un à l’autre.

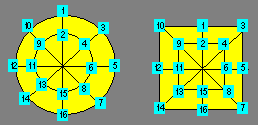
Pour rendre magiques les treillis de cette classe, on peut partager les éléments en paires de nombres complémentaires dont la somme est (2n² + 4n + 1). Dans ce cas, comme n = 2, la somme est 17. Les paires complémentaires sont (1, 16), (2, 15), (3, 14), etc. On place les deux éléments d’une paire sur les deux points d’intersection d’un cercle et d’un diamètre. La somme est 68 sur chaque cercle et 34 sur chaque diamètre. Le treillis est normal, car il contient les éléments de 1 à 16. Pour avoir une densité unique, on n’aurait qu’à ajouter 34 au centre du treillis, mais le treillis ne serait pas normal.

n n est plus grand que m
Comme dans le cas précédent, il n’y a pas de densité unique ; mais les sommes sont proportionnelles au nombre de cellules par rangée. Voici trois exemples :

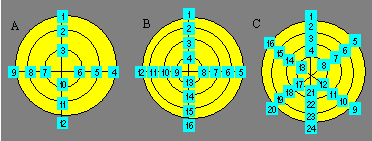
Le tableau suivant donne pour chaque treillis le nombre de cercles, le nombre de diamètres de même que leur somme particulière.

3^e Treillis constitué de n cercles concentriques et de m rayons. Voici deux situations différentes :

n n est égal à m
Les points d’intersection ou cellules reçoivent des nombres répartis de telle manière que leur somme appelée densité est la même dans chaque rangée (cercle et rayon). Un tel treillis sous sa forme normale reçoit les entiers de 1 à n². Pour trouver la densité, on fait la somme des entiers de 1 à n², puis on divise par n. La densité est égale à n(n² + 1)/2. Par rapport au nombre de cellules c, la densité est n(c + 1)/2. 

Le tableau suivant donne le nombre de cellules et la densité pour chaque treillis quand n varie de 3 à 10.

Voici trois treillis normaux constitués de 3, 4, 5 cercles et d’autant de rayons :

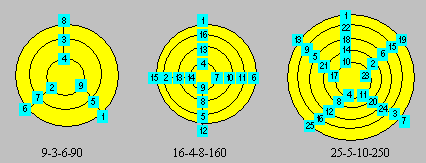
Le code de chaque treillis est donné. Les treillis de cette classe sont isomorphes aux carrés magiques d’ordre n sans considération des diagonales.

n n est différent de m
Une somme existe sur chaque cercle et une autre sur chaque rayon. Ces sommes sont proportionnelles au nombre de cellules par rangée. Dans la configuration de gauche ci-après, la somme est 32 sur chaque cercle et 24 sur chaque rayon. Dans l’autre configuration, elle est 75 sur chaque cercle et 50 sur chaque rayon.

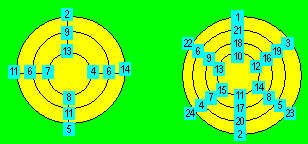
Ces derniers treillis sont isomorphes aux rectangles magiques. On pourrait considérer deux rayons en ligne comme un diamètre.

Les cercles magiques ont été inventés par Benjamin Franklin (1706-1790).