Ensemble de termes qui se succèdent dans un ordre déterminé et qui se déduisent généralement les uns des autres selon des règles précises. Voici deux suites :

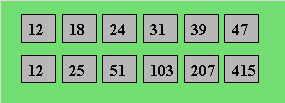
La règle de la première suite est : additionner 5 au nombre précédent, puis additionner le chiffre de la dizaine. La règle de la seconde est : multiplier le nombre précédent par 2, puis additionner le chiffre de l'unité. On peut représenter une suite par un graphe selon la méthode dichromatique à la condition de prendre uniquement les deux derniers chiffres de la suite, lorsqu'il y en a plus.

On peut additionner terme à terme deux suites. Par exemple, si on additionne les termes de la suite des nombres impairs : 1, 3, 5, 7, 9, 11, 13, 15, ... à la suite des nombres carrés : 1, 4, 9, 16, 25, 36, 49, 64 ... on obtient la suite : 2, 7, 14, 23, 34, 47, 62, 79 ... La différence entre chacun des termes successifs de cette dernière est : 5, 7, 9, 11, 13, 15, 17. 

Une suite peut être aléatoire, aliquote, arithmétique, joyeuse ou magique. On connaît la suite de Fibonacci, celle de Langford et celle de Lucas. 

Une suite d'entiers consécutifs disposés en un triangle est appelée triangle de Kordiemsky. Des suites  apparaissent parfois dans les tests d'intelligence. Les problèmes de suite appartiennent à la classe des récréations numériques.

© Charles-É. Jean

Index : S

Voir aussi Suite dans l'Aide-mémoire.