En guise de conclusion

Fête des mathématiques

***********

Chapitre 1. Objets ludiques

1.01 Tout en œufs

Dans la littérature récréative mathématique, on trouve des situations où des moitiés d’œufs sont distribuées sans casser aucun œuf. Cela semble relever de la magie. Il n’en est rien. Si on a un nombre impair d’œufs, la moitié est un entier plus une fraction qui est la moitié. Quand on s’astreint à donner en plus une moitié, cela revient à distribuer un œuf entier.

Problème 1

Le premier problème connu dans cette catégorie est attribué à Frédéric Ozanam (1640-1717). Le voici :

Une femme de campagne porte des œufs au marché dans une ville de guerre où il y a trois corps de garde à passer. Au premier, elle laisse la moitié de ses œufs et la moitié d'un ; au second, la moitié de ce qui lui restait et la moitié d'un ; au troisième, la moitié de ce qui lui restait et la moitié d'un ; enfin, elle arrive au marché avec trois douzaines.

Comment cela se peut-il faire sans rompre aucun œuf ? Solution 1.01-1

Problème 2

Le calculateur prodige Henri Mondeux (1826-1861) a formulé un autre problème sur le même modèle mathématique :

Une marchande d'œufs va au marché avec une certaine quantité d'œufs. À une première personne, elle vend la moitié de ses œufs, plus la moitié d'un œuf ; à une deuxième, la moitié de ce qu'il lui reste, plus la moitié d'un œuf, et de même à une troisième et à une quatrième personne. Alors elle a tout vendu et elle n'en a cassé aucun.

Combien avait-elle d’œufs en arrivant au marché ?

Démarche 1. On procède par tâtonnement.

Au départ, on doit choisir un nombre impair d’œufs. Imaginons que la marchande avait 27 œufs. Elle en vend 13 ½ + ½ = 14. Il lui en reste 13. Elle en vend 6 ½ + ½ = 7. Il lui en reste 6. On ne peut pas continuer car 6 est pair. Pour que chaque vente puisse se réaliser, il faut qu’il reste toujours un nombre impair d’œufs. C’est ce que nous apprend cette première démarche. Toutefois, il semble plus raisonnable d’abandonner le tâtonnement, car on pourrait chercher longtemps.

Démarche 2. On procède à rebours

On cherche le nombre d’œufs vendus depuis la fin. Observons ce qui se passe si on avait 6 œufs à la fin comme il est trouvé dans la démarche précédente. À rebours, on fait : (6 + ½)2 = 13, puis (13 + ½)2 = 27. On multiplie par 2 car l’inverse de la moitié est le double.

Maintenant, partons de 0.

À la quatrième personne, la marchande aura vendu 1 œuf. En effet, (0 + ½)2 = 1.

À la troisième personne, la marchande aura vendu 3 œufs. En effet, (1 + ½)2 = 3.

À la deuxième personne, la marchande aura vendu 7 œufs. En effet, (3 + ½)2 = 7.

À la première personne, la marchande aura vendu 15 œufs. En effet, (7 + ½)2 = 15.

La marchande a vendu 15 œufs.

Démarche 3. On procède à rebours (bis)

On cherche le nombre d’œufs vendus à chaque transaction en commençant par la fin. Comme il reste 0 œuf, la quatrième vente est d’un œuf. Par la suite, le nombre d’œufs vendus double à chaque vente. On aura successivement 1, 2, 4, 8 œufs vendus : ce qui fait un total de 15.

La marchande a vendu 15 œufs.

Démarche 4. On procède par induction.

Cette démarche est principalement nécessaire quand les ventes sont relativement nombreuses. Par exemple, supposons que le nombre n de ventes est 25. En se basant sur les données de la deuxième démarche où n représente le nombre de ventes, on peut écrire :

Si n = 1, on vend 1 œuf.

Si n = 2, on vend 3 œufs.

Si n = 3, on vend 7 œufs.

Si n = 4, on vend 15 œufs.

Pour trouver le nombre d’œufs d’une vente à l’autre, on multiplie par 2 le nombre d’œufs précédent et on additionne 1. Par exemple, pour n = 4, on fait 7 × 2 + 1 = 15.

Pour arriver au résultat total sans passer par ces étapes, on élève 2 à la puissance n et on soustrait 1. Par exemple, si n = 4, on fait : 2⁴ – 1 = 15.

La marchande a vendu 15 œufs.

Si n = 25, la marchande aura vendu (2²⁵ – 1) œufs, soit 33 554 431 œufs. On suppose que la marchande manipule un œuf à la seconde, le tout prendrait approximativement un an et 23 jours. Surprenant, n’est-ce pas ?

Problème 3

Une marchande vend à une première personne le tiers de ses œufs plus le tiers d’un œuf ; à une seconde personne le tiers de ce qui lui reste plus le tiers d’un œuf ; enfin, à une troisième personne le tiers de ce qui lui reste plus le tiers d’un œuf. Après cette troisième vente, il lui reste 7 œufs.

Combien la marchande avait-elle d’œufs en arrivant au marché ? Solution 1.01-3

* * * * * * *

1.02 Dons de caramels

Problème 1

France dit à Gratien :

« Si tu me donnais 10 de tes caramels, j’en aurais le double de toi ».

Gratien reprend :

« Si tu me donnais 8 de tes caramels, j’en aurais le double de toi ».

Combien chacun a-t-il de caramels ?

Démarche 1. Utilisation de tableaux

Si France avait 2 caramels, Gratien en aurait 16. Si France avait 4 caramels, Gratien en aurait 17. Si France avait 6 caramels, Gratien en aurait 18, etc. On écrit les données dans le tableau.

Si Gratien avait 2 caramels, France en aurait 13. Si Gratien avait 4 caramels, France en aurait 14. Si Gratien avait 6 caramels, France en aurait 15, etc.

Dans le premier tableau, on note que les quantités attribuées à France augmentent de 2. Celles attribuées à Gratien augmentent de 1. Dans le second tableau, c’est l’opposé qui se produit. On arrête d’écrire les données dans les tableaux quand on aperçoit les deux mêmes nombres d’un tableau à l’autre dans une colonne.

France a 26 caramels et Gratien en a 28.

Démarche 2. À l’aide de l’algèbre

France a x caramels. Elle en reçoit 10 de Gratien. Elle en a (x + 10). Gratien a y caramels. Il en donne 10 à France. Il en a (y – 10). Comme France en a le double de Gratien, pour avoir une égalité, il faut multiplier par 2 l’avoir de Gratien. L’équation est : x + 10 = 2(y – 10).

On fait le même raisonnement concernant les paroles de Gratien. L’équation est : 2(x – 8) = y + 8. On résout les deux équations. On trouve x = 26 et y = 28.

France a 26 caramels et Gratien en a 28.

Démarche 3. On généralise

Soit x le nombre de caramels de France et y celui de Gratien. Soit f le don de France et g le don de Gratien. On peut écrire : x + g = 2(y – g) et 2(x – f) = y + f. On résout les deux équations. On obtient : x = 2f + g et y = f + 2g.

Or, dans l’énoncé, f = 8 et g = 10. D’où, x = 26 et y = 28.

France a 26 caramels et Gratien en a 28.

Problème 2

France dit à Gratien :

« Si tu me donnais 15 de tes caramels, j’en aurais le double de toi ».

Gratien reprend :

« Si tu me donnais 11 de tes caramels, j’en aurais le double de toi ».

Combien chacun a-t-il de caramels ?

Maintenant qu’on est familier avec ce genre de problèmes, on peut trouver d’autres démarches. En voici quatre :

Démarche 1

• On additionne le don de Gratien et deux fois le don de France : c’est l’avoir de France.

• On additionne le don de France et deux fois le don de Gratien : c’est l’avoir de Gratien.

On fait : 15 + 2 × 11 = 37, puis 11 + 2 × 15 = 41.

France a 37 caramels et Gratien en a 41.

Démarche 2

• On additionne les dons.

• On multiplie par 2.

• Du résultat, on soustrait le don de Gratien : c’est l’avoir de France.

• Du résultat, on soustrait le don de France : c’est l’avoir de Gratien.

On fait : 15 + 11 = 26, 26 × 2 = 52, 52 – 15 = 37 et 52 – 11 = 41.

France a 37 caramels et Gratien en a 41.

Démarche 3

• On additionne les dons.

• On multiplie par 1,5.

• On soustrait la moitié de la différence des dons : c’est l’avoir de France.

• On additionne la moitié de la différence des dons : c’est l’avoir de Gratien.

On fait : 15 + 11 = 26, 26 × 1,5 = 39, 15 – 11 = 4, 4 ÷ 2 = 2, 39 – 2 = 37 et 39 + 2 = 41.

France a 37 caramels et Gratien en a 41.

Démarche 4

• On additionne les dons et on multiplie par 3.

• On soustrait les dons.

• On additionne les deux résultats et on divise par 2 : c’est l’avoir de Gratien.

• On soustrait les deux résultats et on divise par 2 : c’est l’avoir de France.

On fait : 15 + 11 = 26 et 26 × 3 = 78. On fait : 15 – 11 = 4, 78 + 4 = 82, 82 ÷ 2 = 41, 78 – 4 = 74, 74 ÷ 2 = 37.

France a 37 caramels et Gratien en a 41.

Problème 3

France dit à Gratien :

« Si tu me donnais 3 de tes caramels, j’en aurais le triple de toi ».

Gratien reprend :

« Si tu me donnais 2 de tes caramels, j’en aurais autant que toi ».

Combien chacun a-t-il de caramels ? Solution 1.02-3

* * * * * * *  

1.03 Médaillons à problèmes

Problème 1

Roméo a un certain nombre de médaillons. À l’aîné de ses enfants, il en donne la moitié. Au deuxième, il donne la moitié de ce qui lui reste. Au troisième, il donne encore la moitié de ce qui lui reste. Il possède encore 20 médaillons.

Combien Roméo avait-il de médaillons ?

Démarche 1

À la fin, il reste 20 médaillons. On fait : 20 × 2 = 40.

Il reste 40 médaillons. On fait : 40 × 2 = 80.

Il reste 80 médaillons, On fait : 80 × 2 = 160.

Roméo avait 160 médaillons.

Démarche 2

Au troisième, Roméo donne 20 médaillons. Il avait donc 40 médaillons.

Au deuxième, Roméo donne 40 médaillons. Il avait donc 80 médaillons.

Au troisième, Roméo donne 80 médaillons.

Il a donné 140 médaillons, soit 20 + 40 + 80. À la fin, il lui en reste 20. On fait : 140 + 20 = 160.

Roméo avait 160 médaillons.

Démarche 3

Procédons par induction. Cette démarche serait essentielle si le nombre de personnes était très grand.

Soit n le nombre de médaillons qui restent à Roméo. Examinons les cas où n varie de 1 à 3 en procédant à rebours.

n = 1

À la fin, il reste 1 médaillon à Roméo. Au troisième, il donne 1 médaillon. Au deuxième, 2 médaillons. Au premier, 4 médaillons. Il avait 8 médaillons.

n = 2

À la fin, il reste 2 médaillons à Roméo. Au troisième, il donne 2 médaillons. Au deuxième, 4 médaillons. Au premier, 8 médaillons. Il avait 16 médaillons.

n = 3

À la fin, il reste 3 médaillons à Roméo. Au troisième, il donne 3 médaillons. Au deuxième, 6 médaillons. Au premier, 12 médaillons. Il avait 24 médaillons.

À la fin, Roméo possède n médaillons. Au troisième, il donne n médaillons, au deuxième 2n médaillons et au premier 4n médaillons. Il avait 8n médaillons. On fait : 20 × 8 = 160.

Roméo avait 160 médaillons.

Problème 2

Reine donne la moitié de ses médaillons, plus 1, successivement à ses trois enfants. À la fin, il lui reste 4 médaillons.

Combien Reine avait-elle de médaillons ? Solution 1.03-2

Problème 3

Roméo a un certain nombre de dés. À l’aîné de ses enfants, il donne le tiers de ses dés, plus 1. Au deuxième, il donne le tiers des dés qui lui restent, plus 1. Au troisième, il donne les 9 dés qui lui restent.

Combien Roméo avait-il de dés ? Solution 1.03-3

Problème 4

Élodie dépense chaque jour la moitié de ce qu’elle possédait, plus 1 $. Après quatre jours, elle a tout dépensé.

Quelle somme avait-elle ? Solution 1.03-4

* * * * * * *  

1.04 Des neveux et des nièces

Problème 1

Dorothée, Françoise et Gaétane sont trois sœurs. Dorothée a 3 neveux. Françoise a 6 neveux. Gaétane a 5 neveux.

Combien chacune a-t-elle de fils ?

Démarche 1

Soit d le nombre de fils de Dorothée, f celui de Françoise, g celui de Gaétane. On écrit :

f + g = 3

d + g = 6

d + f = 5

On additionne les trois équations. On obtient : 2d + 2f + 2g = 14. En simplifiant, on a : d + f + g = 7. Puisque f + g = 3, alors d = 4. Puisque d + g = 6, alors f = 1. Puisque d + f = 5, alors g = 2.

Dorothée a 4 fils. Françoise a 1 fils. Gaétane a 2 fils.

Démarche 2

• On additionne les nombres de neveux.

• On divise par 2.

• Du résultat, on soustrait chaque nombre de neveux.

On fait : 3 + 6 + 5 = 14, 14 ÷ 2 = 7, 7 – 3 = 4 (Dorothée), 7 – 6 = 1 (Françoise) et 7 – 5 = 2 (Gaétane).

Dorothée a 4 fils. Françoise a 1 fils. Gaétane a 2 fils.

Problème 2

Marcel, Normand, Pierre et Quentin sont quatre frères. Marcel a 8 nièces. Normand a 7 nièces. Pierre a 9 nièces. Quentin a 6 nièces.

Combien chacun a-t-il de filles ?

Démarche 1

Soit m le nombre de filles de Marcel, n celui de Normand, p celui de Pierre et q celui de Quentin. On écrit :

n + p + q = 8

m + p + q = 7

m + n + q = 9

m + n + p = 6

On additionne les quatre équations. On obtient : 3m + 3n + 3p + 3q = 30. En simplifiant, on a : m + n + p + q = 10. Puisque n + p + q = 8, alors m = 2. Puisque m + p + q = 7, alors n = 3. Puisque m + n + q = 9, alors p = 1. Puisque m + n + p = 6, alors q = 4.

Marcel a 2 filles. Normand a 3 filles. Pierre a 1 fille. Quentin a 4 filles.

Démarche 2

• On additionne les nombres de nièces.

• On divise par 3.

• Du résultat, on soustrait chaque nombre de nièces.

On fait : 8 + 7 + 9 + 6 = 30, 30 ÷ 3 = 10, 10 – 8 = 2 (Marcel), 10 – 7 = 3 (Normand), 10 – 9 = 1 (Pierre), 10 – 6 = 4 (Quentin).

Marcel a 2 filles. Normand a 3 filles. Pierre a 1 fille. Quentin a 4 filles.

Problème 3

Bernard, Cyprien, Danick, Ernest et Félicien sont cinq frères. Bernard a 10 nièces. Cyprien a 8 nièces. Danick a 7 nièces. Ernest a 9 nièces. Félicien a 10 nièces.

Combien chacun a-t-il de filles ? Solution 1.04-3

* * * * * * *

1.05 Un rectangle de sous

Problème 1

Anne place 6 sous en un rectangle 2 × 3. Puis, elle entoure le rectangle d’une première couronne. Cette dernière nécessite 14 pièces.

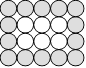
Combien de pièces seront nécessaires pour former une cinquième couronne ?

Démarche 1

La démarche qui nous vient d’abord à l’esprit est de former les couronnes en dessinant les sous. Cela risque d’être long et fastidieux, sans compter les risques d’erreurs.

Démarche 2

 On peut prendre des sous ou des jetons. Le risque d’erreurs est diminué.

Démarche 3

On peut faire un tableau où R est le rang de la couronne, H1, la rangée horizontale supérieure, H2, la rangée horizontale inférieure, C1 la première colonne, sauf les sous déjà comptés, et C2 la dernière colonne, sauf les sous déjà comptés. Pour chaque rangée, on donne le nombre de sous nécessaires.

On remarque que d’une couronne à l’autre, le nombre de sous augmente de 2 dans chaque rangée : ce qui fait une augmentation de 8 au total.

La cinquième couronne nécessite 46 sous.

Démarche 4

Le rectangle initial est de 2 × 3. Il nécessite 6 sous.

La première couronne est dans un rectangle 4 × 5. Celui-ci contient 20 sous. On soustrait 6 et on obtient 14.

La deuxième couronne est dans un rectangle 6 × 7. Celui-ci contient 42 sous. On soustrait 20 et on obtient 22.

La troisième couronne est dans un rectangle 8 × 9. Celui-ci contient 72 sous. On soustrait 42 et on obtient 30.

La quatrième couronne est dans un rectangle 10 × 11. Celui-ci contient 110 sous. On soustrait 72 et on obtient 38.

La cinquième couronne est dans un rectangle 12 × 13. Celui-ci contient 156 sous. On soustrait 110 et on obtient 46.

La cinquième couronne nécessite 46 sous.

Problème 2

Combien de pièces seront nécessaires pour former une 100^e couronne ?

Démarche

D’une couronne à l’autre, le nombre de sous augmente de 8. On peut trouver et appliquer une formule. Le nombre de sous d’une couronne est égal à 8x + 6 où x est le rang de la couronne. Comme x = 100, on fait : 8 × 100 + 6 = 806.

La 100^e couronne nécessite 806 sous.

Problème 3

Nathan place 15 sous en un rectangle 3 × 5. Puis, il entoure le rectangle d’une première couronne.

Combien de sous seront nécessaires pour former une troisième couronne ? Solution 1.05-3

* * * * * * *

1.06 Folles dépenses

Problème 1

Mélodie dépense chaque jour la moitié de ce qu’elle possédait, plus 2 $. Après quatre jours, elle a tout dépensé.

Quelle somme avait-elle ?

Démarche 1. On procède par tâtonnement.

On suppose que Mélodie avait 54 $. Le premier jour, elle dépense d’abord 27 $, puis 2 $, ce qui fait une dépense de 29 $. Il lui reste : 54 – 29 = 25 $. Le deuxième jour, elle dépense 12,50 $ plus 2 $. Il lui reste 10,50 $. Il faut que le montant restant soit un nombre pair. Autrement, on aboutit toujours à des sous.

On suppose que Mélodie a 56 $. On fait : (56 – 4)/2 = 26. Il lui reste 26 $. On fait : (26 – 4)/2 = 11. Il lui reste 11 $. Ce montant ne peut pas être impair.

Cette démarche peut exiger un temps considérable. Toutefois, même si elle ne donne pas de résultat comme c’est le cas ici, elle a l’avantage de nous aider à préciser une démarche à suivre.

Démarche 2. On procède par régression.

Une condition connue, c’est le 0 $ de la fin. Procédons du connu à l’inconnu, soit par régression ou à rebours. On doit transformer les données par des opérations inverses. La soustraction devient une addition. La division devient une multiplication. Précédemment, on soustrayait 4 et on divisait par 2. Dans le cas de la régression, on multiplie par 2 et additionne 4.

Quatrième jour : 0

Troisième jour : 0 × 2 + 4 = 4

Deuxième jour : 4 × 2 + 4 = 12

Premier jour : 12 × 2 + 4 = 28

Auparavant : 28 × 2 + 4 = 60

Mélodie avait 60 $. Elle dépense 32 $ le premier jour. Il lui en reste 28. Elle dépense 16 $ le deuxième jour. Il lui en reste 12. Elle dépense 8 $ le troisième jour. Il lui en reste 4. Elle dépense 4 $ le quatrième jour. Il lui en reste 0.

Démarche 3. On généralise.

Dans le premier cas, pour passer de 54 $ à 25 $, on pouvait faire : (54 – 4)/2 = 25. Si on remplace 54 par n, on peut écrire (n – 4)/2.

On écrit : (n – 4)/2 = 0 qui est le montant final. D’où n = 4.

On écrit : (n – 4)/2 = 4 qui est le montant précédent. D’où n = 12.

On écrit : (n – 4)/2 = 12 qui est le montant précédent. D’où n = 28.

On écrit : (n – 4)/2 = 28 qui est le montant précédent. D’où n = 60.

Mélodie avait 60 $.                                                         

Démarche 4. On utilise les propriétés des suites.

Le quatrième jour, Mélodie a 0 $. On fait : 0 × 2 + 4 = 4 comme dans la deuxième démarche. Le troisième jour, Mélodie a 4 $. La différence pour les deux jours est 4. On multiplie successivement par 2. Les différences seront : 8, 16, 32. On peut écrire : 4 + 8 = 12, 12 + 16 = 28 et 28 + 32 = 60.

Mélodie avait 60 $.

Démarche 5. On procède par un tableau.

Les montants successifs m sont 0, 4, 12, 28. Les différences successives d sont 4, 8, 16, 32. En faisant la somme, on obtient le total pour chaque jour. Voici le tableau :

Dans le coin inférieur droit, on trouve 60. Mélodie avait 60 $.

Démarche 6. On procède de façon algébrique.

Soit x la somme que Mélodie avait. Le premier jour, il restera (x – 4)/2 à Mélodie. Pour le deuxième jour, on remplace x par (x – 4)/2 et on simplifie, on obtient (x – 12)/4. Pour le troisième jour, on remplace le dernier x par (x – 4)/2 et on simplifie, on obtient (x – 28)/8. Pour le quatrième jour, on remplace encore le dernier x par (x – 4)/2 et on simplifie, on obtient (x – 60)/16.

On pose : (x – 60)/16 = 0. D’où, x = 60. Mélodie avait 60 $.

Problème 2

Élodie dépense chaque jour la moitié de ce qu’elle possédait plus 1 $. Après quatre jours, elle a tout dépensé.

Quelle somme avait-elle au début ? Solution 1.06-2

* * * * * * *

1.07 Cartes en symboles

Problème 1

Antoine dessine des symboles du jeu de cartes. Il représente successivement des cœurs, des trèfles et des piques en augmentant d’un symbole par ligne. Voici les cinq premières lignes :

© © ©

§ § § §

ª ª ª ª ª

© © © © © ©

§ § § § § § §

 Combien y aura-t-il de symboles dans la 100^e ligne ?

Démarche

La première ligne contient 3 symboles, la deuxième ligne 4 symboles, la troisième ligne 5 symboles. La différence entre le nombre de symboles et le rang de la ligne est 2.

La 100^e ligne contiendra 102 symboles.

Problème 2

Quels seront les symboles dans la 100^e ligne ?

Démarche

Chaque symbole apparaît à toutes les trois lignes. On fait : 100 ¸ 3 = 33, reste 1. Le reste correspond à la première ligne où on observe des symboles de cœur.

On aura les symboles de cœur dans la 100^e ligne.

Problème 3

En tout, combien aura-t-on écrit de symboles de trèfle si la 100^e ligne est la dernière ?

Démarche

On construit un tableau qui donne le nombre de trèfles selon le rang de chaque ligne visée.

Les trèfles apparaissent sur la deuxième ligne, la cinquième, la huitième, etc. La dernière ligne qui contient du trèfle est la 98^e de la figure, car 98 ÷ 3 = 32, reste 2. Elle contient 100 trèfles. Il s’agit d’additionner les nombres de la suite 4, 7, 10, 13, 16, …, 94, 97, 100.

On calcule le nombre de couples dont la somme est 104 (4 + 100, 7 + 97, 10 + 94, etc.). Pour cela, on fait : 100 ÷ 3 = 33, reste 1. On conserve le quotient. On compte 33 couples. La moyenne de chaque couple est 52. On fait : 33 × 52 = 1716.

On aura écrit 1716 symboles de trèfle.

Problème 4

Dans quelle ligne atteindra-t-on le 60^e trèfle ? Solution 1.07-4

* * * * * * *

1.08 Des éléphants et des gazelles

Une des propriétés des mathématiques discrètes est de s’intéresser aux entiers et de laisser de côté les nombres fractionnaires. On réfère alors à des situations de la vie courante où on ne peut pas séparer des êtres ou des objets. On peut casser un œuf, mais on ne pas avoir une fraction d’œuf. On peut compter des animaux, mais pas des fractions d’animaux.

Souvent, en mathématiques discrètes, on peut résoudre des problèmes par l’algèbre. Il arrive que des situations comprenant deux inconnues ne puissent être représentées que par une équation. Dans ce cas, il peut exister plus d’une solution. Voici un exemple :

Problème 1

Des éléphants se déplacent en groupes de 3. Des gazelles se déplacent en groupes de 2. Il y a en tout 60 bêtes.

Combien y a-t-il de groupes possibles de chaque bête ?

Démarche

Soit x le nombre de groupes d’éléphants et y le nombre de groupes de gazelles. On peut écrire : 3x + 2y = 60.

Comme 60 est un nombre pair, x devra être pair. On suppose que x = 2. Alors, y = 27. On suppose que x = 4. Alors, y = 24. On continue. Voici un tableau qui donne toutes les possibilités :

On note que les valeurs de x sont divisibles par 2 comme dans 2y et que les valeurs de y sont divisibles par 3 comme dans 3x.

Bref, il y a neuf solutions possibles, lesquelles apparaissent dans le tableau. Par exemple, on peut avoir 2 groupes d’éléphants et 27 groupes de gazelles.

Conditions. Pour s’assurer qu’il y a une seule solution, on devrait ajouter d’autres conditions. Voici des exemples :

Condition 1. En tout, le nombre de groupes est 26. Dans ce cas, il y a 8 groupes d’éléphants et 18 groupes de gazelles.

Condition 2. Le nombre de groupes d’éléphants est le même que celui de gazelles. Dans ce cas, il y a 12 groupes d’éléphants et 12 groupes de gazelles.

Condition 3. Le nombre de groupes de gazelles est six fois plus grand que celui des éléphants. Dans ce cas, il y a 4 groupes d’éléphants et 24 groupes de gazelles.

Condition 4. Le nombre de groupes d’éléphants est six fois plus grand que celui des gazelles. Dans ce cas, il y a 18 groupes d’éléphants et 3 groupes de gazelles.

Condition 5. Le nombre total de groupes est le plus grand possible. Dans ce cas, il y a 2 groupes d’éléphants et 27 groupes de gazelles.

Problème 2

Marco achète des paniers de pommes à trois pistoles le panier. Il achète aussi des paniers de pêches à cinq pistoles le panier. Le coût total est de 58 pistoles.

Combien a-t-il acheté de paniers de chaque sorte ? Solution 1.08-2

* * * * * * *  

1.09 Des poules et des veaux

Problème 1

Dans un pré, des poules picorent pendant que les veaux broutent. Un touriste compte le nombre de têtes et de pattes. Ce nombre est de 16 pour les têtes et de 52 pour les pattes.

Combien y a-t-il de poules et de veaux dans ce pré ?

Démarche 1. Écrire une équation

Soit x le nombre de poules et (16 – x) le nombre de veaux. On écrit : 2x + 4(16 – x) = 52. On résout l’équation. On trouve que x = 6 et 16 – x = 10.

On compte 6 poules et 10 veaux.

Démarche 2. Écrire deux équations

Soit x le nombre de poules et y le nombre de veaux. On écrit : x + y = 16 et 2x + 4y = 52. On résout les équations. On trouve que x = 6 et y = 10.

On compte 6 poules et 10 veaux.

Démarche 3. Procéder par raisonnement

Comme le nombre de pattes est pair autant pour les veaux que pour les poules, on peut diviser 52 par 2. Le résultat est 26. On fait : 26 – 16 = 10 : c’est le nombre de veaux. On fait : 16 – 10 = 6 : c’est le nombre de poules.

On compte 6 poules et 10 veaux.

Démarche 4. Construire un tableau

On établit un tableau dans lequel on écrit le nombre possible de poules à partir de 1. Comme il y a 16 têtes, on complète avec le nombre de veaux. On calcule le nombre de pattes.

On compte 6 poules et 10 veaux.

Problème 2

Dans un pré, des poules picorent pendant que les veaux broutent. Un touriste compte le nombre de têtes et de pattes. Ce nombre est de 39 pour les têtes et de 114 pour les pattes.

Combien y a-t-il de poules et de veaux dans ce pré ?

Démarche. Procéder par induction

Il serait fastidieux de construire un tableau jusqu’à la solution. On pose plutôt les premières hypothèses et on procède par induction par la suite.

Lorsqu’on augmente le nombre de poules de 1, le nombre de pattes diminue de 2. La différence de 154 et de 114 est 40. Comme le nombre diminue de 2, on fait : 40 ÷ 2 = 20. On fait : 38 – 20 = 18 : c’est le nombre de veaux. On fait : 39 – 18 = 21 : c’est le nombre de poules.

 Il y a 18 veaux et 21 poules.

Problème 3

Dans un pré, des poules picorent pendant que les veaux broutent. Un touriste compte le nombre de têtes et de pattes. Ce nombre est de 73 pour les têtes et de 228 pour les pattes.

Combien y a-t-il de poules et de veaux dans ce pré ? Solution 1.09-3

* * * * * * *

1.10 Veaux en couleurs

Problème 1

Tous les veaux de Bernard sont blancs, sauf 3.

Tous les veaux de Bernard sont noirs, sauf 4.

Tous les veaux de Bernard sont rouges, sauf 5.

Combien Bernard a-t-il de veaux de chaque couleur ? Combien a-t-il de veaux au total ?

Démarche 1

Soit B (blanc), N (noir) et R (rouge), on peut écrire :

N + R = 3 (première proposition)

B + R = 4 (deuxième proposition)

B + N = 5 (troisième proposition)

Posons N = 1. Alors, R = 2, B = 2, N = 3 : à rejeter car on a posé que N = 1.

Posons N = 2. Alors, R = 1, B = 3, N = 2 : valide car on a posé que N = 2.

Bernard a 2 veaux noirs, 1 rouge, 3 blancs, soit 6 veaux au total.

Démarche 2

Pour trouver le nombre de veaux, on pourrait additionner les nombres après les « sauf » et diviser par 2. Le diviseur est donné par le nombre, moins 1, de propositions. On peut écrire : 3 + 4 + 5 = 12 et 12 ÷ 2 = 6. Au total, Bernard a 6 veaux.

Pour trouver la couleur des veaux quand on connaît leur nombre, on peut procéder ainsi : du total, on soustrait le nombre de chaque « sauf » et on retient la couleur qui précède « sauf ». On fait : 6 – 3 = 3 (blancs), 6 – 4 = 2 (noirs), (6 – 5) = 1 (rouge).

Bernard a 3 veaux blancs, 2 noirs et 1 rouge.

Problème 2

Tous les veaux de Julie sont rouges, sauf 7.

Tous les veaux de Julie sont gris, sauf 8.

Tous les veaux de Julie sont noirs, sauf 6.

Tous les veaux de Julie sont blancs, sauf 9.

Combien Julie a-t-elle de veaux de chaque couleur ? Combien a-t-elle de veaux au total ?

Démarche

Inspirons-nous de la démarche précédente. Additionnons les nombres de chaque « sauf ». Cela donne 30. Divisons par 3, soit le nombre, moins 1, de propositions. Le quotient est 10. Julie a 10 veaux au total.

Trouvons la couleur des veaux. Du total, soustrayons chaque nombre de « sauf » et retenons la couleur qui précède « sauf ». On fait : 10 – 7 = 3 (rouges), 10 – 8 = 2 (gris), 10 – 6 = 4 (noirs), 10 – 9 = 1 (blanc).

Julie a 3 veaux rouges, 2 gris, 4 noirs et 1 blanc.

Si la somme des « sauf » n’est pas un multiple de 3, le problème est insoluble.

* * * * * * *

1.11 Parcours d’un lièvre

Problème 1

Dans une grille 4 × 5, un lièvre part de la case supérieure gauche en se dirigeant de gauche à droite et de haut en bas d’une case à l’autre, mais jamais en diagonale.

On veut savoir combien de chemins différents le lièvre pourra parcourir pour se rendre à la case inférieure droite.

Démarche

Voilà un problème qui demande beaucoup d’attention si on décide de tracer chacun des chemins et de les compter un à un. On risque probablement d’en oublier ou d’en compter deux fois. Par ailleurs, le temps nécessaire à ces deux opérations pourra être assez long.

Il existe un procédé simple et très efficace. Dans les cases de la première rangée horizontale, un seul chemin est possible. Il en est de même dans la première colonne. On écrit donc 1 dans les cases de ces deux rangées.

Par la suite, le nombre placé dans chaque case est la somme du nombre placé à gauche de ce nombre et de celui qui est au-dessus. Par exemple, pour trouver le nombre de la deuxième case de la deuxième rangée, on fait : 1 + 1 = 2. Cela signifie qu’il y a deux chemins qui passent par cette case. Pour trouver le nombre de la quatrième case de la troisième rangée, on fait : 6 + 4 = 10. Cela signifie qu’il y a 10 chemins qui passent par cette case. Voici le tableau complet :

Il y a 35 chemins qui permettent au lièvre de se déplacer.

Problème 2

La grille est la même, comme aussi la case de départ et celle d’arrivée, mais le lièvre ne peut pas passer par la case rouge car un piège y est caché.

Sauriez-vous trouver le nombre de chemins ? Solution 1.11-2

* * * * * * *

1.12 Une erreur de florins

Problème

Albert a 30 florins dans sa bourse. Normalement, successivement, il doit recevoir 29 florins et en donner 28, recevoir 27 florins et en donner 26, recevoir 25 florins et en donner 24, etc. Ces deux opérations doivent se succéder jusqu’à ce qu’Albert donne 10 florins. Cependant, à un moment précis, Albert a donné au lieu de recevoir. Toutefois, les opérations ont continué à se succéder dans le nouvel ordre et les montants à décroître de 1. À la dernière opération, Albert a reçu 10 florins. À la fin, il avait 32 florins.

Quel montant Albert a-t-il donné au lieu de recevoir ?

Situation normale

Ces deux tableaux illustrent la situation comme elle aurait dû se dérouler.

Démarche 1

Normalement, après la deuxième opération, Albert doit avoir 31 florins, après la quatrième 32 florins, après la sixième 33 florins. Il y a 10 doubles opérations. On fait 30 + 10 = 40. Normalement, Albert devait avoir 40 florins à la fin comme l’illustre le double tableau. En réalité, il a 32 florins au lieu de 40. La différence est 8. L’erreur a été commise à la huitième opération de la fin. Au moment où il devait recevoir 17 florins, il en a donné 17.

En effet, à la 13^e opération, soit la huitième de la fin, Albert fait successivement -17, +16, -15, +14, -13, +12, -11 et +10. Cette portion de tableau illustre la situation :

Démarche 2

Albert doit recevoir successivement 29, 27, 25, ..., 11 florins. Le nombre de termes est 10. La somme de cette suite est 10(29 + 11)/2 = 200. Albert devait donner successivement 28, 26, 24, ..., 10 florins. Le nombre de termes est 10. La somme de cette suite est 10(28 + 10)/2 = 190. On fait : 200 – 190 = 10. Comme il avait 30 florins au début, Albert devait avoir 40 florins à la fin. Il a 32 florins à la fin au lieu de 40. La différence est 8. L’erreur a été commise à la huitième opération de la fin. Au moment où il devait recevoir 17 florins, il en a donné 17.

Conclusion

Ce problème est d’une certaine complexité. Cependant, il mérite qu’on s’y arrête pour voir que finalement il n’est pas aussi rébarbatif qu’on peut se l’imaginer au départ.

* * * * * * *

1.13 La fête des Mères

La fête des Mères vise à souligner le dévouement et l’implication des mères de famille. Elle est soulignée dans plusieurs pays. Au Québec, elle a lieu le deuxième dimanche de mai. Elle arrive au plus tôt le 8 mai et au plus tard le 14 mai.

Problème 1

Connaissant le quantième de la fête des Mères en une année, comment trouver le quantième de l’année suivante ?

Démarche

• Quand l’année cherchée est ordinaire, on soustrait 1 au quantième donné.

• Quand l’année cherchée est bissextile, on soustrait 2 au quantième donné.

• Si le résultat est plus petit que 8, on additionne 7.

• Si le résultat est plus grand ou égal à 8, c’est le quantième cherché

En 1999, cette fête a eu lieu le 9 mai. Quel a été le quantième en 2000 ? On fait : 9 – 2 = 7 et 7 + 7 = 14. En 2000, la fête a eu lieu le 14 mai.

En 2017, cette fête a lieu le 14 mai. Quel sera le quantième en 2018 ? On fait : 14 – 1 = 13. En 2018, la fête a eu lieu le 13 mai.

Problème 2

Connaissant le jour de la semaine du 1^er janvier d’une année, comment trouver le quantième de la fête des Mères en cette même année ?

Démarche

• Quand l’année est ordinaire, le 1^er mai sera le jour de la semaine suivant celui du 1^er janvier.

• Quand l’année est bissextile, le 1^er mai sera le deuxième jour de la semaine suivant celui du 1^er janvier.

• On identifie le quantième du premier dimanche après le 1^er mai, puis du second dimanche.

En 2018, le 1^er janvier a été un lundi. Le 1^er mai a été un mardi. Le premier dimanche a été le 6 et le second le 13. En 2018, la fête a été célébrée le 13 mai.

En 2020, le 1^er janvier a été un mercredi. Le 1^er mai a été un vendredi. Le premier dimanche a été le 3 et le second le 10. En 2020, la fête a été célébrée le 10 mai.

Problème 3

Pour une année donnée du 21^e siècle, comment trouver le quantième de la fête des Mères ?

Démarche

• On prend les deux derniers chiffres de l’année.

• On divise ce nombre par 4 et on retient le quotient en ignorant le reste.

• On additionne les deux derniers chiffres de l’année et le quotient.

• On divise la somme par 7 et on conserve seulement le reste.

• On soustrait le reste de 14.

Quel sera le quantième en 2025 ? On 25 ÷ 4 = 6, reste 1. On retient 6. On fait : 25 + 6 = 31. On fait : 31 ÷ 7 = 4, reste 3 et 14 – 3 = 11. En 2025, la fête aura lieu le 11 mai, tout comme, par exemple, en 2014, 2031, 2042 et 2053.

Problème 4

En 2013, la fête des Mères a été célébrée le 12 mai. 

À quelle date, cette fête a-t-elle été célébrée en 2015 ? Solution 1.13-4

* * * * * * *

1.14 La fête des Pères

La fête des Pères a été célébrée pour la première fois en 1910 aux États-Unis. La date de cette fête varie selon les pays. Au Québec, cette fête arrive le troisième dimanche de juin, soit du 15 au 21.

Problème 1

Trouver le quantième de cette fête pour une année donnée du 21^e siècle.

Démarche

• On prend les deux derniers chiffres de l’année.

• On divise ce nombre par 4 et on retient le quotient en ignorant le reste.

• On additionne les deux premiers résultats.

• On divise la somme par 7 et on conserve seulement le reste.

Le tableau suivant indique le quantième pour chaque reste.

Par exemple, quel sera le quantième en 2025 ? On prend 25. On divise par 4. Le résultat est 6, reste 1. On retient 6. On fait : 25 + 6 = 31. On divise 31 par 7. Le résultat est 4, reste 3. On va dans le tableau. Le reste 3 correspond au quantième 15. En 2025, la fête des Pères aura lieu le 15 juin, tout comme, par exemple, en 2014, 2031, 2042 et 2053.

Problème 2

En 2021, la fête des Pères a été célébrée le 20 juin. 

À quelle date, cette fête a-t-elle été célébrée en 2023 ? Solution 1.14-2

Commentaires

L’algorithme donné est de peu d’intérêt pratique. Mais, le fait de pouvoir trouver le quantième à travers cet outil montre une application de plus pour les mathématiques. C’est d’ailleurs dans une telle démarche que les mathématiques récréatives puisent leurs lettres de noblesse.

Si on veut passer pour un petit futé, on demande à une autre personne d’énoncer une année du 21^e siècle. Après avoir mémorisé le tableau et fait mentalement les calculs appropriés, on énonce le quantième de la fête des Pères.

* * * * * * *