La figure est formée de 17 allumettes et compte six carrés.

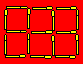
Enlevez trois allumettes pour obtenir quatre carrés.

Émilien dispose ses 135 chevaux dans cinq enclos. Il doit toujours y avoir un cheval de plus dans tout enclos de droite.

Déterminez le nombre de chevaux pour chacun des cinq enclos.

Écrivez des nombres de 1 à 5 dans cette grille. Les nombres doivent être différents sur chaque ligne, dans chaque colonne et dans chaque diagonale.

Dans ce tableau, chacune des lettres A, B, C, D et E correspond à un chiffre différent. La somme des nombres de chaque ligne est donnée à droite et celle de chaque colonne en bas. Quand deux lettres sont accolées, elles forment un nombre de deux chiffres.

Quelle est la valeur de E ?

Dans les cercles, écrivez deux 2, trois 3 et un 5. Le résultat doit être 4.

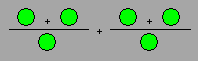
Dans cette addition, il manque deux nombres. L’un est le double de l’autre.

Trouvez ces deux nombres.

Dans une grille 5 ´ 5, Julie veut placer les nombres de 1 à 25. La somme doit être la même sur chaque ligne et dans chaque colonne.

Quelle est cette somme ?

En partant de la case numéro 1, déplacez le cavalier. Il doit passer une seule fois dans chaque case jusqu’à ce qu’il ait atteint toutes les cases. Les cinq premiers sauts sont indiqués.

Numérotez au passage chaque case jusqu’à 25.

Philibert part de Gville pour se rendre à Dville en traversant quatre villes différentes.

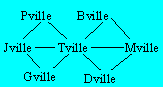
Indiquez un chemin qui ne passe pas par Bville.

Dans l’addition suivante, remplacez trois chiffres par 1 de manière à ce que la somme soit 602.

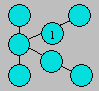
Dans les cercles, écrivez des nombres de 2 à 12. Le produit des nombres des cercles reliés par une  droite doit être égal à 84.

Martin part de Kville pour se rendre à Gville. Dans une ville marquée A, il livre 25 automobiles, dans B 22 automobiles, dans C 18 automobiles, dans D 10 automobiles. Il traverse exactement quatre villes.

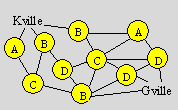
Quel est le chemin qui permet de livrer le plus d’automobiles ?

Dans la grille, écrivez des nombres de 10 à 100. On doit retrouver des chiffres différents sur chaque ligne, dans chaque colonne et dans chaque diagonale.

Quatre nombres et quatre opérations sont donnés.

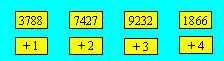
Faites sur chacun des nombres une des quatre opérations. Vous devez obtenir quatre nombres qui sont lus horizontalement et verticalement.

Complétez la grille.

Pierre a placé huit lapins dans chacun des neuf enclos communicants. Un peu plus tard, l’enclos B est vide et l’enclos C contient 11 lapins. Pourtant, il y a toujours 24 lapins dans chaque rangée horizontale, verticale et diagonale.

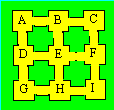
Indiquez le nombre de lapins dans les autres enclos à ce moment-là.

Dans la multiplication, trouvez les chiffres qui manquent.

Dans cette figure, Martine veut placer chacun des nombres de 3 à 7. Elle a d’abord inscrit le 8, le 9 et le 10.

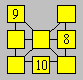
Écrivez les autres nombres pour que la somme des nombres des cases reliées par une droite soit égale à 18.

Dans cette addition, Maténix s’est amusé à remplacer chaque lettre par un chiffre différent. Par exemple, S = 2, A = 4 et T = 3.

À quel nombre correspond MATH ?

2⁹⁹ + 3⁹⁹ est-il divisible par 3 ?

Chaque symbole représente un chiffre différent. La somme de chaque ligne est donnée à droite et celle de chaque colonne en bas. Quand deux symboles sont accolés, ils forment un nombre de deux chiffres.

Quelle est la valeur de ( ?

Dans l’addition suivante, remplacez deux chiffres par 2 de manière à ce que la somme soit 909.

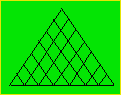
Dans cette figure, combien peut-on compter de losanges formés de quatre parties ?

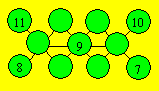
Dans les cercles, écrivez chacun des nombres de 1 à 6. La somme des nombres de trois cercles reliés par une droite doit être 16.

Vous prenez le nombre 40. Vous faites ces opérations dans différents ordres : additionner 5, soustraire 5, multiplier par 5 et diviser par 5.

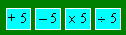
Trouvez le plus grand résultat.

Dans les cercles, écrivez 1, 2, 3, 4, 5 et 6. Le résultat doit être 2.

Dans le tableau, chaque lettre correspond à un des chiffres donnés sur la même ligne. Par exemple, J est égal à 1, 8 ou 9.

Trouvez le mot qui correspond à 518 008.

Marc désire placer ses 63 chevaux dans neuf enclos. Les enclos des coins contiennent 3, 6, 8 et 11 chevaux. Le nombre de chevaux doit être le même dans chaque rangée horizontale, verticale et diagonale.

Déterminez le nombre de chevaux dans chacun des cinq enclos vides.

Jean choisit un nombre de deux chiffres. Il additionne les deux chiffres : c’est la valeur de A. Il additionne le nombre et son renversé. Il divise le résultat par 11 : c’est la valeur de B. 

Quelle est la valeur de B - A ?

En utilisant chacun des chiffres ci-dessous, formez quatre nombres de quatre chiffres qui sont divisibles par 8.

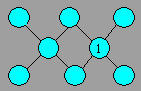
Dans les cercles, écrivez deux 3, deux 6 et deux 7. Le résultat doit être 2.

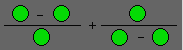
Dans les cercles, écrivez des nombres de 2 à 15. Le produit des nombres des cercles reliés par une  droite doit être égal à 90.

Dans cette addition, il manque deux nombres. L’un est le carré de l’autre.

Trouvez ces deux nombres.

Dans cette série de six dominos, la rangée supérieure contient 20 points et la rangée inférieure 12 points.

Bougez deux dominos afin d’obtenir 16 points dans chacune des deux rangées.

ABCD est un nombre de quatre chiffres différents. On peut écrire :

Quelle est la valeur de ABCD lorsque C = 3 ?

Dans ce premier tableau, chaque lettre de l’alphabet est associée à un chiffre.

Ce second tableau contient une phrase.

Déchiffrez cette phrase.

Dans cette grille, écrivez des nombres de 1 à 7. Les nombres doivent être différents sur chaque ligne et dans chaque colonne.

Dites à un ami de choisir une date, de multiplier le quantième par 12 et le rang du mois par 31, d’additionner les deux produits et de vous transmettre la somme. Pour le 6 juillet, on fait : (6 ´ 12) + (7 ´ 31) = 289. 

Quel est le mois lorsque la somme est 141 ?

Écrivez chacun des nombres de 1 à 7 sauf 2 pour que la somme soit 14 dans chaque rangée de trois cercles.

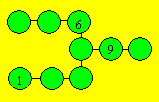
Dans les cases, placez chacun des chiffres de 1 à 5. L’un des nombres est un multiple de 5.

Trouvez trois nombres dont la somme est 51.

Cette grille doit contenir cinq nombres de cinq chiffres qui sont lus horizontalement et verticalement. 

A : 19 106 ´ par 2, 4 ou 6                 B : 9 979 ´ par 3, 5 ou 7
C : 6 096 ´ par 6, 8 ou 10                 D : 3 662 ´ par 5, 7 ou 9
E : 3 373 ´ par 3, 13 ou 33

En choisissant les bons produits, complétez la grille.

Un fermier plus fantaisiste que mathématicien s’est construit une passerelle sur une petite rivière. La passerelle peut supporter un poids de 72 kilos. Le fermier pèse 71 kilos. Il doit traverser la rivière avec trois boules de 0,5 kilo chacune. 

Comment s’y prendra-t-il ?

Combien de nombres divisibles par 2 peuvent être formés avec ces quatre chiffres ?

Dans chacun des huit enclos d’une bergerie, on trouve six moutons. À un moment donné, huit moutons se sauvent. Le préposé à la bergerie modifie le nombre de moutons par enclos de façon à avoir encore 18 moutons sur chacun des quatre côtés.

Effectuez la nouvelle disposition.

Trouvez deux nombres dont la différence des carrés est 224.

Dans les cercles, écrivez des nombres de 2 à 15. Le produit des nombres des cercles reliés par une  droite doit être égal à 120.

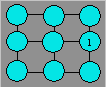
En partant de la case numéro 1, déplacez le cavalier. Il doit passer une seule fois dans chaque case jusqu’à ce qu’il ait atteint toutes les cases. Les 10 premiers sauts sont indiqués.

Numérotez chaque case jusqu’à 36.

Des objets dont le poids est exprimé en nombres entiers sont placés sur les plateaux d’une balance en équilibre. Le cercle noir pèse 10 grammes.

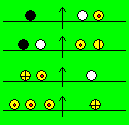
Quel est le poids de chacun des quatre autres objets ?

Dans un magasin de sept rayons, il y a 62 employés. À un moment donné, il y a huit employés dans le rayon inférieur gauche et 26 employés dans chacune des six rangées de trois rayons.

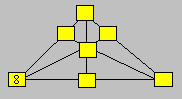
Déterminez le nombre d’employés par rayon.

Chaque lettre représente un chiffre différent. Quand deux lettres sont accolées, elles forment un nombre de deux chiffres.

À quel nombre correspond FADE ?

En utilisant cinq 4, représentez successivement 1, 2, 3, 4, 5 et 6. Les opérations permises sont : +, –, ´ et ¸.