Ceci est le premier livre édité par Récréomath.

Amusements 
mathématiques

Par Charles-É. Jean

Cette édition comprend 200 problèmes et leur solution. Une version anglaise a été éditée.

Solutions 1 à 50

Solutions 101 à 150

***************
Solutions 51 à 100
***************

Solution 51. Voici une répartition des poules :

Solution 52. La dernière rangée de fleurs doit couper les rangées déjà existantes. Pour quatre rangées, on aura 7 + 4 = 11 arbres.

Solution 53. Voici trois carrés :

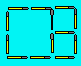
Solution 54. E = 19, G = 17, C = 21 et I = 29. La somme des nombres dans chaque rangée est 57. Le tableau rempli est :

Solution 55. Il y a trois chemins possibles.

Tville, Bville, Mville
Pville, Tville, Mville
Gville, Tville, Mville.

Solution 56. On remplace le 3 et le 7 de la colonne des unités ; puis le 2 et le 8 de la colonne des dizaines.

Solution 57. On peut compter 30 carrés.

Solution 58. On peut écrire : 4 + 56 – 12 – 34 = 14.

Solution 59. Les nombres divisibles par 7, 11, 12 et 13 sont respectivement 8568, 6226, 5172 et 5577. On assemble les chiffres 5, 2, 2 et 7. Le carré est 7225.

Solution 60. La différence est 3.

Solution 61. Les nombres sont : 327, 654 et 981.

Solution 62. Justin a travaillé six jours. En effet, après cinq jours il avait réalisé la moitié du casse-tête.

Solution 63. On peut écrire : 123 + 45 – 67 – 89 = 12.

Solution 64. Le résultat est toujours le plus grand nombre.

Solution 65. Un chemin est :

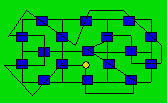
Solution 66. On peut avoir trois rectangles de mesures différentes : 5 ´ 18, 6 ´ 15 et 9 ´ 10.

Solution 67. Voici une façon de représenter chacun des nombres de 1 à 8 :

Solution 68. Comme il y a 25 cases, chaque partie contient cinq cases. Le partage se fait ainsi :

Solution 69. Voici une façon de représenter chacun des nombres de 1 à 6 :

D'autres exemples sont donnés pour 1 :

Solution 70. D = 1, N = 2, S = 3, A = 4, B = 5, R = 6, V = 7, E = 8 et L = 9. L’inscription est : BALLES À VENDRE.

Solution 71. Voici une façon de représenter chacun des nombres de 7 à 12 :

Solution 72. On compte 24 carrés 3 ´ 3.

Solution 73. On suppose que le plus petit poids est d’un gramme, le deuxième sera de deux grammes, le troisième de quatre grammes et le quatrième de huit grammes. Au total, on pourrait peser un objet de 15 grammes. Chacun des poids doit être quatre fois plus pesant. Les poids utilisés sont de 4, 8, 16 et 32 grammes.

Solution 74. Les combinaisons de deux nombres dont la somme est 16 sont : (6, 10) et (7, 9). Les combinaisons de trois nombres dont la somme est 16 sont : (1, 5, 10), (1, 6, 9), (1, 7, 8), (2, 4, 10), (2, 5, 9), (2, 6, 8), (4, 5, 7) et (4, 6, 6). Une disposition des nombres est :

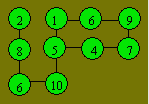
Solution 75. Le plus grand nombre est 2⁶ = 64.

Solution 76. Une figure est :

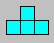
Solution 77.  La disposition des clous est :

Solution 78. Les chiffres 1, 4, 2, 8, 5 et 7 se suivent de façon circulaire. Le dernier chiffre est 5. Le produit est 714 285.

Solution 79. Un nombre est divisible par 4 quand le nombre formé par les deux derniers chiffres est divisible par 4. Les deux derniers chiffres possibles sont : 24, 32 et 52. On peut former six nombres : 3452, 3524, 4352, 4532, 5324 et 5432.

Solution 80. Il y a deux façons. Dans l’ordre, les opérations sont : (´, +, ¸, -, Ö ) ou (-, ´, +, ¸ et Ö ).

Solution 81. La somme totale des nombres est 189. La somme par rangée est 63. Voici une façon de répartir les nombres :

Solution 82. L’égalité est : 2² + 4² + 5² = 3² + 6².

Solution 83. Il y a 12 chemins possibles.

Solution 84. On fait 99 964 + 99 963 = 199 927. La différence des deux carrés est 199 927.

Solution 85. Les fleurs peuvent être disposées ainsi :

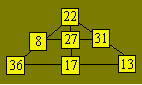
Solution 86. Ce nombre est 72. Il est divisible par 2, 3, 4, 6, 8 et 9.

Solution 87. La plus grande expression est 3⁴.

Solution 88. Robert a acheté 15 timbres de huit centimes et quatre timbres de sept centimes.

Solution 89. Dans cinq ans, René aura 14 ans et sa mère 42 ans.

Solution 90. Albert devra placer 51 écus par rangée. Le montant par case est :

Solution 91. On peut compter cinq triangles.

Solution 92. A = 9, car N = 3 et A + A + N = 21. La valeur de MAP est 195.

Solution 93. La somme totale des numéros est 39. Les plus petits éléments des sommets doivent être 4, 5 et 6, puis ceux des centres 7, 8 et 9. La plus petite somme est 18.

Solution 94. Le quantième est 21.

Solution 95. Une égalité est : 18 + 25 + 34 + 67 = 144.

Solution 96. Ce nombre est 104.

Solution 97. Lorsqu’on soustrait 1 au numéro, le résultat est divisible par 14. Les multiples de 14 sont : 14, 28, 42, 56, 70, 84 et 98. Quand on additionne 1, on obtient : 15, 29, 43, 57, 71, 85 et 99. Le numéro civique  est 57.

Solution 98. On trace la droite sur 7, 2 et 9.

Solution 99. Selon la puissance du nombre, on note le dernier chiffre dans ce tableau.

Le dernier chiffre est 1 pour les puissances 4, 8, 12… Le dernier chiffre de 247¹⁰⁰ est 1.

Solution 100. Le carré rempli est :

Solutions 1 à 50

Solutions 101 à 150