Quel est le numéro de téléphone du club ?

Neuf autobus transportent 234 passagers. À un moment donné, les neuf autobus comptent un même nombre de passagers dans chaque rangée horizontale, verticale et diagonale. De plus, les autobus B et G transportent respectivement 39 et 31 passagers.

Quel est le nombre de passagers des autres autobus ?

Des deux expressions, laquelle est la plus grande : 8⁹ ou 9⁸ ?

Vous prenez le nombre 40. Vous faites ces opérations dans différents ordres : additionner 5, soustraire 5, multiplier par 5 et diviser par 5.

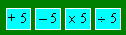
Trouvez le plus petit résultat.

Dans le tableau suivant, chacune des lettres correspond à un chiffre différent. Par exemple, M = 3 et G = 7. La somme de chaque ligne est donnée à droite et celle de chaque colonne en bas. Quand deux lettres sont accolées, elles forment un nombre de deux chiffres.

Quelle est la valeur de JP ?

Sur le tableau, un pion part du point A. Il se déplace en diagonale et s’arrête sur la dernière rangée horizontale.

Combien y a-t-il de chemins possibles ?

Maténix a décidé d’écrire les chiffres au moyen de boules.

Quel est le plus grand nombre impair de deux chiffres différents qui exige 10 boules ?

Dans cette figure, Martin veut placer chacun des nombres de 3 à 11. Il a d’abord inscrit le 5 et le 8.

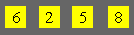
Écrivez les autres nombres pour que la somme des nombres des cases reliées par une droite soit 21.

Examinez attentivement les nombres placés dans les trois premiers cercles.

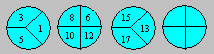
Complétez le quatrième cercle.

Un magasin de vêtements a payé cet espace publicitaire dans un journal. Le coût de trois articles est mentionné.

Trouvez le coût des autres articles, étant donné que le coût total est de 108 euros dans chaque rangée horizontale, verticale et diagonale.

Placez des signes + entre certains chiffres de ce nombre de façon à ce que la somme soit 121.

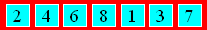
Représentez 100 en utilisant successivement six 8, sept 8, huit 8, neuf 8, dix 8 et onze 8. Les opérations permises sont : +, –, ´ et ¸.

Raymond a partagé son champ en 30 parcelles carrées. Il a planté six arbres, un par parcelle.

Combien peut-on compter de terrains 2 ´ 2 qui contiennent un seul arbre ?

Gérard a un sac de billes. Il vend le tiers de son sac et donne trois billes. À nouveau, il vend le tiers de ce qui lui reste et donne trois billes. Une dernière fois, il vend le tiers de ce qui lui reste et donne trois billes. Il lui reste alors sept billes dans son sac. Combien Gérard possédait-il de billes ?

Complétez la grille de manière à ce que la somme des nombres de chaque ligne et de chaque colonne soit 50.

Maténix a décidé d’écrire les chiffres au moyen de boules.

Trouvez le plus petit nombre pair de deux chiffres qui exige 11 boules.

Henri choisit un nombre de deux chiffres. Il le multiplie par 3, y additionne 12, divise par 3 et soustrait le nombre choisi. Quel est le résultat par rapport au nombre choisi ?

Trouvez le 15^e terme de cette suite : 2, 5, 4, 7, 6, 9, 8, 11, ...

Martin a acheté 99 fleurs. Il veut les répartir en six îlots. Il plante d’abord dans chaque sommet 10, 12 et 17 fleurs. Le nombre de fleurs doit être le même dans chaque rangée de trois îlots.

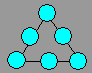
Combien Martin devra-t-il placer de fleurs dans chacun des îlots des centres ?

La figure est formée de 17 allumettes et compte six carrés.

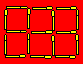
Enlevez six allumettes pour obtenir deux rectangles.

Trouvez deux nombres dont la somme des carrés est 274.

Emmanuelle veut réaliser un tapis carré formé de 25 carreaux de même grandeur. Elle a cinq carreaux rouges, cinq bleus, cinq jaunes, cinq violets et cinq gris. Huit carreaux ont déjà leur couleur.

Agencez les couleurs pour qu’une seule apparaisse dans chaque rangée horizontale, verticale et diagonale.

En passant par les points de cette figure, construisez six losanges de même grandeur.

Dans une boîte, Anne place 15 jetons. 

· cinq jetons marqués 1 point

· cinq jetons marqués 2 points

· cinq jetons marqués 5 points

Rémi désire neuf jetons dont les marques totalisent 17 points. Quels jetons Rémi recevra-t-il ?

Anthime possède quatre immeubles à logements. Le numéro de chacun d’entre eux est composé des mêmes quatre chiffres dont la somme est 20. La somme des quatre numéros est 22 220.

Quels sont les numéros ?

Quatre fois la somme de deux chiffres d’un nombre est égal à ce nombre. Le double du produit des deux chiffres est aussi égal à ce nombre. 

Quel est ce nombre ?

Dans l’addition, chaque lettre est mise pour un chiffre différent. Par exemple, E = 2 et M = 8.

Quelle est la valeur de FORCE ?

Pascal trace un trait continu d’un point de la circonférence à un autre. Il partage ainsi le cercle en cinq parties.

Tracez deux autres droites de façon continue pour avoir un maximum de parties. Quel est ce nombre ?

Parmi les six nombres, il en existe un seul qui n’est pas un carré.

Trouvez ce nombre sans extraire de racine carrée.

Cette figure est composée de huit boules et présente cinq rangées de trois boules chacune.

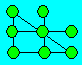
En utilisant sept boules, formez quatre rangées de trois boules chacune.

Chaque lettre représente un chiffre différent. Par exemple, R = 8.

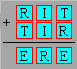
À quel nombre correspond RITE ?

Les diviseurs de 16 sont 1, 2, 4, 8 et 16. La somme de ces diviseurs est 31. Trouvez un autre nombre dont la somme des diviseurs est 31.

Dans les quatre opérations, chaque lettre représente un chiffre différent.

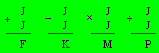
Quelle est la valeur de FKMP ?

Dans un village, on a adopté un nouveau système de nombres dans lequel il n’y a que deux chiffres, 0 et 1. Voici la table d’équivalence :

Il y a 11 ´ 111 ´ 1111 habitants dans ce village. Quel est ce nombre dans notre système ?

Dans cette série de six dominos, la rangée supérieure contient 20 points et la rangée inférieure 12 points.

Bougez deux dominos afin d’obtenir le même nombre de points dans chacune des deux rangées.