*****************
Solutions 151 à 200
*****************
Solution 151. Voici trois carrés :

Solution 152. On peut compter six carrés.
Solution 153. On peut avoir : (1, 2, 5, 8), (1, 2, 6,
7), (1, 3, 4, 8), (1, 3, 5, 7), (1, 4, 5, 6), (2, 3, 4, 7), (2, 3, 5, 6). Il y a
sept groupes de quatre jetons dont la somme est 16.
Solution 154. A = 7 et B = 12.
Solution 155. Si on divise chaque nombre de la suite par 4,
le reste est 3. Par ailleurs, quand on divise un carré par 4, le reste est 1.
On ne compte aucun carré dans cette suite.
Solution 156. L’expression est : 6 ÷ 2 × 5 - 8.
Solution 157. Il y a deux rectangles dont la somme est moins
de 26 : un horizontalement (3, 8, 2, 4, 3) et un verticalement (2, 4, 7, 4, 3,
5).
Solution 158. Comme on effectue une division, il faut que les
nombres choisis soient des diviseurs de 77. Les nombres possibles sont : 7,
11 et 77. Le plus petit nombre est 7.
Solution 159. On peut intervertir le 3 et le 4, le 6 et le 9,
le 10 et le 13, le 15 et le 16.
Solution 160. On enlève deux segments du 4 pour donner 1 et
on déplace un segment vertical du 3 pour donner 2. Le plus petit nombre est 12.
Solution 161. Une égalité est : 17 + 25 + 34 + 68 =
144.
Solution 162. On compte six carrés 3 ´
3.
Solution 163. La grille remplie est :
|
4 |
6 |
5 |
2 |
1 |
3 |
|
1 |
3 |
4 |
6 |
5 |
2 |
|
5 |
2 |
1 |
3 |
4 |
6 |
|
3 |
4 |
6 |
5 |
2 |
1 |
|
6 |
5 |
2 |
1 |
3 |
4 |
|
2 |
1 |
3 |
4 |
6 |
5 |
Solution 164. Lyne est née un dimanche.
Solution 165. On compte neuf carrés 3 ´
3.
Solution 166. Le nombre choisi est 36.
Solution 167. Une égalité est : 4 × 4 + 4 = 5 × 5 -
5.
Solution 168. Il y a trois ans de différence. Pierre a eu le
double de l’âge de Marie il y a 26 ans. Pierre avait alors six ans et Marie
trois ans.
Solution 169. Roméo achètera 18 timbres de chaque valeur.
Solution 170. Voici une configuration :
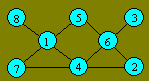
Solution 171. Jeanne a 14 ans.
Solution 172. Les unités sont 4, 5 et 6. Les dizaines sont
1, 2 et 3. La plus petite somme est 75.
Solution 173. On peut compter 12 carrés 3 ´
3.
Solution 174. Il n’y a pas eu de 29 février en 2001, car l’an
n’est pas bissextile.
Solution 175. Ce nombre est 24.
Solution 176. On additionne 2 une première et une deuxième
fois ; puis on soustrait 1. On répète ces opérations. Les termes de
rangs 1, 4, 7, 10 sont égaux à leur rang. Le terme de rang 19 est 19.
Solution 177. On compte 25 carrés 4 ´
4.
Solution 178. Une figure est :

Solution 179. Une brique pèse trois kilogrammes. Quatre
briques pèsent 12 kilogrammes.
Solution 180. L’égalité est : 392 + 475 = 867.
Solution 181. On compte 10 carrés : 9, 36, 81, 144,
225, 324, 441, 576, 729 et 900.
Solution 182. Jamais, car parvenu au 81e étage,
Mario ne pourra pas monter de cinq étages.
Solution 183. Réal a vécu 61 jours.
Solution 184. Une disposition des nombres est :
|
2 |
´ |
3 |
= |
6 |
|
9 |
– |
5 |
= |
4 |
|
1 |
+ |
7 |
= |
8 |
Solution 185. Une disposition des nombres est :
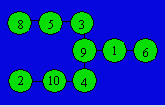
Solution 186. Les opérations sont dans l’ordre : -,
¸, Ö, ´
et +.
Solution 187. L’égalité est : 246 + 813 + 7 = 1 066.
Solution 188. Deux carrés ont une somme de plus de 21 :
(5, 7, 3 et 9) et (9, 2, 5 et 7).
Solution 189. Martin possédait 39 billes.
Solution 190. Le résultat est le double du nombre choisi.
Solution 191. On additionne les deux premiers nombres, ce qui
donne le troisième nombre. On soustrait 1 au troisième nombre et on répète
ces opérations. Le terme de rang 14 est 192.
Solution 192. Lorraine recevra un jeton marqué 1, trois
jetons marqués 2 et deux jetons marqués 5.
Solution 193. Une figure est :

Solution 194. Non. Par exemple, on prend 7 et 9 : 7 × 9
= 63 et 8 × 8 = 64. On prend 11 et 13 : 11 × 13 = 143 et 12 × 12 = 144.
Le carré est supérieur d’une unité à l’autre produit.
Solution 195. Une disposition des boules est :
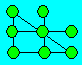
Solution 196. S = 9, B = 7 et R = 5.
Solution 197. On enlève les trois segments horizontaux du 8.
Cela donne 11. Le plus grand nombre est 115.
Solution 198. Une expression est : (7 ´
100) – (8 ´ 75) + 9.
Solution 199. Une figure est :

Solution 200. La dernière pièce est celle qui est au rang 5
par rapport au départ.
|
![]()
![]()