Ceci est le premier livre édité par Récréomath.

Amusements 
mathématiques

Par Charles-É. Jean

Cette édition comprend 200 problèmes et leur solution. Une version anglaise a été éditée.

Solutions 1 à 50

Solutions 51 à 100

Solutions 101 à 150

*****************
Problèmes 51 à 100
*****************

Dans un poulailler où on trouve 12 poules blanches, 12 noires et 12 grises, il y a 36 perchoirs. À un moment donné, 12 poules sont dans les positions indiquées.

Disposez les 24 autres poules pour qu’il y ait deux poules de même couleur dans chaque rangée horizontale, verticale et diagonale.

Dans un terrain circulaire, un paysagiste doit placer des rangées de fleurs en ligne droite et planter un arbre dans chaque partie vide. Voici comment le paysagiste a disposé les trois premières rangées de fleurs :

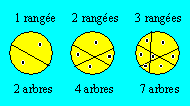
Combien d’arbres au maximum le paysagiste pourra-t-il planter s’il ajoute une autre rangée ?

La figure est formée de 17 allumettes et compte six carrés.

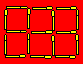
Enlevez quatre allumettes pour obtenir trois carrés.

D'après les indices donnés, remplissez la grille de façon à ce que la somme des nombres sur chaque ligne, dans chaque colonne et dans chaque diagonale soit la même.

Partant de Jville, Philibert désire se rendre à Dville en traversant trois villes.

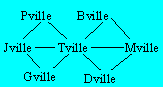
Combien y a-t-il de chemins possibles ?

Dans cette addition, remplacez quatre chiffres par 5 de manière à ce que la somme demeure 974.

Combien peut-on compter de carrés de toute grandeur dans cette grille 4 × 4 ?

Placez des signes + ou - entre certains chiffres de ce nombre de façon à obtenir 14 comme résultat.

Complétez les quatre premiers nombres. Le cinquième nombre est formé des chiffres manquants.

Trouvez le carré.

Marie choisit un nombre. Elle fait les opérations dans cet ordre : multiplier par 4, additionner 4, diviser par 4 et soustraire 4.

Quelle est la différence entre le nombre choisi et le résultat ?

Trouvez trois nombres de trois chiffres.

Ils sont formés par chacun des chiffres de 1 à 9.

Le deuxième nombre est le double du premier.

Le troisième est le triple du premier.

Le dernier chiffre du troisième nombre est 1.

Justin a entrepris de monter un casse-tête. À chaque jour, il double le nombre de pièces. Au bout de cinq jours, il a placé la moitié de ses morceaux. Trouvez le nombre de jours pendant lesquels Justin aura travaillé à la réalisation de son casse-tête.

Placez des signes + ou – entre certains chiffres de ce nombre. Le résultat doit être 12.

Dérek choisit trois nombres inférieurs à 100.
Il soustrait le moyen du plus grand.
Il soustrait le plus petit du moyen.
Il additionne les deux résultats précédents.
Il additionne le plus petit nombre.

Quel résultat Dérek obtiendra-t-il ?

L’immeuble ci-dessous possède 17 portes.

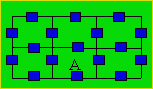
En partant du point A, vous devez franchir toutes les portes une seule fois et revenir au point de départ. Tracez un chemin.

Renaud achète 90 tuiles d’un mètre de côté et les dispose en un rectangle dont tout côté mesure plus de trois mètres. Combien y a-t-il de rectangles ayant des mesures différentes en valeurs entières ?

En utilisant chacun des chiffres ci-dessous une seule fois, représentez successivement 1, 2, 3, 4, 5, 6, 7 et 8. Les opérations permises sont : +, –, ´ et ¸, de même que la racine carrée.

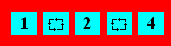
Partagez la grille en cinq parties de même grandeur mais pas nécessairement de même forme. Il doit y avoir un A et un B dans chaque partie.

En utilisant quatre 3, représentez successivement 1, 2, 3, 4, 5 et 6. Les opérations permises sont : +, –, ´ et ¸.

Un panneau publicitaire contient l’inscription ci-après. Chaque chiffre correspond à une lettre.

E + V = DB               N + D = S              S + S = R                 N + R = E
L – V = N                 B – A = D              N + N + N + N = E

Déchiffrez l’inscription.

En utilisant cinq 4, représentez successivement 7, 8, 9, 10, 11 et 12. Les opérations permises sont : +, –, ´ et ¸, de même que la racine carrée.

Combien peut-on compter de carrés 3 ´ 3 dans une grille 6 ´ 8 ?

Un épicier désire peser un objet de 60 grammes au moyen d’une balance à plateaux. Il utilise quatre poids différents tels que chacun est deux fois plus pesant qu’un autre. Quels sont les poids utilisés par l’épicier ?

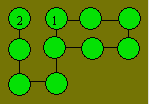
Dans les cercles, écrivez chacun des nombres de 4 à 10. Un 6 apparaît une deuxième fois. La somme des nombres de deux ou trois cercles reliés par une droite doit être égale à 16.

Quel est le plus grand nombre qu’on peut écrire avec un 2 et un 6 ?

Formez quatre carrés de même grandeur en utilisant sept droites.

Sur un mur en briques, Albert plante des clous décoratifs. Sur chaque brique, le nombre de clous est égal à la quantité de clous qui se trouvent sur les deux briques inférieures. Albert avait inscrit le nombre de clous par briques, mais quelqu’un a effacé neuf nombres.

Indiquez le nombre de clous sur les briques non marquées.

142 857 est un nombre curieux. En effet, 142 857 ´ 2 = 285 714, 142 857 ´ 3 = 428 571 et 142 857 ´ 4 = 571 428. Sans faire de calculs au long, trouvez le produit de 142 857 et de 5.

Combien de nombres divisibles par 4 peuvent être formés avec ces quatre chiffres ?

Vous prenez 28. Vous faites ces opérations dans différents ordres : additionner 4, soustraire 4, multiplier par 4, diviser par 4 et extraire la racine carrée. Le résultat est 5. 

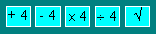
Indiquez l’ordre des opérations.

Armand a découpé une partie d’un calendrier comme ci-dessous. Il désire déplacer les quantièmes de façon à obtenir la même somme dans chaque rangée horizontale, verticale et diagonale. Le 21 demeure en place. Le 14 et le 20 sont chacun dans un coin.

Trouvez une disposition.

Trouvez une égalité de la forme A² + B² + C² = D² + E². Les valeurs des lettres sont 2, 3, 4, 5 et 6.

Sur le tableau, un pion part du point A. Il se déplace en diagonale et s’arrête sur la dernière rangée horizontale.

Combien y a-t-il de chemins possibles ?

Calculez la différence entre le carré de 99 964 et le carré de 99 963.

Un jardinier a acheté 154 plants de fleurs. Il doit disposer ses fleurs dans sept îlots répartis comme suit. Trois des sept îlots doivent contenir chacun 8, 27 et 31 fleurs. L’îlot supérieur en contient 22. Le nombre de fleurs est de 66 dans chaque rangée de trois îlots.

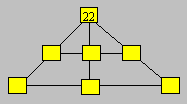
Déterminez le nombre de fleurs par îlot.

Quel est le nombre inférieur à 100 qui peut être divisé par la plus grande quantité de nombres de 2 à 9 ?

Des quatre expressions, laquelle est la plus grande : 2⁵, 3⁴, 4³ ou 5² ?

Robert désire acheter des timbres pour un montant de 148 centimes. Il veut le plus grand nombre de timbres de huit centimes et pour le reste des timbres de sept centimes. Combien de timbres de sept et de huit centimes recevra-t-il  ?

René a neuf ans. Sa mère a 37 ans. Dans combien d’années l’âge de la mère sera-t-il le triple de l’âge de René ?

Albert dépose ses 153 écus dans un coffre 3 × 3. Chaque lettre représente un nombre différent d’écus. Par exemple, le coffre B contient deux écus et le D 12 écus. Il doit y avoir le même nombre d’écus dans chaque rangée horizontale, verticale et diagonale.

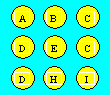
 Déterminez le montant d’argent par case.

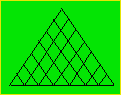
Dans cette figure, combien peut-on compter de triangles formés de six parties ?

Dans la grille, chaque lettre représente un nombre différent. Par exemple, N = 3. La somme des nombres de chaque rangée horizontale, verticale et diagonale doit être égale à 21.

Quelle est la valeur de MAP ?

Paulin possède six balles numérotées de 4 à 9. Il désire disposer ses balles en un triangle. La somme des numéros sur chaque côté doit être la même.

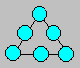
Déterminez la plus petite somme.

Jean est né le troisième jeudi du mois de mai 2009. Quel est le quantième de sa date de naissance ?

Chaque symbole représente un chiffre différent. La somme de chaque ligne est donnée à droite et celle de chaque colonne en bas.

Quelle est la valeur de ¨ ?

Chacun des chiffres s’écrit de la façon indiquée ci-dessous.

Quel est le plus petit nombre de trois chiffres qui utilise neuf trèfles ?

Le numéro civique de la maison de Marc est composé de deux chiffres. Si on soustrait 1 au numéro, le résultat est divisible par 2 et par 7. Si on soustrait 2 au numéro, le résultat est divisible par 5. Quel est le numéro de la maison de Marc ?

Dans cette grille, tracez une droite de façon à ce que la somme des nombres touchés soit égale à 18.

Déterminez le dernier chiffre de 247¹⁰⁰.

Renée place un dé sur chacune des cases d’un carré 3 × 3. Elle lit le nombre de points sur la face supérieure des dés. Il n’y a pas de 1. Le seul 6 est sur la case centrale de la dernière ligne.

Complétez la grille pour qu’il y ait 12 points sur chaque ligne, dans chaque colonne et dans chaque diagonale.

Solutions 1 à 50

Solutions 51 à 100

Solutions 101 à 150