*****************
Problems 51 to 100
*****************

In a hen house, there are 12 white, 12 black and 12 grey hens. There are 36 roosts. Twelve hens are in position.

Each of 24 other hens must be perched so that there are two hens of the same color in each horizontal, vertical and diagonal row. 

Determine the positions.

In a circular ground, Kelly places rows of flowers in straight line and plants a tree in each empty part. When there are three rows of flowers, she plants seven trees.

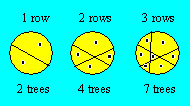
How many trees to the maximum will she plant if another row is added ?

In the diagram, there are six squares and 17 matches.

Remove four matches and obtain three squares.

Using the following clues, fill the grid so that the sum of numbers in each line, column and diagonal is the same.

Starting from J City, John wants to reach D City by passing through three other cities.

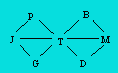
How many paths are possible ?

In the addition, replace four digits by 5 so that the sum remains 974.

How many squares of any size can you count in this grid 4 × 4 ?

Place signs + or - between certain digits of this number in order to obtain 14 like result.

Complete the first four numbers. The fifth number is formed with the missing digits.

Find the square.

Mary chooses a number. She makes the operations in this order : to multiply by 4, to add 4, to divide by 4 and to subtract 4.

What is the difference between the chosen number and the result ?

Find three 3-digit numbers.

They are formed by digits from 1 to 9.

The second number is twice the first.

The third is three times the first.

The last digit of the third number is 1.

Justin undertook to build a jigsaw puzzle. Each day, he doubled the number of pieces. After five days, he had placed half of his pieces.

Find the number of days during which Justin will have worked to build his puzzle.

Place signs + or - between certain digits of this number. The result must be 12.

Derek chooses three numbers smaller than 100.

He subtracts the middle number from the greatest.

He subtracts the smallest from the middle number.

He adds the two results.

He adds the smallest number.

What result will he obtain ?

The building below has 17 doors. Starting at point A, Lorena goes through every door only once and returns where she started.

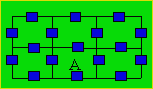
Draw a path.

June buys 90 tiles that measure one meter on each side. He places his tiles in a rectangle. Every side measures more than three meters. 

How many rectangles can have different measurements in whole values ?

Using only once the digits below, represent successively 1, 2, 3, 4, 5, 6, 7 and 8. The allowed operations are : +, –, ´ and ¸, as well as the square root.

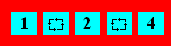
Divide the grid into five sections of same size but not necessarily of same shape. You must find one A and one B in each section.

Using four 3, represent successively 1, 2, 3, 4, 5 and 6. The allowed operations are : +, –, ´ and ¸.

Each letter represents a different digit.

E + V = DB               N + D = S               S + S = R                 N + R = E
L – V = N                  B – A = D              N + N + N + N = E

Decipher this expression.

Using five 4, represent successively 7, 8, 9, 10, 11 and 12. The allowed operations are : +, –, ´ and ¸, as well as the square root.

How many squares 3 ´ 3 can you count in this grid 6 × 8 ?

Using a balancing scale, James wants to weigh a 60 gram object. He must use four different weights, each one being twice the weight of the preceeding one. 

What are the different weights used by James ?

In the circles, write the numbers 4, 5, 6, 6, 7, 8, 9 and 10. The sum of two or three circles joined by a straight line must be equal to 16.

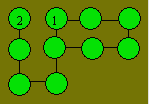
What is the greatest number that can be written with one 2 and one 6 ?

Draw seven straight lines to form four squares of the same size.

Albert planted decorative nails on 15 bricks. The number of nails is equal to the quantity of nails that is found on the two bricks just below. Albert wrote the number of nails on each brick, but somebody erased nine numbers.

Indicate the number of nails on the nine bricks.

The number 142 857 is curious. Indeed, 142 857 ´ 2 = 285 714, 142 857 ´ 3 = 428 571 and 142 857 ´ 4 = 571 428. 

Without calculating fully, find the product of 142 857 and 5.

How many numbers divisible by 4 can be formed with these four digits ?

You take the number 28. You make these operations in various orders : to add 4, to subtract 4, to multiply by 4, to divide by 4 and to extract the square root. The result is 5.

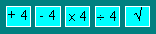
Give the order of the operations.

Stanley cut out a part of a calendar as below. He wishes to move the dates so that he obtains the same sum in each horizontal, vertical and diagonal row. The number 21 remains in position. The 14 and the 20 are each one in a corner.

Find an arrangement.

Find an equality of the form : A² + B² + C² = D² + E². The values of the letters are 2, 3, 4, 5 and 6.

A pawn moves diagonally on a board. It begins at point A and stops on the last horizontal row.

How many possible paths can it make ?

Calculate the difference between the square of 99 964 and the square of 99 963.

A gardener bought 154 flowers. He wants to arrange them in seven different blocks as below ; three blocks must contain 8, 27 and 31 flowers. The upper block contains 22 flowers. There are 66 flowers in each row of three blocks.

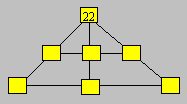
Determine the number of flowers in each block.

Find the number smaller than 100 that can be divided by the greatest quantity of numbers from 2 to 9.

Among the four expressions, which is the greatest : 2⁵, 3⁴, 4³ or 5² ?

Robert buys stamps for an amount of 148 cents. He wants the greatest number of 8-cent stamps and the rest in 7-cent stamps. 

How many 7-cent and 8-cent stamps will he receive ?

Daniel is nine years old. His mother is 37 years old. In how many years will the mother’s age be three times the Daniel's age ?

Albert deposited 153 cents in a safe that has 3 ´ 3 compartments. Each letter represents a different number. For example, the safe B contains two cents and D 12 cents. The number of cents must be the same in each horizontal, vertical and diagonal row.

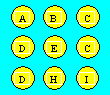
 Determine the amount of money in each compartment.

In this figure, how many triangles formed by six parts can you count ?

In the grid, each letter represents a different number. For example, N = 3. The sum of the numbers of each horizontal, vertical and diagonal row must be equal to 21.

What is the value of MAP ?

Paul possesses six balls numbered from 4 to 9. He arranges his balls in a triangle. The sum of the numbers on each side has to be the same.

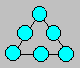
Find the smallest sum.

Paulin is born on the third Thursday of May 2009. What was the day of the month ?

Each symbol represents a different digit. The sum of each line is given on the right and that of each column at the bottom.

What is the value of  ¨  ?

Each digit is represented below with some clubs.

What is the smallest three-digit number that uses nine clubs ?

The civic number of Mark's house is composed of two digits. If we subtract 1 from the number, the result is divisible by 2 and by 7. If we subtract 2 from the number, the result is divisible by 5. 

What is the number of Mark's house ?

In this grid, trace a straight line so that the sum of numbers below the line is equal to 18.

Find the last digit of 247¹⁰⁰.

Helen places a die on each cell of a square 3 × 3. She reads the number of points on the superior face of the die. There is only one 6 and it is on the central box of the last line. There is no 1.

Fill in the grid so that there are 12 points in each line, in each column and in each diagonal.