*****************
Problems 101 to 150
*****************

Gabriel buys 182 tiles that measure one meter on each side. He places the tiles in a rectangle almost square. 

Find the measurements of the rectangle in whole values.

Draw six straight lines to form two squares of the same size.

In this figure, draw five squares of the same size without tracing straight lines horizontally or vertically.

Find a number that is a square and that remains a square if we add or subtract 120 from it.

Find the number of squares in this sequence : 1, 3, 5, 7, 9, 11, 13, …, 299.

Kate rented an apartment on the 45^th floor of a building of 85 floors on November 1^st 2008. She wanted to move twice a year : up five floors on March 1^st and down three floors on November 1^st. 

On which floor, will Kate live on April 1^st 2013 ?

On a rectangular board, Larry throws 84 darts. At the end, each line contains 28 darts and each column 21. The empty squares have respectively from 1 to 9 darts, except 7.

Indicate the number of darts per empty square.

What can be done with one 4 and one 5 ? Find at least four possibilities.

Each of the digits is represented below with some clubs.

What is the greatest number of three different digits that uses 10 clubs ?

Using four 3, represent successively 7, 8, 9, 10, 11 and 12. The allowed operations are : +, –, ´ and ¸, as well as the square root.

Each letter represents a different digit. For example, R = 2 and P = 4. The sum of numbers in each line, column and diagonal is equal to PB.

What is the value of PB ?

In the empty squares, write each of the numbers from 1 to 8 so that you obtain the horizontal and vertical results.

I am the smallest number that is divisible by the numbers from 1 to 9. Who am I ?

Bill has a rectangular ground. Its length is higher of 25 meters than the width. Bill wishes to divide its ground into 15 parts each one measuring 60 square meters. 

What is the length of the ground ?

This figure consists of eight balls and five rows of three balls each one.

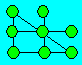
Using nine balls, form four rows of three balls each one.

In my school, there is a mathematics club. Its phone number is ABC-DEFG.

A is half of B.

B is smaller than C by one.

C added to D is an odd number.

D is half the sum of A and B.

E is C minus A.

F is C minus B.

G is the sum of A and B minus C.

What is the phone number of the club ?

Nine buses carry 234 passengers. At a particular moment, the nine buses have the same number of passengers in each horizontal, vertical and diagonal row. Moreover, the buses B and G have 39 and 31 passengers respectively.

What is the number of passengers on the other buses ?

Among the following expressions, which is the greatest : 8⁹ or 9⁸ ?

You take the number 40. You make these operations in various orders : to add 5, to subtract 5, to multiply by 5 and to divide by 5.

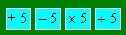
Find the smallest result.

In the board, each letter corresponds to a different digit. For example, M = 3 and G = 7. The sum of the numbers of each line is given on the right and that of each column at the bottom. When two letters are joined, they form a two-digit number.

What is the value of JP ?

A pawn moves diagonally on a rectangular board. It begins at point A and stops on the last row.

How many paths can it make ?

Marilyn decided to write the digits with balls.

What is the greatest odd number of two different digits that requires 10 balls ?

In this figure, Zachary wants to place each number from 3 to 11. He wrote the 5 and the 8.

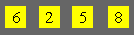
Write the other numbers. The sum of the numbers of the cells joined by a straight line must be equal to 21.

Examine carefully the numbers in the first three circles.

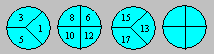
Complete the fourth circle.

A clothing store paid this advertising space in a newspaper. The cost of three articles is mentioned.

Find the cost of the other articles, since the total cost is of 108 euros in each horizontal, vertical and diagonal row.

Place signs + between some digits of this number. The sum must be 121.

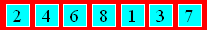
Represent 100 by successively using six 8, seven 8, eight 8, nine 8, ten 8, eleven 8 and twelve 8. The allowed operations are : +, –, ´ and ¸.

Raymond divided his field in 30 square pieces. He planted six trees, one by piece.

Determine the number of grounds 2 ´ 2 that have only one tree.

Gerry has a bag of balls. He sells a third of his bag and gives three balls. Again, he sells a third of the remaining balls and gives three balls. For the last time, he sells a third of the remaining balls and gives three balls. He has then seven balls in his bag. 

How many balls had Gerry at the beginning ?

In the grid, place numbers so that the sum in each line and in each column is 50.

Marilyn decided to write the digits with balls.

Find the smallest even number of two digits that requires 11 balls.

Henry chooses a two-digit number. He multiplies by 3, adds 12, divides by 3 and subtracts the chosen number. What is the result compared to the chosen number ?

Find the 15^th number of this sequence : 2, 5, 4, 7, 6, 9, 8, 11, ...

Martin bought 99 flowers. He wants to arrange them in six blocks. The three blocks of corners must contain 10, 12 and 17 flowers. The number of flowers must be the same in each row of three blocks.

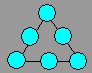
How many flowers did Martin plant in each block ?

In the diagram, there are six squares and 17 matches.

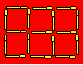
Remove six matches and obtain two rectangles.

Find two numbers the sum of squares of which is 274.

Peggy wants make a square carpet with 25 squares of same size. She has five red squares, five blue, five purple, five yellow and five grey. Eight squares have already their color.

Arrange the colors so that each one appears once in each horizontal, vertical and diagonal row.

Passing by the points of this figure, form six lozenges of same size.

In a box, Ann placed 15 tokens.

· 5 tokens marked 1 point

· 5 tokens marked 2 points

· 5 tokens marked 5 points

Remy wants nine tokens with a total of 17 points. What tokens will Remy receive ?

Cynthia owns four apartment buildings. The number on each one is composed of the same four digits whose the sum is 20. The sum of the four numbers is 22 220.

Find the numbers.

Four times the sum of a two-digit number is equal to this number. Twice the product of the two digits is also equal to this number. What is this number ?

In the addition, each letter represents a different digit. For example, R = 2 and M = 8.

What is the value of POWER ?

Pascal traces a continuous line from a point of the circumference to another. Thus he divides the circle in five parts.

Trace two other straight lines continuously for having a maximum of parts. What is this maximum ?

Among the six numbers, there is only one that is not a square.

Find this number without extracting any square root.

This figure consists of eight balls and five rows of three balls each one.

Using seven balls, form four rows of three balls each one.

Each letter represents a different digit. For example, R = 8.

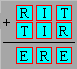
What is the value of RITE ?

The divisors of 16 are 1, 2, 4, 8 and 16. The sum of these divisors is 31. Find another number where the sum of the divisors is also 31.

In the four operations, each letter represents a different digit.

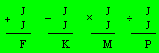
Quelle est la valeur de FKMP ?

In a village, a new number system was adopted. There are only two digits, 0 and 1. The table of equivalence is as follows :

There are 11 ´ 111 ´ 1111 inhabitants in this village. What is that number in our system ?

In this series of six dominos, the upper row contains 20 points and the bottom row 12 points.

Move two dominos in order to obtain the same number of points per row.