This is the third book published by Récréomath.

Mathematical 
Amusements

Par Charles-É. Jean

This edition includes 200 problems and their solution. The French version is published.

Solutions 1 to 50

Solutions 101 to 150

***************
Solutions 51 to 100
***************

Solution 51. Here is a distribution of the hens :

Solution 52. The last row of the flowers must cut the rows already existing. For four rows, we will have 7 + 4 = 11 trees.

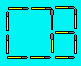
Solution 53. Here are three squares :

Solution 54. E = 19, G = 17, C = 21 and I = 29. The sum of the numbers in each row is 57. The filled board is :

Solution 55. There are three possible paths : (T, B, M), (P, T, M) and (G, T, M).

Solution 56. We replace the 3 and the 7 of the column of the units, also the 2 and the 8 of the column of the tens.

Solution 57. We can count 30 squares.

Solution 58. We can write : 4 + 56 – 12 – 34 = 14.

Solution 59. The numbers divisible by 7, 11, 12 and 13 are respectively 8568, 6226, 5172 and 5577. Together we put the digits 5, 2, 2 and 7. The square is 7225.

Solution 60. The difference is 3.

Solution 61. The numbers are 327, 654 and 981.

Solution 62. Justin worked for six days. Indeed, after five days he had made the half jigsaw.

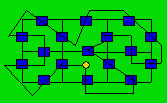
Solution 63. We can write : 123 + 45 – 67 – 89 = 12.

Solution 64. The result is always the greatest number.

Solution 65. A path is :

Solution 66. We can have three rectangles. The measurements are : 5 ´ 18, 6 ´ 15 and 9 ´ 10.

Solution 67. Here is a way of representing each number from 1 to 8 :

Solution 68. Since there are 25 boxes, each part contains five boxes. The dividing is :

Solution 69. Here is a way of representing each number from 1 to 6 :

Other examples are given for 1 :

Solution 70. D = 1, N = 2, S = 3, A = 4, B = 5, R = 6, V = 7, E = 8 and L = 9. The expression is : A VERNAL BALLAD.

Solution 71. Here is a way of representing each number from 7 to 12 :

Solution 72. We can count 24 squares 3 ´ 3.

Solution 73. We suppose that the denomination of the smaller weight is of one gram. The three other denominations will be of two, four and eight grams. We can weigh an object of 15 grams. Each weight must be four times heavier. The weights are of 4, 8, 16 and 32 grams.

Solution 74. The two-number combinations that have a sum of 16 are : (6, 10) and (7, 9). The three-number combinations that have a sum of 16 are : (1, 5, 10), (1, 6, 9), (1, 7, 8), (2, 4, 10), (2, 5, 9), (2, 6, 8), (4, 5, 7) and (4, 6, 6). An arrangement of the numbers is :

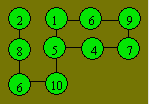
Solution 75. The greatest number is 2⁶ = 64.

Solution 76. A figure is :

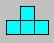
Solution 77. An arrangement is :

Solution 78. The digits 1, 4, 2, 8, 5 and 7 follow each other in a circular way. The last digit is 5. The product is 714 285.

Solution 79. A number is divisible by 4 when the number formed by the last two digits is divisible by 4. There are three cases : 24, 32 and 52. We can form six numbers : 3452, 3524, 4352, 4532, 5324 and 5432.

Solution 80. There are two ways. In order, the operations are : (´ , +, ¸, - , Ö ) or (- , ´ , +, ¸, Ö ).

Solution 81. The total sum of numbers is 189. The sum for each row is 63. Here is an arrangement :

Solution 82. The equality is : 2² + 4² + 5² = 3² + 6².

Solution 83. There are 12 possible paths.

Solution 84. We make : 99 964 + 99 963 = 199 927. The difference of two squares is 199 927.

Solution 85. An arrangement of the flowers is :

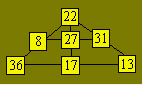
Solution 86. The number is 72. It is divisible by 2, 3, 4, 6, 8 and 9.

Solution 87. The greatest expression is 3⁴.

Solution 88. Robert bought 15 eight-cent stamps and 4 seven-cent stamps.

Solution 89. In five years, Daniel will be 14 years old and his mother 42 years old.

Solution 90. Albert put 51 cents by row. The amount by compartment is :

Solution 91. We can count five triangles.

Solution 92. A = 9, since N = 3 and A + A + N = 21. The value of MAP is 195.

Solution 93. The total sum of the numbers is 39. The smallest sum is 18.

Solution 94. The day is 21.

Solution 95. We add up the sums of each line or of each column. We obtain 40. The value of ¨ is 4.

Solution 96. This number is 104.

Solution 97. When we subtract 1 to this number, the result is divisible by 14. The multiples of 14 are : 14, 28, 42, 56, 70, 84 and 98. When we add up 1, we obtain : 15, 29, 43, 57, 71, 85 and 99. The civic number is 57.

Solution 98. We trace the line on 7, 2 and 9.

Solution 99. Depending on the power of numbers, we write the last digit in this board.

The last digit is 1 for the powers 4, 8, 12… The last digit of 247¹⁰⁰ is 1.

Solution 100. The filled square is :

Solutions 1 to 50

Solutions 101 to 150