This is the third book published by Récréomath.

Mathematical 
Amusements

Par Charles-É. Jean

This edition includes 200 problems and their solution. The French version is published.

Solutions 51 to 100

Solutions 101 to 150

***************
Solutions 1 to 50
***************

Solution 1. Here are four squares :

Solution 2. There are successively 25, 26, 27, 28, 29 horses.

Solution 3. Here is a filled grid :

Solution 4. The value of E is 7.

Solution 5. An arrangement of the numbers is :

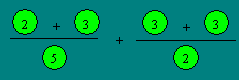
Solution 6. We make : 1068 – 239 – 457 = 372. We divide 372 by 3. The result is 124. The missing numbers are 124 and 248.

Solution 7. The sum of the numbers from 1 to 25 is 325. The sum of the numbers of each line or each column is 325/5 = 65.

Solution 8. Here is a path :

Solution 9. The possible path is : J, P, T, M.

Solution 10. We make : 974 – 602 = 372. We replace the 3 of the units, the 8 of the tens and the 4 of the hundreds.

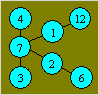
Solution 11. An arrangement of the numbers is :

Solution 12. The best path is : B, A, C, B. Martin delivers successively 22, 25, 18 and 22 : in all 87 automobiles.

Solution 13. Here is an arrangement :

Solution 14. A filled grid is :

Solution 15. The distribution of rabbits is :

Solution 16. The multiplication is 999 ´ 29 = 28 971.

Solution 17. The three-number combinations that have a sum of 18 are : (3, 5, 10), (3, 6, 9), (3, 7, 8), (4, 5, 9), (4, 6, 8) and (5, 6, 7). An arrangement is :

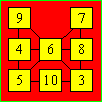
Solution 18. The equality is 6439 + 8643 = 15 082. MATH corresponds to 6 439.

Solution 19. No, since 2⁹⁹ is not divisible by 3.

Solution 20. The value of ( is 5.

Solution 21. We make : 974 – 909 = 65. We replace the 7 of the column of the units and the 8 of the column of the tens.

Solution 22. We count 10 lozenges.

Solution 23. The three-number combinations that have a sum of 16 are : (1, 4, 11), (1, 5, 10), (1, 6, 9), (1, 7, 8), (2, 3, 11), (2, 4, 10), (2, 5, 9), (2, 6, 8), (3, 4, 9), (3, 5, 8), (3, 6, 7) and (4, 5, 7). An arrangement is :

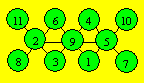
Solution 24. The greatest result is 60. We can obtain it in two ways. In order, the operations are : (- , ¸ , +, ´ ) or (¸ , +, ´ , - ).

Solution 25. Here is an arrangement of the numbers :

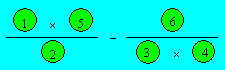
Solution 26. The number for each word is :

The word is EAGLES.

Solution 27. There are 21 horses per row.

Solution 28. For example, we take 58. The sum of the digits is 13. Then, A = 13. We make : 58 + 85 = 143 and 143 ÷ 11 = 13. Then, B = 13 and B – A = 0. We test some other numbers. The difference is always 0.

Solution 29. The four numbers are : 5768, 7568, 7856 and 8576.

Solution 30. The numbers can be arranged thus :

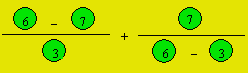
Solution 31. The divisors of 90 smaller than 16 are 1, 2, 3, 5, 6, 9, 10 and 15. An arrangement of the numbers is :

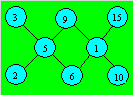
Solution 32. We make : 1068 – (2 × 258) = 552. The square root of 552 is between 23 and 24. The missing numbers are 23 and 529.

Solution 33. We reverse the second and the third domino.

Solution 34. Three numbers are possible : 1536, 4836 and 5936.

Solution 35. Magic squares reveal the intrinsic harmony and symmetry of numbers.

Solution 36. Here is the filled grid :

Solution 37. We divise the given number by 12. The remainder of the division of 141 by 12 is 9. If the remainder is even, it is the rank of the month (if the remainder is 0, it is December). If the remainder is odd, we add or subtract 6. The month is March.

Solution 38. An arrangement of the numbers is :

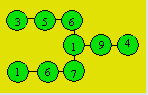
Solution 39. An equality is : 15 + 34 + 2 = 51.

Solution 40. The filled board is :

Solution 41. Instead of juggling with the numbers, the farmer juggled with the balls.

Solution 42. We find 12 numbers divisible by 2.

Solution 43. An arrangement is :

Solution 44. We decompose 224 in two factors. The even factors are : (2, 112), (4, 56), (8, 28) and (14, 16). We obtain four pairs : 57 and 55, 18 and 10, 30 and 26, 15 and 1.

Solution 45. The divisors of 120 smaller than 16 are 1, 2, 3, 4, 5, 6, 8, 10, 12, 15. The three-number combinations that have a product of 120 are : (1, 8, 15), (1, 10, 12), (2, 4, 15), (2, 5, 12), (2, 6, 10), (3, 4, 10), (3, 5, 8) and (4, 5, 6). An arrangement of the numbers is :

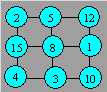
Solution 46. Here is a path for the knight :

Solution 47. The white circle weighs eight grams, the circle with a point two grams, the circle with a line 16 grams and the circle with a cross six grams.

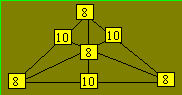
Solution 48. The number of employees in each department is :

Solution 49. Since D + B = B, D = 0. Since A + A = ED, A = 5 and E = 1. Since A × B = ED, then B = 2 and F = 7. The number that corresponds to FADE is 7 501.

Solution 50. Here is a way of representing each number from 1 to 6 :

Solutions 51 to 100

Solutions 101 to 150