|
***************
Problems
151 to 200
***************
151
In the diagram, there
are six squares and 17 matches.
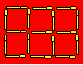
Remove five matches and obtain
three squares.
152
How many squares 2
× 2 can you count in this grid ? Each square must contain exactly one
circle and two white squares.
153
Andrew possesses
eight balls numbered from 1 to 8. How many groups of four balls can have a sum
of 16 ?
154
The sum of two
numbers A and B is 19. If we add the double of A and the triple of B, the result
is 50. Which is the value of A and B ?
155
Find the number of
squares in this sequence : 3, 7, 11, 15, 19, 23, ..., 999.
156
Place a sign +, –,
´ or ÷ between the digits of this number in order
to obtain 7 like result.
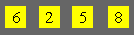
157
In each square, we
can read a number.
|
5 |
7 |
3 |
8 |
2 |
|
3 |
9 |
2 |
4 |
3 |
|
2 |
5 |
7 |
4 |
9 |
|
6 |
4 |
3 |
5 |
3 |
|
4 |
5 |
6 |
7 |
6 |
Find the number of rectangles 2
´ 3 where the sum is less than 26.
158
You choose two
numbers. You add, subtract, multiply and divide them. At the end, you add these
four results. The greatest selected number is 77.
Find the smallest number
except for 1.
159
In this grid, choose four couples of
numbers, a couple by line.
|
14 |
3 |
4 |
17 |
|
6 |
11 |
12 |
9 |
|
10 |
7 |
8 |
13 |
|
2 |
15 |
16 |
5 |
Invert the numbers of each couple
so that the sum is 38 in each column. The sum of the numbers of each line does
not change.
160
Draw one 4 and one 3
to form 43. Remove two segments and move another to obtain the smallest possible
number.

Find this
number.
161
In the five empty
squares, write each digit from 3 to 7 so that the sum is 144.
162
In the grid, find the number of squares
3 ´ 3 that have only one club.
163
In this
grid, write
some numbers from 1 to 6. The numbers must be different in each line and in each
column.
164
On December 1, 2008
was one Monday. Mary is born on March 8, 2009. Find the day of the week of the
birth of Mary.
165
How many squares 3
´ 3 can you count in a grid 5 × 5 ?
166
Elizabeth chooses a
number. She makes the operations in this order : to add 12, to multiply by 3, to
subtract 6 and to divide by 3. The result is 46.
Find the chosen
number.
167
Place a sign +, -
or ´ between the numbers so that the equality is
true.
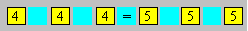
168
Peter has 32 years
and Mary 29 years. When Pierre did he have the double of the age of Mary ?
169
Robert buys stamps
for an amount of 234 cents. He wants the same number of stamps of six cents and
seven cents. Find the number of stamps of each value.
170
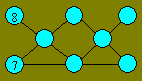
In the
circles, write
each of the numbers from 1 to 6 so that the sum is 13 in each row of three
circles.
171
The age of Adam is
triple of that of Blondie. The sum of the ages is 56. Which is the age of
Blondie ?
172
In the empty squares,
write each of the numbers from 1 to 6.
Find the smallest
sum.
173
How many squares 3
´ 3 can you count in a grid 5 × 6 ?
174
Adelia is born
Tuesday on February 29, 2000. Which day of the week was on February 29, 2001 ?
175
Marilyn decided to
write the digits with balls.

What is the smallest number of two
digits that requires 11 balls ?
176
Find
the 19th number of this sequence : 1, 3, 5, 4, 6, 8, 7, 9, 11, 10 …
177
How many squares 4
´ 4 can you count in a grid 8 × 8 ?
178
Draw six straight
lines to form four squares of the same size.
179
A
twelfth of a brick weighs the quarter of one kilogram. Determine the weight of
four bricks.
180
In the six empty
squares, write 2, 4, 5, 6, 8 and 9 so that the addition is true.
181
Find
the number of squares in this sequence : 3, 6, 9, 12, 15, 18, 21, …, 999.
182
Brooke rented an
apartment on the 75e floor of a building of 85 floors on July 1st
2007. She wanted to move twice a year : up five floors on January 1st
and down three floors on July 1st.
In which year will she remain on
the last floor of the building ?
183
Brice is born on
April 25. How many days did he live on June 25 of the same year ?
184
In the nine empty squares, write 2, 4,
5, 6, 8 and 9 so that the equalities are true.
185
In the
circles, write
each of the numbers from 1 to 6 so that the sum is 16 in each row of three
circles.
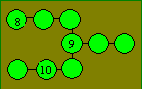
186
You take the number
51. You make these operations in various orders : to add 3, to subtract 3, to
multiply by 3, to divide by 3 and to extract the square root.
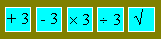
The result is 15. Give the order of
the operations.
187
Place signs + between
certain digits of this number in order to obtain 1066 like result.

188
In each square, we
can read a number.
|
5 |
7 |
3 |
8 |
2 |
|
3 |
9 |
2 |
4 |
3 |
|
2 |
5 |
7 |
4 |
9 |
|
6 |
4 |
3 |
5 |
3 |
|
4 |
5 |
6 |
7 |
6 |
Find the number of squares 2
´ 2 where the sum is more than 21.
189
Billy has a bag of
balls. He gives three balls. He sells a third of the remaining balls and gives
three balls. Again, he sells a third of the remaining balls and gives three
balls. He has then 11 balls in his bag.
How many balls had Billy at the
beginning ?
190
Beatrice chooses a
number. She makes the operations in this order : to add 3, to multiply by 4, to
subtract 12 and to multiply by ½.
Which is the relationship between the result
and the chosen number ?
191
Find the 14th
number of this sequence : 4, 3, 7, 6, 13, 12, 25, 24, 49, 48, 97, 96, ...
192
In a box, Brenda placed 15
tokens.
· 5 tokens marked 1 point
· 5 tokens marked 2 points
· 5 tokens marked 5 points
Benjamin wants six tokens with a total of 17 points. What
tokens will Benjamin receive ?
193
Draw six straight
lines to form three triangles of the same size.
194
Which number is the
greatest : 98 763 ´
98 765 or the square of 98
764 ?
195
This figure consists
of eight balls and four rows of three balls each one.
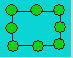
Move one ball in order to obtain
five rows of three balls each one.
196
In the addition, each letter represents
a different digit. For example, A = 8 and P = 4.
Which is the value of R ?
197
Draw one 8 and one 5
to form 85. Remove three segments to obtain the greatest possible number.

Which is this number ?
198
Using these
numbers,
represent 109. The allowed operations are : +, –, ´
and ¸.

199
Draw six straight
lines to form four triangles of the same size.
200
Adele places eight coins in a circular
way. She removes a first coin and successively the third coin. She continues
thus until a single coin remains.

What coin will be the last ?
|
![]()
![]()